 Technology peripherals
Technology peripherals
 AI
AI
 roll! MIT Poisson flow generation model beats diffusion model, taking into account both quality and speed
roll! MIT Poisson flow generation model beats diffusion model, taking into account both quality and speed
roll! MIT Poisson flow generation model beats diffusion model, taking into account both quality and speed
Introduction
The diffusion model was originally derived from thermodynamics in physics, but recently it has shone in the field of artificial intelligence. What other physical theories can promote the development of generative model research? Recently, researchers from MIT were inspired by high-dimensional electromagnetic theory and proposed a generative model called Poisson Flow. Theoretically, this model has intuitive images and rigorous theory; experimentally, it is often better than the diffusion model in terms of generation quality, generation speed and robustness. This article has been accepted by NeurIPS 2022.

- ##Paper address: https://arxiv.org/abs/2209.11178
- Code address: https://github.com/Newbeeer/Poisson_flow
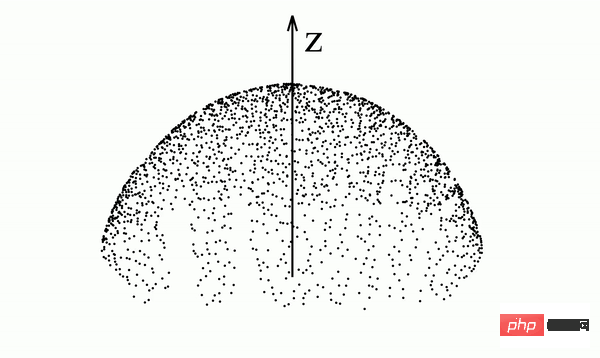
Inspired by electrostatic mechanics, the researchers proposed a new generative model called Poisson flow model (Poisson Flow Generative Models, or PFGM). Intuitively, this research can regard the N-dimensional data points as a group of positive charges on the z=0 plane, a new dimension in the N 1-dimensional space. They generate an electric field in the high-dimensional space. Starting from the z=0 plane and moving outward along the electric field lines they generate, the study was able to deliver the sample to a hemisphere (as shown in Figure 1). The direction of these electric field lines corresponds to the gradient of the solution to the Poisson Equation in high-dimensional space. The researchers proved that when the radius of the hemisphere is large enough, the electric field lines can transform the charge distribution (that is, the data distribution) on the z=0 plane into a uniform distribution on the hemisphere (Figure 2).
PFGM takes advantage of the reversibility of electric field lines to generate data distribution on the z=0 plane: first, researchers sample uniformly on a large hemisphere, and then let the sample follow the electric field lines Move from the sphere to the z=0 plane to generate data. Since motion along electric field lines can be described by an ordinary differential equation (ODE), in actual sampling researchers only need to solve an ODE that is determined by the direction of the electric field lines. Through an electric field, PFGM converts a simple distribution on a sphere into a complex data distribution. From this perspective, PFGM can be considered as a continuous normalizing flow (Normalizing Flow).
In the image generation experiment, PFGM is currently the best performing standardized flow model on the standard data set CIFAR-10, achieving It achieved an FID score (a measure of picture quality) of 2.35. The researchers also demonstrated other uses of PFGM, such as its ability to calculate image likelihood, perform image editing, and scale to high-resolution image data sets. In addition, researchers found that PFGM has three advantages over the recently popular diffusion models: (1) In On the same network structure, the sample quality generated by PFGM's ODE is much better than that of the diffusion model's ODE; (2) While the quality of the SDE (stochastic differential equation) generated by the diffusion model is similar, the ODE of PFGM reaches 10 times - 20 times acceleration;
(3) PFGM is more robust than the diffusion model on network structures with weaker expressive capabilities.
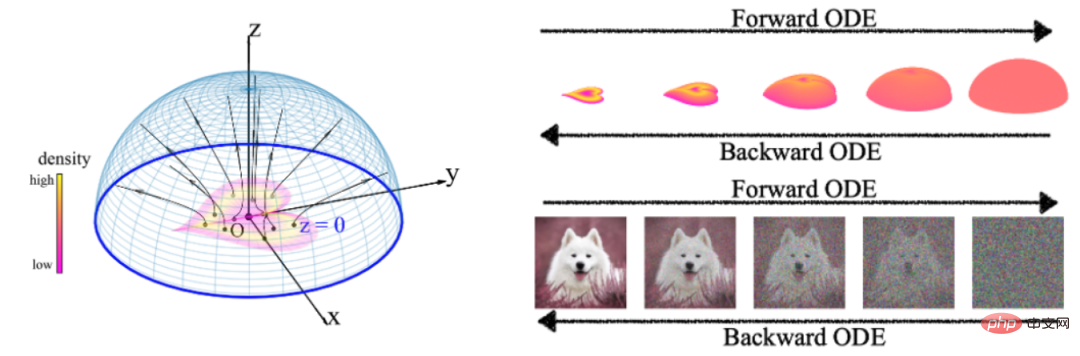 ##Figure 2: Left: the trajectory of the Poisson field in three dimensions; right: forward ODE and reverse ODE using PFGM on the image
##Figure 2: Left: the trajectory of the Poisson field in three dimensions; right: forward ODE and reverse ODE using PFGM on the image
Notice that the above process embeds N-dimensional data into N 1-dimensional (extra z-dimensional) space. In order to facilitate the distinction, researchers use x and where Electric Field The trajectory of the line (see Figure 2) can be described by the following ODE: In the following theorem, the researchers proved the above ODE definition It represents a bijection of the uniform distribution on a high-dimensional hemisphere and the data distribution on the z=0 plane. This conclusion is the same as the intuition in Figures 1 and 2: the data distribution can be restored through electric field lines. Training of PFGM Given a data distribution The data set The electric field line gradient is the learning target. This study uses the perturb function to select points in the space, and the square loss function allows the neural network Sampling of PFGM After learning the normalization to learn the normalized electric field line gradient in the space, the data distribution can be sampled through the following ODE: This ODE gradually moves the sample from the large sphere along the electric field lines to the z=0 plane by reducing z. In addition, this study proposes to project the uniform distribution on a large sphere onto a certain z-plane to facilitate ODE simulations and further accelerate sampling through variable substitution. Please refer to Section 3.3 of the article for specific steps. In Table 1, this study uses the standard dataset CIFAR-10 to evaluate different models. On this dataset, PFGM is the best performing reversible normalized flow model, achieving an FID score of 2.35. PFGM performs better than the diffusion model using the same network structure (DDPM /DDPM deep). The researchers also observed that while the SDE (stochastic differential equation) generation quality of the diffusion model was similar, PFGM achieved an acceleration of 10 times - 20 times, better balancing the generation quality and speed. In addition, researchers found that PFGM is more robust than diffusion models on less expressive network structures, and is still better than diffusion models under the same conditions on higher-dimensional data sets. Please see the experimental section of the article for details. In Figure 3, the study visualizes the process of PFGM generating images. Table 1: Sample quality (FID, Inception) and number of sampling steps (NFE) on CIFAR-10 data #Figure 3: Sampling process of PFGM on CIFAR-10, CelebA 64x64, LSUN bedroom 256x256 This study proposed a Poisson-based The generative model PFGM of Eq. This model predicts the normalized electric field line gradients in an extended space of N 1 dimensions and is sampled by the corresponding ODEs of the electric field lines. In experiments, the model studied in this study is currently the best standardized flow model, and has achieved better generation effects and faster sampling speeds than the diffusion model on the same network structure. The sampling process of PFGM is more robust to noise and can also be extended to higher dimensional data sets. Researchers expect PFGM to also perform well in other application areas, such as molecule generation and 3D data generation. Method Overview
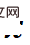 to represent N-dimensional data and N 1 dimensions. In order to obtain the above-mentioned high-dimensional electric field lines, the following Poisson equation needs to be solved:
to represent N-dimensional data and N 1 dimensions. In order to obtain the above-mentioned high-dimensional electric field lines, the following Poisson equation needs to be solved: 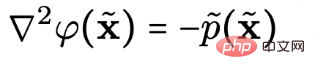
 is located z=0 is the data distribution to be generated on the plane;
is located z=0 is the data distribution to be generated on the plane;  is the potential function, which is the goal of the researcher's solution. Since only the direction of the electric field lines needed to be known, the researchers derived the analytical form of the gradient of the electric field lines (the gradient of the potential function):
is the potential function, which is the goal of the researcher's solution. Since only the direction of the electric field lines needed to be known, the researchers derived the analytical form of the gradient of the electric field lines (the gradient of the potential function): 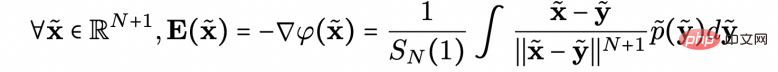


 was sampled. The researchers used the electric field line gradient corresponding to the data set to approximate the electric field line gradient corresponding to the data distribution:
was sampled. The researchers used the electric field line gradient corresponding to the data set to approximate the electric field line gradient corresponding to the data distribution: 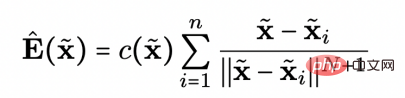
 to learn the normalized electric field line gradient## in the space.
to learn the normalized electric field line gradient## in the space.  #, the specific algorithm is as follows:
#, the specific algorithm is as follows: 
Experimental results




The above is the detailed content of roll! MIT Poisson flow generation model beats diffusion model, taking into account both quality and speed. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1377
1377
 52
52
 The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
May 07, 2024 pm 04:13 PM
The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
May 07, 2024 pm 04:13 PM
Imagine an artificial intelligence model that not only has the ability to surpass traditional computing, but also achieves more efficient performance at a lower cost. This is not science fiction, DeepSeek-V2[1], the world’s most powerful open source MoE model is here. DeepSeek-V2 is a powerful mixture of experts (MoE) language model with the characteristics of economical training and efficient inference. It consists of 236B parameters, 21B of which are used to activate each marker. Compared with DeepSeek67B, DeepSeek-V2 has stronger performance, while saving 42.5% of training costs, reducing KV cache by 93.3%, and increasing the maximum generation throughput to 5.76 times. DeepSeek is a company exploring general artificial intelligence
 AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI is indeed changing mathematics. Recently, Tao Zhexuan, who has been paying close attention to this issue, forwarded the latest issue of "Bulletin of the American Mathematical Society" (Bulletin of the American Mathematical Society). Focusing on the topic "Will machines change mathematics?", many mathematicians expressed their opinions. The whole process was full of sparks, hardcore and exciting. The author has a strong lineup, including Fields Medal winner Akshay Venkatesh, Chinese mathematician Zheng Lejun, NYU computer scientist Ernest Davis and many other well-known scholars in the industry. The world of AI has changed dramatically. You know, many of these articles were submitted a year ago.
 Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
Apr 18, 2024 pm 07:58 PM
Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas officially enters the era of electric robots! Yesterday, the hydraulic Atlas just "tearfully" withdrew from the stage of history. Today, Boston Dynamics announced that the electric Atlas is on the job. It seems that in the field of commercial humanoid robots, Boston Dynamics is determined to compete with Tesla. After the new video was released, it had already been viewed by more than one million people in just ten hours. The old people leave and new roles appear. This is a historical necessity. There is no doubt that this year is the explosive year of humanoid robots. Netizens commented: The advancement of robots has made this year's opening ceremony look like a human, and the degree of freedom is far greater than that of humans. But is this really not a horror movie? At the beginning of the video, Atlas is lying calmly on the ground, seemingly on his back. What follows is jaw-dropping
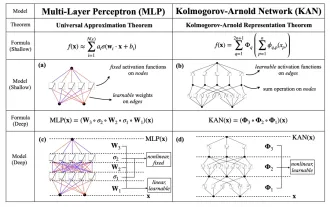 KAN, which replaces MLP, has been extended to convolution by open source projects
Jun 01, 2024 pm 10:03 PM
KAN, which replaces MLP, has been extended to convolution by open source projects
Jun 01, 2024 pm 10:03 PM
Earlier this month, researchers from MIT and other institutions proposed a very promising alternative to MLP - KAN. KAN outperforms MLP in terms of accuracy and interpretability. And it can outperform MLP running with a larger number of parameters with a very small number of parameters. For example, the authors stated that they used KAN to reproduce DeepMind's results with a smaller network and a higher degree of automation. Specifically, DeepMind's MLP has about 300,000 parameters, while KAN only has about 200 parameters. KAN has a strong mathematical foundation like MLP. MLP is based on the universal approximation theorem, while KAN is based on the Kolmogorov-Arnold representation theorem. As shown in the figure below, KAN has
 Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
Apr 01, 2024 pm 07:46 PM
Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
Apr 01, 2024 pm 07:46 PM
The performance of JAX, promoted by Google, has surpassed that of Pytorch and TensorFlow in recent benchmark tests, ranking first in 7 indicators. And the test was not done on the TPU with the best JAX performance. Although among developers, Pytorch is still more popular than Tensorflow. But in the future, perhaps more large models will be trained and run based on the JAX platform. Models Recently, the Keras team benchmarked three backends (TensorFlow, JAX, PyTorch) with the native PyTorch implementation and Keras2 with TensorFlow. First, they select a set of mainstream
 Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!
May 06, 2024 pm 04:13 PM
Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!
May 06, 2024 pm 04:13 PM
The latest video of Tesla's robot Optimus is released, and it can already work in the factory. At normal speed, it sorts batteries (Tesla's 4680 batteries) like this: The official also released what it looks like at 20x speed - on a small "workstation", picking and picking and picking: This time it is released One of the highlights of the video is that Optimus completes this work in the factory, completely autonomously, without human intervention throughout the process. And from the perspective of Optimus, it can also pick up and place the crooked battery, focusing on automatic error correction: Regarding Optimus's hand, NVIDIA scientist Jim Fan gave a high evaluation: Optimus's hand is the world's five-fingered robot. One of the most dexterous. Its hands are not only tactile
 FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
Target detection is a relatively mature problem in autonomous driving systems, among which pedestrian detection is one of the earliest algorithms to be deployed. Very comprehensive research has been carried out in most papers. However, distance perception using fisheye cameras for surround view is relatively less studied. Due to large radial distortion, standard bounding box representation is difficult to implement in fisheye cameras. To alleviate the above description, we explore extended bounding box, ellipse, and general polygon designs into polar/angular representations and define an instance segmentation mIOU metric to analyze these representations. The proposed model fisheyeDetNet with polygonal shape outperforms other models and simultaneously achieves 49.5% mAP on the Valeo fisheye camera dataset for autonomous driving
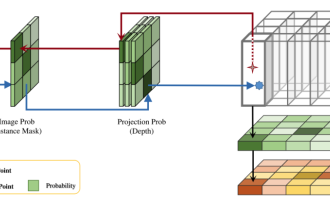 DualBEV: significantly surpassing BEVFormer and BEVDet4D, open the book!
Mar 21, 2024 pm 05:21 PM
DualBEV: significantly surpassing BEVFormer and BEVDet4D, open the book!
Mar 21, 2024 pm 05:21 PM
This paper explores the problem of accurately detecting objects from different viewing angles (such as perspective and bird's-eye view) in autonomous driving, especially how to effectively transform features from perspective (PV) to bird's-eye view (BEV) space. Transformation is implemented via the Visual Transformation (VT) module. Existing methods are broadly divided into two strategies: 2D to 3D and 3D to 2D conversion. 2D-to-3D methods improve dense 2D features by predicting depth probabilities, but the inherent uncertainty of depth predictions, especially in distant regions, may introduce inaccuracies. While 3D to 2D methods usually use 3D queries to sample 2D features and learn the attention weights of the correspondence between 3D and 2D features through a Transformer, which increases the computational and deployment time.



