Use Python to make a house price prediction gadget!

Hello, everyone.
This is a case of housing price prediction, which comes from the Kaggle website. It is the first competition question for many algorithm beginners.
This case has a complete process for solving machine learning problems, including EDA, feature engineering, model training, model fusion, etc.
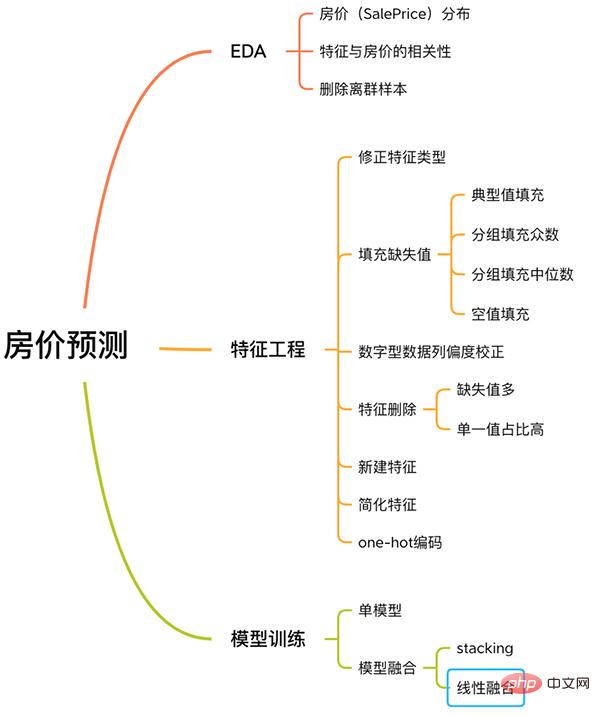
House Price Prediction Process
Follow me and learn about this case.
No long words, no redundant code, just simple explanations.
1. EDA
The purpose of Exploratory Data Analysis (EDA) is to give us a full understanding of the data set. At this step, the content we explore is as follows:

train = pd.read_csv('./data/train.csv')
test = pd.read_csv('./data/test.csv')
Copy after login
train = pd.read_csv('./data/train.csv')
test = pd.read_csv('./data/test.csv')

sns.distplot(train['SalePrice']);
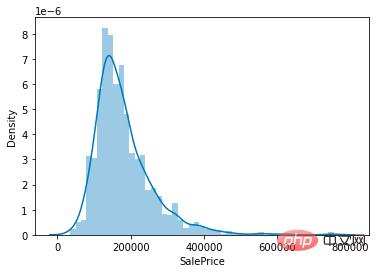
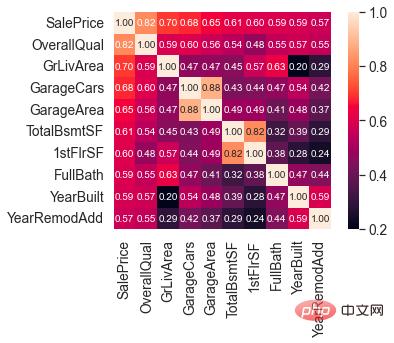
# 计算列之间相关性
corrmat = train.corr()
# 取 top10
k = 10
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
# 绘图
cm = np.corrcoef(train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
# 获取数值型特征 numeric_features = train.dtypes[train.dtypes != 'object'].index # 计算每个特征的离群样本 for feature in numeric_features: outs = detect_outliers(train[feature], train['SalePrice'],top=5, plot=False) all_outliers.extend(outs) # 输出离群次数最多的样本 print(Counter(all_outliers).most_common()) # 剔除离群样本 train = train.drop(train.index[outliers])
y = train.SalePrice.reset_index(drop=True) train_features = train.drop(['SalePrice'], axis=1) test_features = test features = pd.concat([train_features, test_features]).reset_index(drop=True)
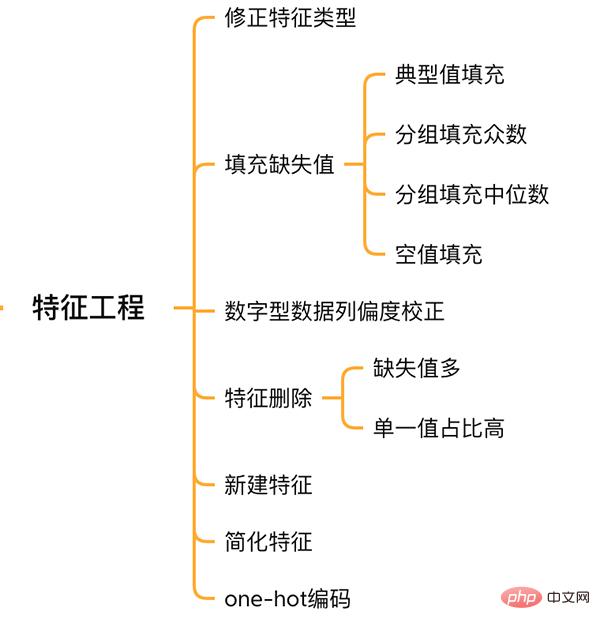 ##Feature Engineering
##Feature Engineering
2.1 Correction feature type
MSSubClass (house type), YrSold (Sales year) and MoSold (Sales month) are categorical features, but they are represented by numbers, and they need to be converted into text features.
features['MSSubClass'] = features['MSSubClass'].apply(str) features['YrSold'] = features['YrSold'].astype(str) features['MoSold'] = features['MoSold'].astype(str)
2.2 Filling missing values in features
There is no unified standard for filling missing values. It is necessary to decide how to fill in based on different features.
# Functional:文档提供了典型值 Typ
features['Functional'] = features['Functional'].fillna('Typ') #Typ 是典型值
# 分组填充需要按照相似的特征分组,取众数或中位数
# MSZoning(房屋区域)按照 MSSubClass(房屋)类型分组填充众数
features['MSZoning'] = features.groupby('MSSubClass')['MSZoning'].transform(lambda x: x.fillna(x.mode()[0]))
#LotFrontage(到接到举例)按Neighborhood分组填充中位数
features['LotFrontage'] = features.groupby('Neighborhood')['LotFrontage'].transform(lambda x: x.fillna(x.median()))
# 车库相关的数值型特征,空代表无,使用0填充空值。
for col in ('GarageYrBlt', 'GarageArea', 'GarageCars'):
features[col] = features[col].fillna(0)
2.3 Skewness Correction
Similar to exploring the SalePrice column, features with high skewness are smoothed.
# skew()方法,计算特征的偏度(skewness)。 skew_features = features[numeric_features].apply(lambda x: skew(x)).sort_values(ascending=False) # 取偏度大于 0.15 的特征 high_skew = skew_features[skew_features > 0.15] skew_index = high_skew.index # 处理高偏度特征,将其转化为正态分布,也可以使用简单的log变换 for i in skew_index: features[i] = boxcox1p(features[i], boxcox_normmax(features[i] + 1))
2.4 Feature deletion and addition
Features that are almost all missing values or have a high proportion of single values (99.94%) can be deleted directly.
features = features.drop(['Utilities', 'Street', 'PoolQC',], axis=1)
At the same time, multiple features can be fused to generate new features.
Sometimes it is difficult for the model to learn the relationship between features. Manual fusion of features can reduce the learning difficulty of the model and improve the effect.
# 将原施工日期和改造日期融合 features['YrBltAndRemod']=features['YearBuilt']+features['YearRemodAdd'] # 将地下室面积、1楼、2楼面积融合 features['TotalSF']=features['TotalBsmtSF'] + features['1stFlrSF'] + features['2ndFlrSF']
It can be found that the features we fuse are all features that are strongly related to SalePrice.
Finally simplify the features, and perform 01 processing on features with monotonous distribution (for example: 99 out of 100 data have a value of 0.9, and the other one has a value of 0.1).
features['haspool'] = features['PoolArea'].apply(lambda x: 1 if x > 0 else 0) features['has2ndfloor'] = features['2ndFlrSF'].apply(lambda x: 1 if x > 0 else 0)
2.6 生成最终训练数据
到这里特征工程就做完了, 我们需要从features中将训练集和测试集重新分离出来,构造最终的训练数据。
X = features.iloc[:len(y), :] X_sub = features.iloc[len(y):, :] X = np.array(X.copy()) y = np.array(y) X_sub = np.array(X_sub.copy())
三. 模型训练
因为SalePrice是数值型且是连续的,所以需要训练一个回归模型。
3.1 单一模型
首先以岭回归(Ridge) 为例,构造一个k折交叉验证模型。
from sklearn.linear_model import RidgeCV from sklearn.pipeline import make_pipeline from sklearn.model_selection import KFold kfolds = KFold(n_splits=10, shuffle=True, random_state=42) alphas_alt = [14.5, 14.6, 14.7, 14.8, 14.9, 15, 15.1, 15.2, 15.3, 15.4, 15.5] ridge = make_pipeline(RobustScaler(), RidgeCV(alphas=alphas_alt, cv=kfolds))
岭回归模型有一个超参数alpha,而RidgeCV的参数名是alphas,代表输入一个超参数alpha数组。在拟合模型时,会从alpha数组中选择表现较好某个取值。
由于现在只有一个模型,无法确定岭回归是不是最佳模型。所以我们可以找一些出场率高的模型多试试。
# lasso lasso = make_pipeline( RobustScaler(), LassoCV(max_iter=1e7, alphas=alphas2, random_state=42, cv=kfolds)) #elastic net elasticnet = make_pipeline( RobustScaler(), ElasticNetCV(max_iter=1e7, alphas=e_alphas, cv=kfolds, l1_ratio=e_l1ratio)) #svm svr = make_pipeline(RobustScaler(), SVR( C=20, epsilon=0.008, gamma=0.0003, )) #GradientBoosting(展开到一阶导数) gbr = GradientBoostingRegressor(...) #lightgbm lightgbm = LGBMRegressor(...) #xgboost(展开到二阶导数) xgboost = XGBRegressor(...)
有了多个模型,我们可以再定义一个得分函数,对模型评分。
#模型评分函数 def cv_rmse(model, X=X): rmse = np.sqrt(-cross_val_score(model, X, y, scoring="neg_mean_squared_error", cv=kfolds)) return (rmse)
以岭回归为例,计算模型得分。
score = cv_rmse(ridge)
print("Ridge score: {:.4f} ({:.4f})n".format(score.mean(), score.std()), datetime.now(), ) #0.1024
运行其他模型发现得分都差不多。
这时候我们可以任选一个模型,拟合,预测,提交训练结果。还是以岭回归为例
# 训练模型
ridge.fit(X, y)
# 模型预测
submission.iloc[:,1] = np.floor(np.expm1(ridge.predict(X_sub)))
# 输出测试结果
submission = pd.read_csv("./data/sample_submission.csv")
submission.to_csv("submission_single.csv", index=False)
submission_single.csv是岭回归预测的房价,我们可以把这个结果上传到 Kaggle 网站查看结果的得分和排名。
3.2 模型融合-stacking
有时候为了发挥多个模型的作用,我们会将多个模型融合,这种方式又被称为集成学习。
stacking 是一种常见的集成学习方法。简单来说,它会定义个元模型,其他模型的输出作为元模型的输入特征,元模型的输出将作为最终的预测结果。
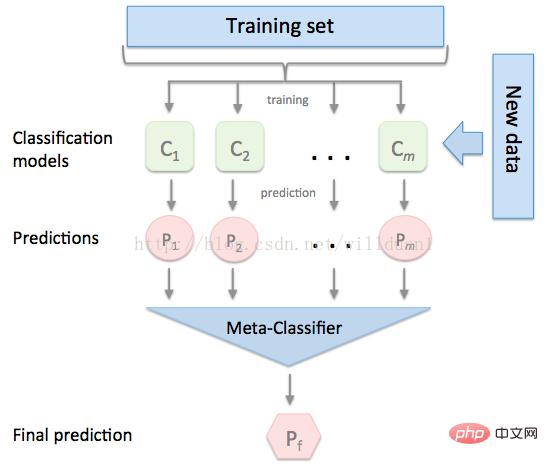
stacking
这里,我们用mlextend库中的StackingCVRegressor模块,对模型做stacking。
stack_gen = StackingCVRegressor( regressors=(ridge, lasso, elasticnet, gbr, xgboost, lightgbm), meta_regressor=xgboost, use_features_in_secondary=True)
训练、预测的过程与上面一样,这里不再赘述。
3.3 模型融合-线性融合
多模型线性融合的思想很简单,给每个模型分配一个权重(权重加和=1),最终的预测结果取各模型的加权平均值。
# 训练单个模型 ridge_model_full_data = ridge.fit(X, y) lasso_model_full_data = lasso.fit(X, y) elastic_model_full_data = elasticnet.fit(X, y) gbr_model_full_data = gbr.fit(X, y) xgb_model_full_data = xgboost.fit(X, y) lgb_model_full_data = lightgbm.fit(X, y) svr_model_full_data = svr.fit(X, y) models = [ ridge_model_full_data, lasso_model_full_data, elastic_model_full_data, gbr_model_full_data, xgb_model_full_data, lgb_model_full_data, svr_model_full_data, stack_gen_model ] # 分配模型权重 public_coefs = [0.1, 0.1, 0.1, 0.1, 0.15, 0.1, 0.1, 0.25] # 线性融合,取加权平均 def linear_blend_models_predict(data_x,models,coefs, bias): tmp=[model.predict(data_x) for model in models] tmp = [c*d for c,d in zip(coefs,tmp)] pres=np.array(tmp).swapaxes(0,1) pres=np.sum(pres,axis=1) return pres
到这里,房价预测的案例我们就讲解完了,大家可以自己运行一下,看看不同方式训练出来的模型效果。
回顾整个案例会发现,我们在数据预处理和特征工程上花费了很大心思,虽然机器学习问题模型原理比较难学,但实际过程中往往特征工程花费的心思最多。
The above is the detailed content of Use Python to make a house price prediction gadget!. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
 Choosing Between PHP and Python: A Guide
Apr 18, 2025 am 12:24 AM
Choosing Between PHP and Python: A Guide
Apr 18, 2025 am 12:24 AM
PHP is suitable for web development and rapid prototyping, and Python is suitable for data science and machine learning. 1.PHP is used for dynamic web development, with simple syntax and suitable for rapid development. 2. Python has concise syntax, is suitable for multiple fields, and has a strong library ecosystem.
 PHP and Python: Different Paradigms Explained
Apr 18, 2025 am 12:26 AM
PHP and Python: Different Paradigms Explained
Apr 18, 2025 am 12:26 AM
PHP is mainly procedural programming, but also supports object-oriented programming (OOP); Python supports a variety of paradigms, including OOP, functional and procedural programming. PHP is suitable for web development, and Python is suitable for a variety of applications such as data analysis and machine learning.
 How to solve the complexity of WordPress installation and update using Composer
Apr 17, 2025 pm 10:54 PM
How to solve the complexity of WordPress installation and update using Composer
Apr 17, 2025 pm 10:54 PM
When managing WordPress websites, you often encounter complex operations such as installation, update, and multi-site conversion. These operations are not only time-consuming, but also prone to errors, causing the website to be paralyzed. Combining the WP-CLI core command with Composer can greatly simplify these tasks, improve efficiency and reliability. This article will introduce how to use Composer to solve these problems and improve the convenience of WordPress management.
 PHP and Python: A Deep Dive into Their History
Apr 18, 2025 am 12:25 AM
PHP and Python: A Deep Dive into Their History
Apr 18, 2025 am 12:25 AM
PHP originated in 1994 and was developed by RasmusLerdorf. It was originally used to track website visitors and gradually evolved into a server-side scripting language and was widely used in web development. Python was developed by Guidovan Rossum in the late 1980s and was first released in 1991. It emphasizes code readability and simplicity, and is suitable for scientific computing, data analysis and other fields.
 Accelerate PHP code inspection: Experience and practice using overtrue/phplint library
Apr 17, 2025 pm 11:06 PM
Accelerate PHP code inspection: Experience and practice using overtrue/phplint library
Apr 17, 2025 pm 11:06 PM
During the development process, we often need to perform syntax checks on PHP code to ensure the correctness and maintainability of the code. However, when the project is large, the single-threaded syntax checking process can become very slow. Recently, I encountered this problem in my project. After trying multiple methods, I finally found the library overtrue/phplint, which greatly improves the speed of code inspection through parallel processing.
 How to optimize website performance: Experiences and lessons learned from using the Minify library
Apr 17, 2025 pm 11:18 PM
How to optimize website performance: Experiences and lessons learned from using the Minify library
Apr 17, 2025 pm 11:18 PM
In the process of developing a website, improving page loading has always been one of my top priorities. Once, I tried using the Miniify library to compress and merge CSS and JavaScript files in order to improve the performance of the website. However, I encountered many problems and challenges during use, which eventually made me realize that Miniify may no longer be the best choice. Below I will share my experience and how to install and use Minify through Composer.
 Solve CSS prefix problem using Composer: Practice of padaliyajay/php-autoprefixer library
Apr 17, 2025 pm 11:27 PM
Solve CSS prefix problem using Composer: Practice of padaliyajay/php-autoprefixer library
Apr 17, 2025 pm 11:27 PM
I'm having a tricky problem when developing a front-end project: I need to manually add a browser prefix to the CSS properties to ensure compatibility. This is not only time consuming, but also error-prone. After some exploration, I discovered the padaliyajay/php-autoprefixer library, which easily solved my troubles with Composer.
 Solve database connection problem: a practical case of using minii/db library
Apr 18, 2025 am 07:09 AM
Solve database connection problem: a practical case of using minii/db library
Apr 18, 2025 am 07:09 AM
I encountered a tricky problem when developing a small application: the need to quickly integrate a lightweight database operation library. After trying multiple libraries, I found that they either have too much functionality or are not very compatible. Eventually, I found minii/db, a simplified version based on Yii2 that solved my problem perfectly.




