Four cross-validation techniques you must learn in machine learning

​Introduction

Consider creating a model on a dataset, but it fails on unseen data.
We cannot simply fit a model to our training data and wait for it to run perfectly on real, unseen data.

This is an example of overfitting, where our model has extracted all the patterns and noise in the training data. To prevent this from happening, we need a way to ensure that our model has captured the majority of the patterns and is not picking up every bit of noise in the data (low bias and low variance). One of the many techniques for dealing with this problem is cross-validation.

Understanding cross-validation

Suppose in a specific data set, we have 1000 records, and we train_test_split() is executed on it. Assuming we have 70% training data and 30% test data random_state = 0, these parameters result in 85% accuracy. Now, if we set random_state = 50 let's say the accuracy improves to 87%.

This means that if we continue to choose precision values ​​for different random_state, fluctuations will occur. To prevent this, a technique called cross-validation comes into play.

Types of cross-validation

Leave one out cross-validation (LOOCV)

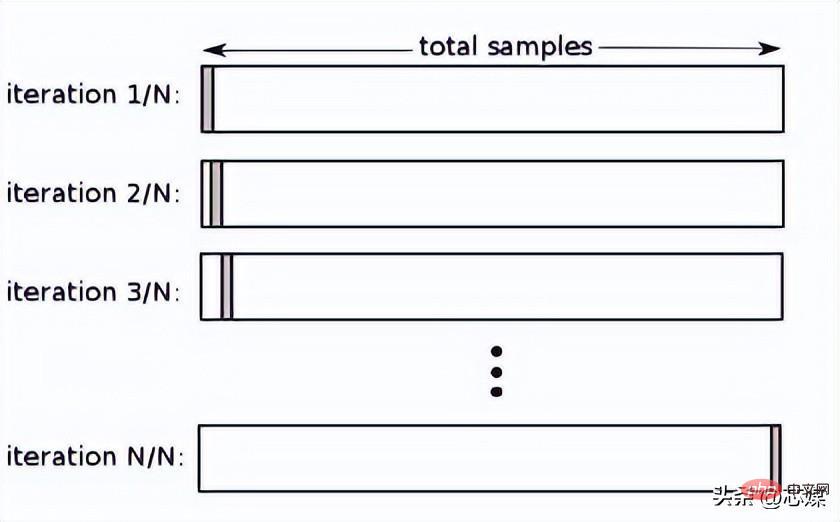
In LOOCV, we select 1 data point as testing, and all remaining data will be training data from the first iteration. In the next iteration, we will select the next data point as testing and the rest as training data. We will repeat this for the entire dataset so that the last data point is selected as the test in the final iteration.

Typically, to calculate the cross-validation R² for an iterative cross-validation procedure, you calculate the R² scores for each iteration and take their average.

Although it leads to reliable and unbiased estimates of model performance, it is computationally expensive to perform.

2. K-fold cross validation

in In K-fold CV, we split the data set into k subsets (called folds), then we train on all subsets, but leave one (k-1) subset for evaluation after training model.

Suppose we have 1000 records and our K=5. This K value means we have 5 iterations. The number of data points for the first iteration to be considered for the test data is 1000/5=200 from the start. Then for the next iteration, the next 200 data points will be considered tests, and so on.

To calculate the overall accuracy, we calculate the accuracy for each iteration and then take the average.

The minimum accuracy we can obtain from this process will be the lowest accuracy produced among all iterations, and likewise, the maximum accuracy will be among all iterations Produces the highest accuracy.

3.stratified cross-validation

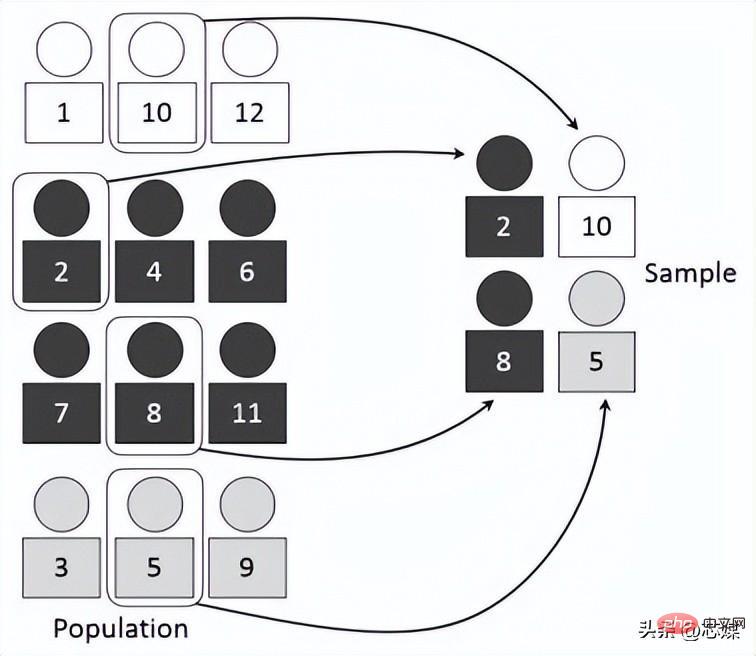
Hierarchical CV is an extension of regular k-fold cross-validation, but specifically for classification problems where the splits are not completely random and the ratio between target classes is the same at each fold as in the full dataset.

Suppose we have 1000 records, which contain 600 yes and 400 no. So, in each experiment, it ensures that the random samples populated into training and testing are populated in such a way that at least some instances of each class will be present in both the training and testing splits.

4.Time Series Cross Validation​

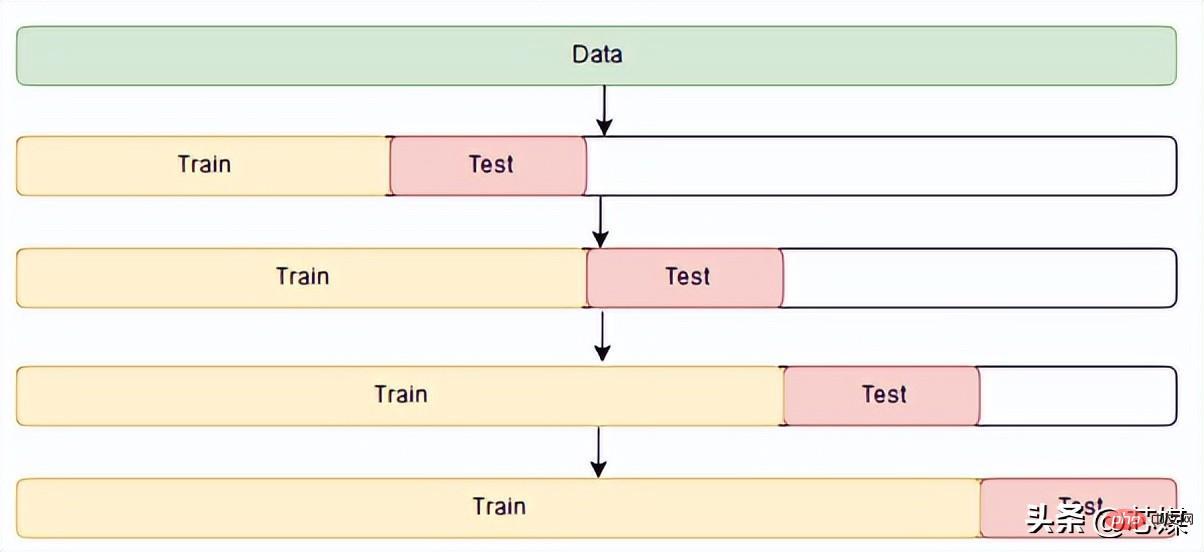
In time series CV there is a series of test sets, each test set contains an observation. The corresponding training set contains only observations that occurred before the observation that formed the test set. Therefore, future observations cannot be used to construct predictions.

Prediction accuracy is calculated by averaging the test set. This process is sometimes called the "evaluation of the rolling forecast origin" because the "origin" on which the forecast is based is rolled forward in time.

Conclusion

In machine learning, we usually don’t want the algorithm or model that performs best on the training set. Instead, we want a model that performs well on the test set, and a model that consistently performs well given new input data. Cross-validation is a critical step to ensure that we can identify such algorithms or models.

The above is the detailed content of Four cross-validation techniques you must learn in machine learning. For more information, please follow other related articles on the PHP Chinese website!