 Technology peripherals
Technology peripherals
 AI
AI
 Theoretical computer scientist Boaz Barak: Deep learning is not 'simple statistics”, and the distance between the two is getting farther and farther
Theoretical computer scientist Boaz Barak: Deep learning is not 'simple statistics”, and the distance between the two is getting farther and farther
Theoretical computer scientist Boaz Barak: Deep learning is not 'simple statistics”, and the distance between the two is getting farther and farther
In the 1990s, Rob Tibshirani, a well-known professor of bioinformatics at Stanford University, drew up a vocabulary to make a simple and rough correspondence between different concepts in machine learning and statistics:

#On the one hand, this table provides a basic understanding of machine learning, but at the same time, it simply summarizes the concepts in deep learning or machine learning It is the meaning of the word in statistics, and it also causes most people’s cognitive bias towards the nature of deep learning: that is, deep learning is “simple statistics”.
However, in in-depth discussion, this kind of cognition has hindered researchers to a certain extent from understanding the essential reasons for the success of deep learning. In an article "The uneasy relationship between deep learning and (classical) statistics" in June this year, Boaz Barak, a well-known Harvard professor and theoretical computer scientist, compared and distinguished deep learning and statistics, pointing out the fundamentals of deep learning. The constituent factors are very different from statistics.
Boaz Barak made an important observation: From the perspective of the purpose of the model, if it focuses on prediction and observation, then a deep learning model with black box characteristics may be the best choice; but If you want to gain a causal understanding of things and improve interpretability, then a "simple" model may perform better. This coincides with the "simplicity" view that constitutes one of the two principles of intelligence proposed by three scientists, Ma Yi, Cao Ying, and Shen Xiangyang, last month.
At the same time, Boaz Barak discussed its compatibility with deep learning by showing two different scenario cases of fitting statistical models and learning mathematics; he believed, While the math and code for deep learning are pretty much the same as fitting statistical models, at a deeper level a huge part of deep learning can be captured in the "teaching skills to students" scenario.
There is no doubt that statistical learning plays an important role in deep learning. But what is certain is that the statistical perspective cannot provide a complete picture for understanding deep learning. To understand different aspects of deep learning, people still need to approach it from different perspectives.
The following is Boaz Barak’s discussion:
1 Prediction and explanation in model fitting
For thousands of years, scientists have been fitting models to observations. For example, as mentioned in the book cover of Philosophy of Science, the Egyptian astronomer Ptolemy proposed an ingenious model of planetary motion. Ptolemy's model was geocentric (i.e., the planets revolved around the Earth), but had a series of "knobs" (specifically, epicycles) that gave it excellent predictive accuracy. In contrast, Copernicus' original heliocentric model assumed circular orbits of the planets around the sun. It is simpler (fewer "tunable knobs") and more correct overall than Ptolemy's model, but less accurate in predicting observations. (Copernicus later added his own epicycles, thus rivaling Ptolemy's performance.)
Ptolemy's and Copernicus's The model is unparalleled. When you need a "black box" to make predictions, the Ptolemaic geocentric model is superior. And if you want a simple model that can "peek inside" and serve as a theoretical starting point for explaining the motion of the stars, then Copernicus's model is better.In fact, Kepler eventually refined Copernicus's model into elliptical orbits and proposed his three laws of planetary motion, which allowed Newton to use the same ones that apply on Earth The laws of gravity explain them. To this end, it is crucial that the heliocentric model is not just a "black box" that provides predictions, but rather is given by simple mathematical equations with few "moving parts". Astronomy has been a source of inspiration for developing statistical techniques for many years. Gauss and Legendre (independently) invented least squares regression around 1800 for predicting the orbits of asteroids and other celestial bodies; Cauchy's invention of gradient descent in 1847 was also motivated by astronomical predictions.
In physics, (at least sometimes) you can "have it all" - find the "right" theory that leads to the best prediction accuracy and the best explanation of the data, which is explained by principles such as Occam's razor Such views capture the assumption that simplicity, predictive power, and explanatory insight are all mutually consistent. In many other fields, however, there is a tension between the twin goals of explanation (or, more generally, insight) and prediction. If you just want to predict the observation results, the "black box" may be the best choice. But if you're extracting causal models, general principles, or important features, then a simple model that's easy to understand and explain might be better.
The correct choice of model depends on its purpose. For example, consider a dataset that contains the gene expression and phenotypes of many individuals (say, for a certain disease). If the goal is to predict an individual's chance of getting sick, one will often want to use the best model for the task, no matter how complex or How many genes does it depend on. In contrast, if your goal is to identify a few genes for further study in a wet lab, a sophisticated black box will be of limited use, even if it is very accurate.
In 2001, Leo Breiman effectively explained this point in his famous article "Statistical Modeling: The Two Cultures" about statistical modeling. "Data modeling culture" focuses on simple generative models that explain the data, while "algorithm modeling culture" does not understand how the data is generated, but focuses on finding models that can predict the data. Breiman believes that statistics are too dominated by first cultures, and that this focus "leads to irrelevant theories and questionable scientific conclusions" and "prevents statisticians from studying exciting new questions."
However, Breiman’s paper was controversial. While Brad Efron agrees with some of the sentiments, “On first viewing, Leo Breiman’s exciting paper seems to reject simplicity and scientific insight in favor of a black box with a lot of knobs to manipulate. On second viewing, , it’s still the same.” But in a recent article ("Prediction, Estimation, and Attribution"), Efron generously admitted that "it turns out that Breiman was more prescient than me: Pure predictive algorithms have occupied the limelight of statistics in the 21st century, and their development The direction is pretty much the same as what Leo mentioned before. ”
2 Classic and Modern Prediction Models
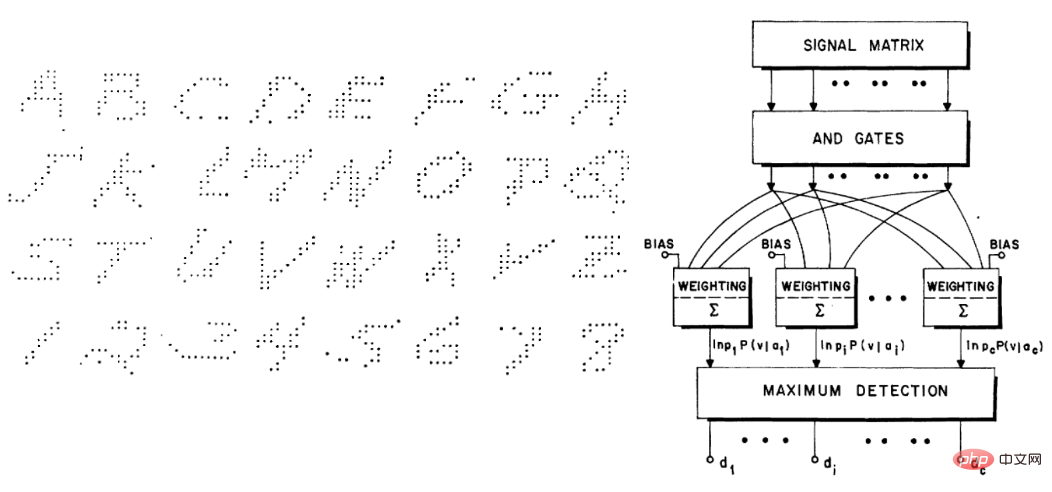
Whether machine learning is “deep” or not , it all belongs to what Breiman calls the second culture, that is, focuses on prediction, which has been circulating for a long time. For example, Duda and Hart's 1973 textbook "Deconstructing Distributions: A Pointwise Framework of Learning" and Highleyman's 1962 paper "The Design and Analysis of Pattern Recognition Experiments" are highly recognizable to today's deep learning practitioners. Very high:

Similarly, Highleyman’s handwritten character dataset and the architecture Chow used to fit the dataset (accuracy is approx. 58%) also resonates with modern readers.
3 Why is deep learning different?
In 1992, Stuart Geman, Elie Bienenstock and Rene Doursat co-wrote a paper titled "Neural Networks and the Bias/Varian Dilemma" which took some pessimistic views, for example, "Current feedforward neural networks are largely insufficient to solve difficult problems in machine perception and machine learning"; specifically, they believe that general-purpose neural networks cannot successfully solve difficult tasks, and the only way for neural networks to succeed is through Hand-designed features. In their words: "Important features must be built-in or 'hard-wired'... rather than learned through statistical methods.
”In hindsight, they were completely wrong. Moreover, modern neural network architectures such as Transformer are even more versatile than convolutional networks at the time. But it’s interesting to understand the reasons behind their mistakes.
I think the reason they made the mistake is that deep learning is indeed different from other learning methods. An a priori phenomenon is: deep learning seems to have just one more prediction model, like nearest neighbor or random forest. It may have more "knobs" but that seems to be a quantitative rather than qualitative difference. In the words of PW Andreson, “more is different”.
In physics, once the scale changes by several orders of magnitude, we often just need a completely different theory to explain it, and the same is true for deep learning. In fact, deep learning operates completely differently from classic models (parametric or non-parametric), even though from a high-level perspective, the equations (and Python code) look the same.
To explain this, let’s look at the learning process of two very different examples: Fitting a statistical model, and teaching students to learn mathematics.
Scenario A: Fitting a statistical model
Generally speaking, the steps for fitting a statistical model to data are as follows:
1. Let’s observe some data x and y. x can be regarded as a matrix of n ##, where 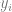 is the corresponding noise, additive noise is used for simplicity, and
is the corresponding noise, additive noise is used for simplicity, and 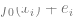 is the correct true label. )
is the correct true label. )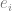 2. By running some optimization algorithm, we can fit the model
2. By running some optimization algorithm, we can fit the model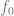 to the data so that
to the data so that
## The experience risk of # is minimal. That is, we use an optimization algorithm to find the minimized number of 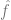
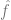 , where
, where 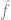 is a loss term (capturing
is a loss term (capturing 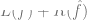 How close it is to y),
How close it is to y), 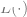 is an optional normalization term (trying to bias
is an optional normalization term (trying to bias 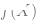 towards a simpler model).
towards a simpler model).
3. We hope that our model can have good overall loss because the generalization error/loss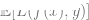 is small (this prediction is based on the overall data where the experimental data is to obtain).
is small (this prediction is based on the overall data where the experimental data is to obtain).
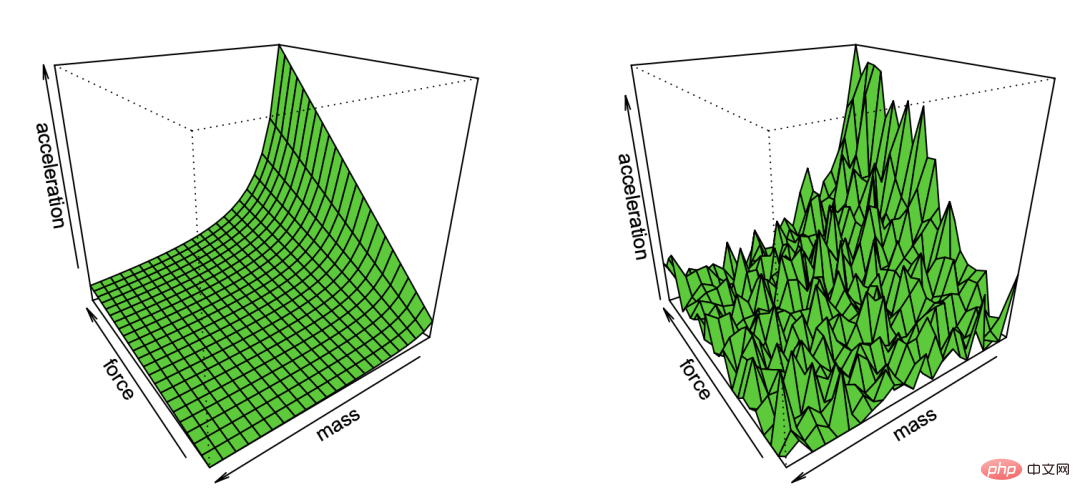
Caption: Newton’s first law cartoon reproduced by Bradley Efron through observation of noise
This very general paradigm encompasses many settings, including least squares linear regression, nearest neighbors, neural network training, and more. In a classic statistical setting, we would expect to observe the following:
Bias/variance trade-off: Consider F as the set of optimized models. (When we are in a non-convex setting and/or have a regularizer term, we can let F be the set of such models that can be implemented by the algorithm with non-negligible probability, given the effects of algorithm choice and regularizer.) The deviation of
F is the best approximation to the correct label, which can be achieved by the element 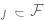 . The larger the class of F, the smaller the deviation. When
. The larger the class of F, the smaller the deviation. When 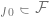 , the deviation can even be zero. However, when the F class is larger, more samples are needed to narrow its membership range, and thus the variance in the algorithm output model is larger. The overall generalization error is the sum of the bias term and the variance contribution.
, the deviation can even be zero. However, when the F class is larger, more samples are needed to narrow its membership range, and thus the variance in the algorithm output model is larger. The overall generalization error is the sum of the bias term and the variance contribution.
Thus, statistical learning often exhibits a bias/variance trade-off and minimizes the overall error through a "Goldilocks choice" of correct model complexity. In fact, Geman et al. do just that, justifying their pessimism about neural networks by saying that "the fundamental limitations resulting from the bias-variance dilemma apply to all non-parametric inference models, including neural networks."
More is not always best. In statistical learning, obtaining more features or data does not necessarily improve performance. For example, learning from data containing many irrelevant features is more challenging. Similarly, learning from a mixture model, where the data comes from one of two distributions (e.g.  and
and  ), is harder than learning the individual ones independently.
), is harder than learning the individual ones independently.
Diminishing returns. In many cases, the number of data points required to reduce prediction noise to some parameter  is in the order of
is in the order of  under some parameter k Form expansion. In this case, it takes about k samples to "take off", and once you do this, you will face a system of diminishing returns, that is, assuming that it takes n points to achieve (say) 90% accuracy, then you want To increase the accuracy to 95%, approximately another 3n points are needed. Generally speaking, as resources increase (whether data, model complexity, or computation), we want to capture more fine-grained distinctions rather than unlock new qualitative capabilities.
under some parameter k Form expansion. In this case, it takes about k samples to "take off", and once you do this, you will face a system of diminishing returns, that is, assuming that it takes n points to achieve (say) 90% accuracy, then you want To increase the accuracy to 95%, approximately another 3n points are needed. Generally speaking, as resources increase (whether data, model complexity, or computation), we want to capture more fine-grained distinctions rather than unlock new qualitative capabilities.
Strong dependence on loss and data. When fitting a model to high-dimensional data, a small detail may cause a big difference in the results. Statisticians know that choices like L1 or L2 regularizer are important, not to mention that using completely different data sets, different numbers of high-dimensional optimizers will be extremely different.
Data points have no natural "difficulty" (at least in some cases). Traditionally, data points are sampled independently of a distribution. Although points close to the decision boundary may be more difficult to classify, given the high-dimensional concentration of measurements, it is expected that most points will have similar distances. Therefore, at least in classical data distributions, points are not expected to differ greatly in their difficulty levels. However, mixed models can show different difficulty levels of this difference, so unlike the other problems mentioned above, this difference would not be very surprising in a statistical setting.
Scenario B: Learning Mathematics
In contrast to the above, let’s talk about teaching students some specific mathematical topics (such as calculating derivatives) and giving them general guidance and requirements. Do the exercises. This is not a formally defined setting, but some of its qualitative characteristics can be considered:
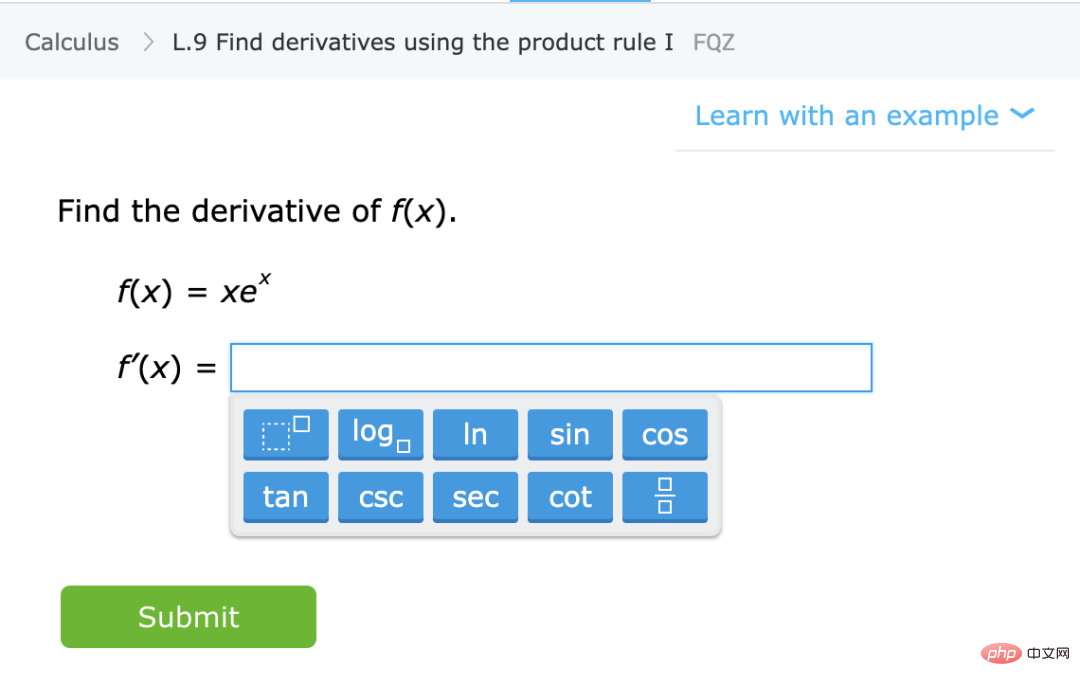
## Caption: Learn specific mathematics from the IXL website Practice of skills
#Learn a skill, not an approximate distribution. In this case, students are learning a skill rather than a certain quantity of estimators/predictors. While defining "skills" is not a trivial task, it is a qualitatively different goal. In particular, even if function mapping exercises cannot be used as a "black box" for solving some related tasks X, we believe that the internal representations students form when solving these problems are still useful for X.
The more, the better. Generally speaking, students will achieve better results if they practice more questions and different types of questions. But in fact, the "hybrid model"—doing some calculus problems and some algebra problems—doesn't affect students' performance in calculus and actually helps them learn.
"Explore" or unlock features, turn to automatic representation. While there are diminishing returns to problem solving at some point, students do seem to go through stages where doing problems helps concepts "click" and unlock new features. Additionally, when students repeat a particular type of problem, they appear to shift their ability and representation of those problems to a lower level, allowing them to develop some automaticity with those problems that they did not have before.
The performance part is independent of loss and data. There is more than one way to teach math concepts, and students may still end up learning the same material and similar internal representations, even if they use different books, educational methods, or grading systems.
Some questions are more difficult. In mathematics exercises, we can often see a strong correlation in the methods used by different students to solve the same problem. The difficulty of a problem seems to be fixed, and the order of solving the puzzles is also fixed, which allows the learning process to be optimized. This is actually what platforms such as IXL are doing.
4 Deep learning is more like statistical estimation or student learning skills?
So, which of the above two metaphors better describes modern deep learning, and specifically why it is so successful? Statistical model fitting seems more consistent with math and code. In fact, the standard Pytorch training loop trains deep networks through empirical risk minimization as described above:

However, at deeper levels Hierarchically, the relationship between the two settings is not so clear. Specifically, it can be carried out by repairing a specific learning task and using the "self-supervised learning linear probe (linear probe)" method to train the classification algorithm. The algorithm training is as follows:
1. Assume that the data is a sequence 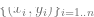 , where
, where 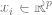 is a certain data point (such as a specific image),
is a certain data point (such as a specific image), 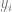 is a tag.
is a tag.
2. First find a deep neural network to represent the function 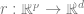 . The training of this function only uses data points
. The training of this function only uses data points 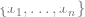 Instead of using labels, by minimizing some type of self-supervised loss function. Examples of such loss functions are reconstruction or picture-in-picture (recovering some part of another input x) or contrastive learning (finding
Instead of using labels, by minimizing some type of self-supervised loss function. Examples of such loss functions are reconstruction or picture-in-picture (recovering some part of another input x) or contrastive learning (finding 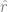 that makes
that makes 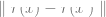 significant Smaller, when
significant Smaller, when 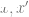 is the increment of the same data point, the parallel relationship is much smaller than the parallel relationship between two random points).
is the increment of the same data point, the parallel relationship is much smaller than the parallel relationship between two random points).
3. Then we use the complete labeled data 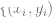 to fit a linear classifier
to fit a linear classifier 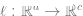 (where C is the class number) to minimize the cross-entropy loss. The final classifier resulted in a mapping of
(where C is the class number) to minimize the cross-entropy loss. The final classifier resulted in a mapping of 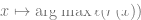 . Step 3 is only suitable for linear classifiers, so the "magic" happens in step 2 (self-supervised learning of deep networks). In self-supervised learning, some properties that can be seen include:
. Step 3 is only suitable for linear classifiers, so the "magic" happens in step 2 (self-supervised learning of deep networks). In self-supervised learning, some properties that can be seen include:
Learn a skill rather than approximating a function. Self-supervised learning is not about approximating a function, but learning representations that can be used for a variety of downstream tasks. Assuming that this is the dominant paradigm in natural language processing, whether downstream tasks are obtained by linear probing, fine-tuning, or prompting is secondary.
The more, the better. In self-supervised learning, the quality of representation improves as the amount of data increases. And, the more diverse the data, the better.
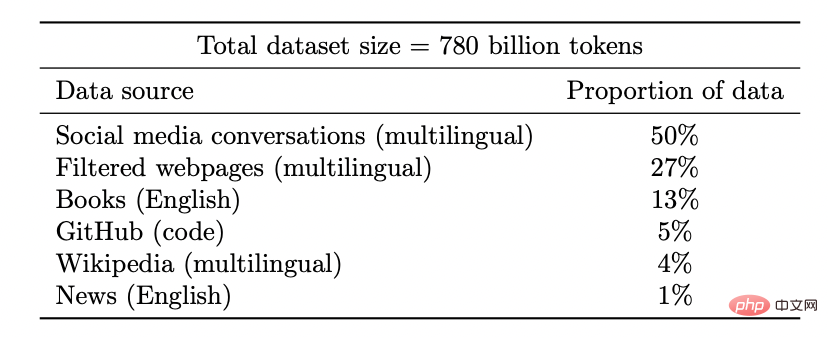
Legend: Data set of Google PaLM model
Unlock abilities. As resources (data, computation, model size) expand, discontinuous improvements in deep learning models are seen time and time again, and this is also demonstrated in some synthetic environments.
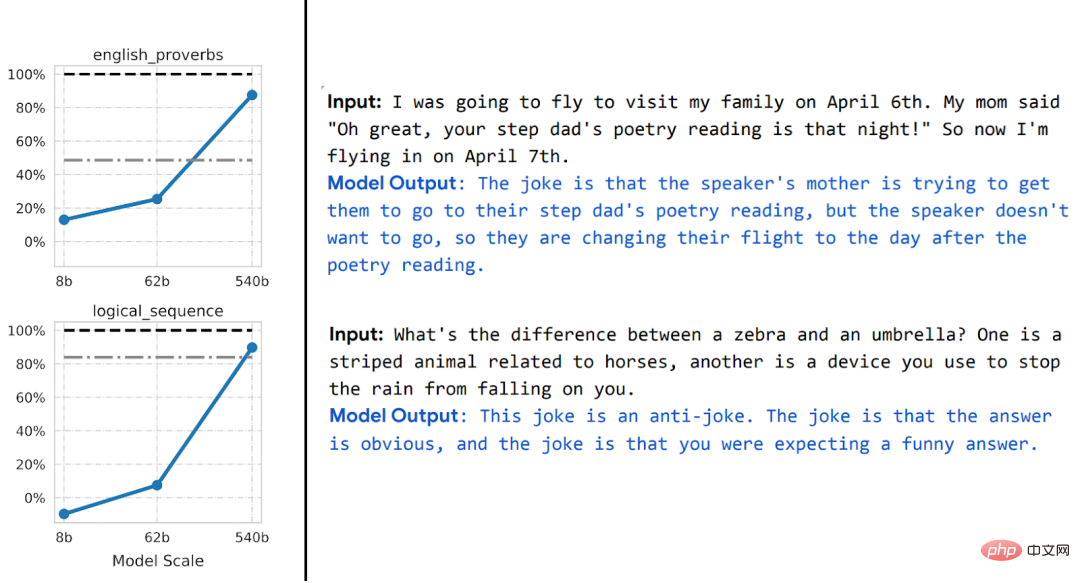
Note: As the model size increases, the PaLM model shows some discrete improvements in some benchmarks (there are only three size caveats in the above figure) and unlocks some commands. Functions that surprise people, such as explaining jokes.
#Performance is largely independent of loss or data. More than one self-supervised loss, several contrastive and reconstructive losses are used for images. Language models sometimes use one-sided reconstruction (predicting the next token), and sometimes they use masking models, where the goal is to predict masked input from the left and right tokens.
It is also possible to use a slightly different data set, which may affect efficiency, but as long as "reasonable" choices are made, in general, the original resource is better than the specific one used Loss or dataset is more predictive of performance.
#Some instances are harder than others. This is not limited to self-supervised learning, data points may have some inherent "difficulty levels".
In fact, there are several practical evidences that different learning algorithms have different "skill levels" and different points have different "difficulty levels" (The probability that classifier f correctly classifies x increases one-way with the skill of f and decreases one-way with the difficulty of x). The "skill and difficulty" paradigm is the clearest explanation of the "online accuracy" phenomenon discovered by Recht and Miller et al., and in the paper I co-authored with Kaplun, Ghosh, Garg, and Nakkiran, I also show that in the data set How different inputs have an inherent "difficulty signature" that conventionally appears to be robust to different models.
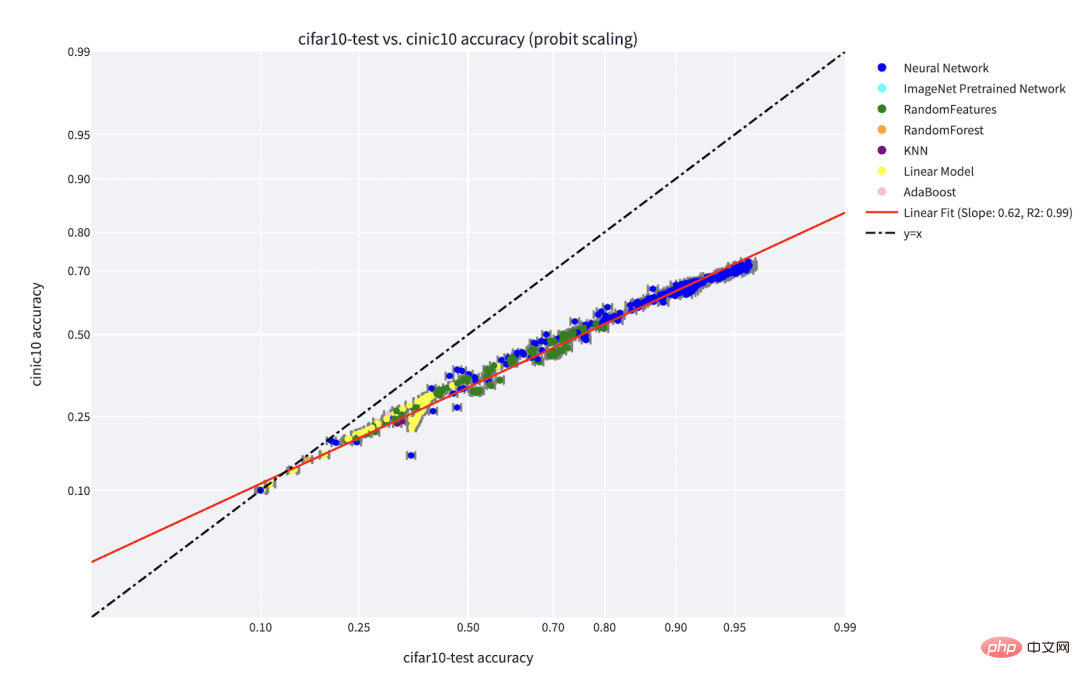
Chart: Miller et al.’s graph shows a classifier trained on CIFAR-10 and tested on CINIC-10 Line phenomenon accuracy
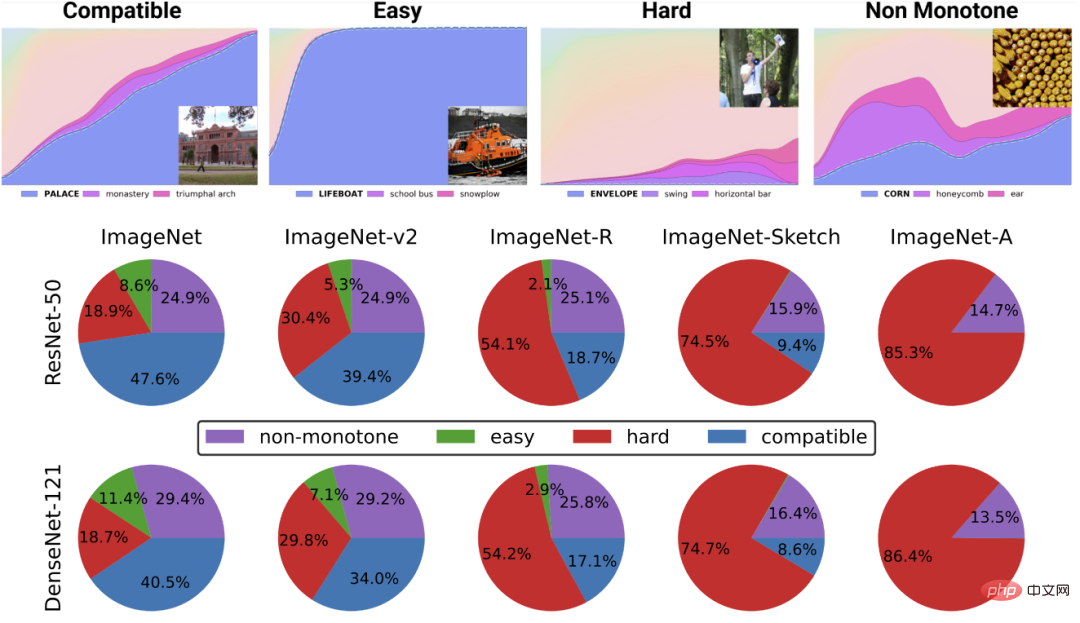
# Distributions: A Pointwise Framework of Learning" to obtain an increasing number of resource classifiers. The top chart depicts different softmax probabilities for the most likely class as a function of the global accuracy of a classifier indexed by training time; the bottom pie chart shows the breakdown of different datasets into different types of points. Notably, this decomposition is similar for different neural architectures.
Training is teaching. 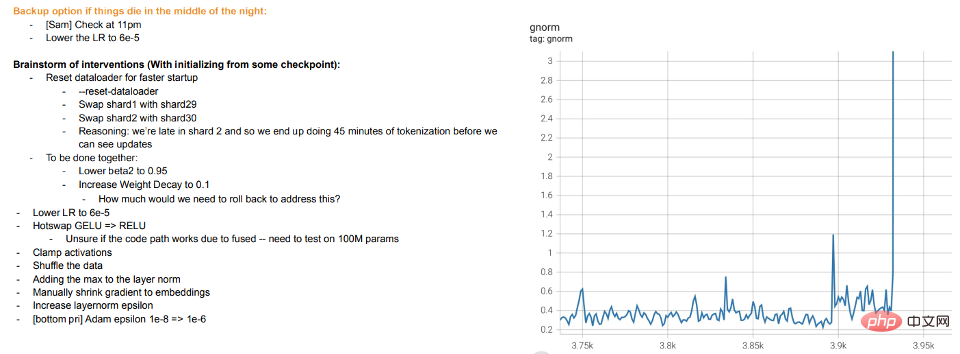
 Modern training of large models seems more like teaching students rather than adapting the model to the data,
Modern training of large models seems more like teaching students rather than adapting the model to the data,
Illustration: Excerpt from Meta’s training log
Two situations are discussed below:
###Scenario 1: Supervised Learning#########So far, we have only discussed self-supervised learning, but the typical example of deep learning is still supervised learning. After all, deep learning "ImageNet Moments" is from ImageNet. So, does what we discussed above apply to supervised learning? ######First of all, The emergence of supervised large-scale deep learning is to some extent a historical accident, thanks to the availability of large, high-quality labeled data sets (i.e., ImageNet). It is possible to imagine an alternative history: deep learning first made breakthroughs in natural language processing through unsupervised learning, and then moved to vision and supervised learning.
Second, there is some evidence that Even though supervised learning and self-supervised learning use completely different loss functions, they behave similarly "behind the scenes". Both usually achieve the same performance. It was also found in the paper "Revisiting Model Stitching to Compare Neural Representations" that they learned similar internal representations. Specifically, for each 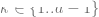 , one can "stitch" the first k layers of a deep d model trained with self-supervision with the last d-k layers of the supervised model and make the performance almost Maintain the original level.
, one can "stitch" the first k layers of a deep d model trained with self-supervision with the last d-k layers of the supervised model and make the performance almost Maintain the original level.
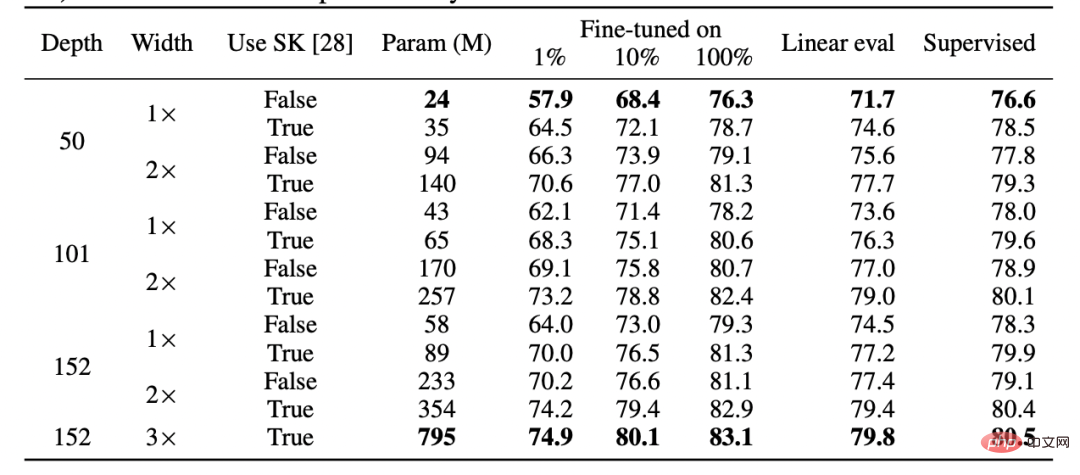
Caption: Table from Hinton’s team’s paper “Big Self-Supervised Models are Strong Semi-Supervised Learners”. Note the general similarity in performance of supervised learning, fine-tuning (100%) self-supervised and self-supervised linear detection
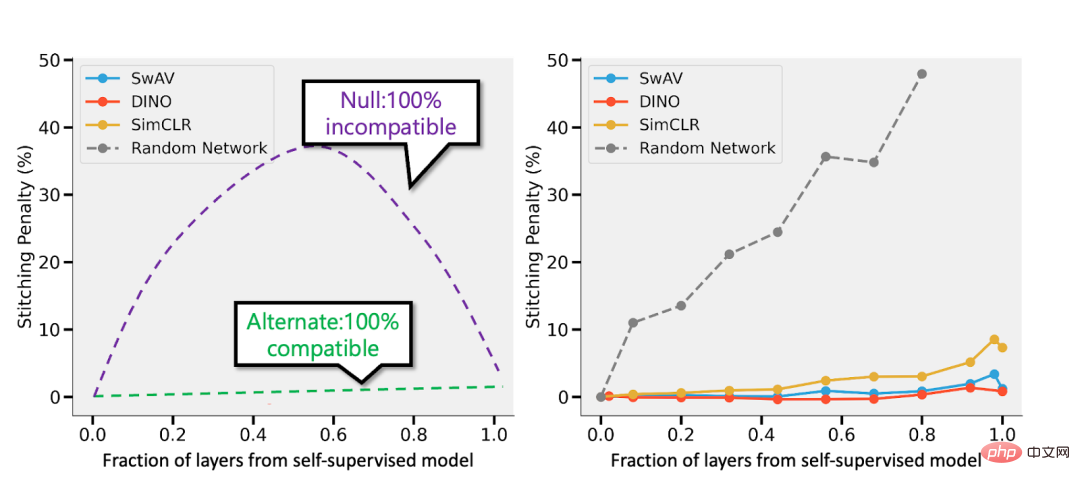
Note: Excerpted from the self-supervision and supervision model of the paper "Revisiting Model Stitching to Compare Neural Representations". Left - If the self-supervised model is 3% less accurate than the supervised model, then a fully compatible representation will incur a splicing penalty of p 3% (when p layers are from the self-supervised model). If the models are completely incompatible, expect accuracy to drop dramatically as more models are stitched together. Right - Actual results of splicing different self-supervised models.
The advantage of self-supervised simple models is that they can combine feature learning or "deep learning magic" (the result of a deep representation function) with statistical model fitting ( Done by a linear or other "simple" classifier, separated out on top of this representation) .
Finally, although speculative, it seems that “meta-learning” is often equated with the fact that learning representations (see the paper “Rapid Learning or Feature Reuse? Towards Understanding the Effectiveness” for details of MAML"), can be seen as another piece of evidence supporting the point of this article, regardless of what the model is ostensibly optimized for.
Case 2: Over-parameterization
Readers may have noticed that I skipped typical examples of differences between statistical learning models and deep learning models in practical applications. , that is, the lack of "bias-variance trade-off" and the excellent generalization ability of over-parameterized models.
There are two reasons why I won’t talk about these examples in detail:
First, if supervised learning is indeed equivalent to self-supervised simple “bottom layer” Learning, then its generalization ability can be explained (for details, please see the paper "For self-supervised learning, Rationality implies generalization, provably");
Secondly, I think Over-parameterization is not the key to success in deep learning. What makes deep networks special is not that they are large compared to the number of samples, but that they are large in absolute terms. In fact, there is usually no over-parameterization in unsupervised/self-supervised learning models. Even for large-scale language models, they just have larger data sets, but that doesn't make their performance any less mysterious.
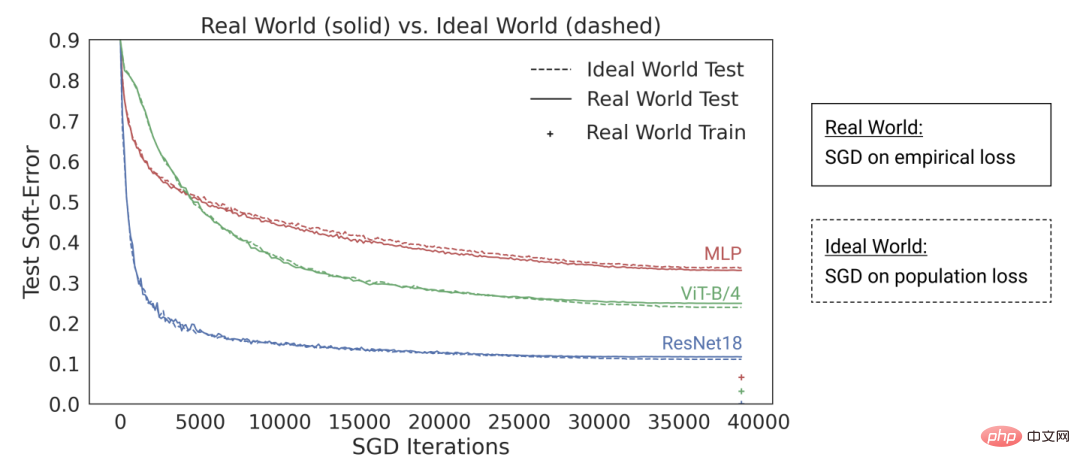
Illustration: In the paper "The Deep Bootstrap Framework: Good Online Learners are Good Offline Generalizers", the researchers' findings show that today's deep learning architecture suffers from "over-parameterization" and The performance is similar in the "undersampled" state (where the model is trained on limited data for many generations until it overfits: the "real world" shown above), in the "underparameterized" and "online" cases This is also true (where the model is only trained for one generation, and each sample is only seen once: that is, the "ideal world" in the picture above)
5 Summary
There is no doubt that statistical learning plays an important role in deep learning. However, if you think of deep learning simply as a model that fits more knobs than a classical model, you miss many of the factors behind its success. The so-called "human student" metaphor is even more inappropriate.
Deep learning is similar to biological evolution in that although there are many repeated applications of the same rule (i.e., gradient descent with experience loss), it produces highly complex results. Different components of a neural network appear to learn different things at different times, including representation learning, predictive fitting, implicit regularization, and pure noise. We are still looking for the right lens to ask questions about deep learning, let alone answer them.
There is a long way to go and we will work together to encourage you.
The above is the detailed content of Theoretical computer scientist Boaz Barak: Deep learning is not 'simple statistics”, and the distance between the two is getting farther and farther. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Methods and steps for using BERT for sentiment analysis in Python
Jan 22, 2024 pm 04:24 PM
Methods and steps for using BERT for sentiment analysis in Python
Jan 22, 2024 pm 04:24 PM
BERT is a pre-trained deep learning language model proposed by Google in 2018. The full name is BidirectionalEncoderRepresentationsfromTransformers, which is based on the Transformer architecture and has the characteristics of bidirectional encoding. Compared with traditional one-way coding models, BERT can consider contextual information at the same time when processing text, so it performs well in natural language processing tasks. Its bidirectionality enables BERT to better understand the semantic relationships in sentences, thereby improving the expressive ability of the model. Through pre-training and fine-tuning methods, BERT can be used for various natural language processing tasks, such as sentiment analysis, naming
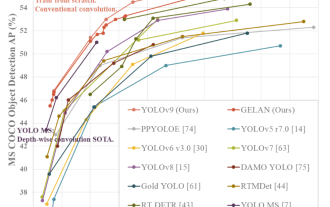 YOLO is immortal! YOLOv9 is released: performance and speed SOTA~
Feb 26, 2024 am 11:31 AM
YOLO is immortal! YOLOv9 is released: performance and speed SOTA~
Feb 26, 2024 am 11:31 AM
Today's deep learning methods focus on designing the most suitable objective function so that the model's prediction results are closest to the actual situation. At the same time, a suitable architecture must be designed to obtain sufficient information for prediction. Existing methods ignore the fact that when the input data undergoes layer-by-layer feature extraction and spatial transformation, a large amount of information will be lost. This article will delve into important issues when transmitting data through deep networks, namely information bottlenecks and reversible functions. Based on this, the concept of programmable gradient information (PGI) is proposed to cope with the various changes required by deep networks to achieve multi-objectives. PGI can provide complete input information for the target task to calculate the objective function, thereby obtaining reliable gradient information to update network weights. In addition, a new lightweight network framework is designed
 Latent space embedding: explanation and demonstration
Jan 22, 2024 pm 05:30 PM
Latent space embedding: explanation and demonstration
Jan 22, 2024 pm 05:30 PM
Latent Space Embedding (LatentSpaceEmbedding) is the process of mapping high-dimensional data to low-dimensional space. In the field of machine learning and deep learning, latent space embedding is usually a neural network model that maps high-dimensional input data into a set of low-dimensional vector representations. This set of vectors is often called "latent vectors" or "latent encodings". The purpose of latent space embedding is to capture important features in the data and represent them into a more concise and understandable form. Through latent space embedding, we can perform operations such as visualizing, classifying, and clustering data in low-dimensional space to better understand and utilize the data. Latent space embedding has wide applications in many fields, such as image generation, feature extraction, dimensionality reduction, etc. Latent space embedding is the main
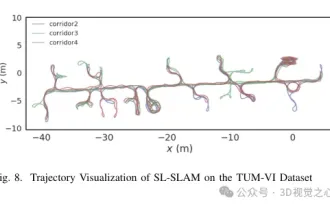 Beyond ORB-SLAM3! SL-SLAM: Low light, severe jitter and weak texture scenes are all handled
May 30, 2024 am 09:35 AM
Beyond ORB-SLAM3! SL-SLAM: Low light, severe jitter and weak texture scenes are all handled
May 30, 2024 am 09:35 AM
Written previously, today we discuss how deep learning technology can improve the performance of vision-based SLAM (simultaneous localization and mapping) in complex environments. By combining deep feature extraction and depth matching methods, here we introduce a versatile hybrid visual SLAM system designed to improve adaptation in challenging scenarios such as low-light conditions, dynamic lighting, weakly textured areas, and severe jitter. sex. Our system supports multiple modes, including extended monocular, stereo, monocular-inertial, and stereo-inertial configurations. In addition, it also analyzes how to combine visual SLAM with deep learning methods to inspire other research. Through extensive experiments on public datasets and self-sampled data, we demonstrate the superiority of SL-SLAM in terms of positioning accuracy and tracking robustness.
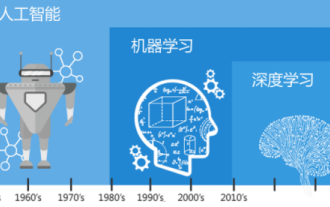 Understand in one article: the connections and differences between AI, machine learning and deep learning
Mar 02, 2024 am 11:19 AM
Understand in one article: the connections and differences between AI, machine learning and deep learning
Mar 02, 2024 am 11:19 AM
In today's wave of rapid technological changes, Artificial Intelligence (AI), Machine Learning (ML) and Deep Learning (DL) are like bright stars, leading the new wave of information technology. These three words frequently appear in various cutting-edge discussions and practical applications, but for many explorers who are new to this field, their specific meanings and their internal connections may still be shrouded in mystery. So let's take a look at this picture first. It can be seen that there is a close correlation and progressive relationship between deep learning, machine learning and artificial intelligence. Deep learning is a specific field of machine learning, and machine learning
 Super strong! Top 10 deep learning algorithms!
Mar 15, 2024 pm 03:46 PM
Super strong! Top 10 deep learning algorithms!
Mar 15, 2024 pm 03:46 PM
Almost 20 years have passed since the concept of deep learning was proposed in 2006. Deep learning, as a revolution in the field of artificial intelligence, has spawned many influential algorithms. So, what do you think are the top 10 algorithms for deep learning? The following are the top algorithms for deep learning in my opinion. They all occupy an important position in terms of innovation, application value and influence. 1. Deep neural network (DNN) background: Deep neural network (DNN), also called multi-layer perceptron, is the most common deep learning algorithm. When it was first invented, it was questioned due to the computing power bottleneck. Until recent years, computing power, The breakthrough came with the explosion of data. DNN is a neural network model that contains multiple hidden layers. In this model, each layer passes input to the next layer and
 1.3ms takes 1.3ms! Tsinghua's latest open source mobile neural network architecture RepViT
Mar 11, 2024 pm 12:07 PM
1.3ms takes 1.3ms! Tsinghua's latest open source mobile neural network architecture RepViT
Mar 11, 2024 pm 12:07 PM
Paper address: https://arxiv.org/abs/2307.09283 Code address: https://github.com/THU-MIG/RepViTRepViT performs well in the mobile ViT architecture and shows significant advantages. Next, we explore the contributions of this study. It is mentioned in the article that lightweight ViTs generally perform better than lightweight CNNs on visual tasks, mainly due to their multi-head self-attention module (MSHA) that allows the model to learn global representations. However, the architectural differences between lightweight ViTs and lightweight CNNs have not been fully studied. In this study, the authors integrated lightweight ViTs into the effective
 AlphaFold 3 is launched, comprehensively predicting the interactions and structures of proteins and all living molecules, with far greater accuracy than ever before
Jul 16, 2024 am 12:08 AM
AlphaFold 3 is launched, comprehensively predicting the interactions and structures of proteins and all living molecules, with far greater accuracy than ever before
Jul 16, 2024 am 12:08 AM
Editor | Radish Skin Since the release of the powerful AlphaFold2 in 2021, scientists have been using protein structure prediction models to map various protein structures within cells, discover drugs, and draw a "cosmic map" of every known protein interaction. . Just now, Google DeepMind released the AlphaFold3 model, which can perform joint structure predictions for complexes including proteins, nucleic acids, small molecules, ions and modified residues. The accuracy of AlphaFold3 has been significantly improved compared to many dedicated tools in the past (protein-ligand interaction, protein-nucleic acid interaction, antibody-antigen prediction). This shows that within a single unified deep learning framework, it is possible to achieve





