Two years after Ian Goodfellow and other researchers introduced generative adversarial networks in a paper, Yann LeCun called adversarial training "the most interesting idea in ML in the past decade." Although GANs are interesting and promising, they are only part of a family of generative models that solve traditional AI problems from a completely different perspective. In this article we will compare three common generative models.
When we think of machine learning, the first thing that probably comes to mind is the discriminant algorithm. Discriminative models are the prediction of labels or categories of input data based on its characteristics and are at the heart of all classification and prediction solutions. In contrast to these models, generative algorithms help us tell stories about the data and provide possible explanations of how the data was generated. Unlike discriminative algorithms, which map features to labels, generative models try to predict features given a label.
Distinguish the relationship between the label y and the feature x defined by the model, and generate the model to answer the question "How do you get y". The generative model model is P(Observation/Cause), and then uses Bayes' theorem to calculate P(Cause/Observation). In this way, they can capture p(x|y), the probability of x given y, or the probability of a feature given a label or class. So in fact, generative algorithms can also be used as classifiers, probably because they model the distribution of individual classes.
There are many generative algorithms, but the most popular models that fall into the category of deep generative models are variational autoencoders (VAEs), gans, and flow-based models.
A variational autoencoder (VAE) is a generative model that "provides a probabilistic description of observations in a latent space." Simply put, this means that VAE stores latent attributes as probability distributions.
The idea of variational autoencoders (Kingma & Welling, 2014) or VAEs is deeply rooted in variational Bayesian and graphical model methods.
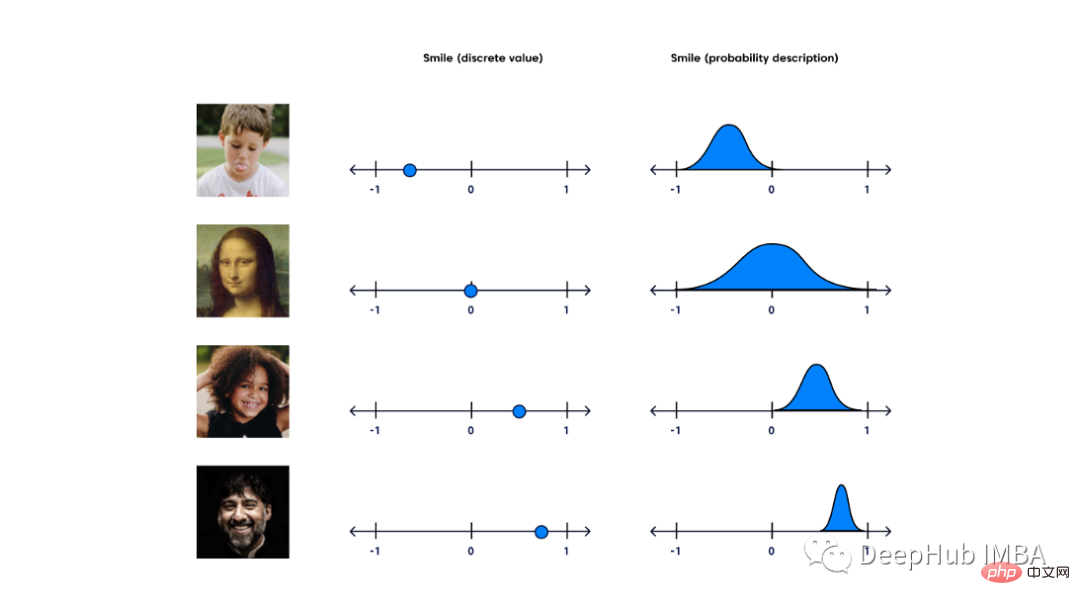
The standard autoencoder consists of 2 similar networks, an encoder and a decoder. The encoder takes the input and converts it into a smaller representation, which the decoder can use to convert it back to the original input. The latent space into which they transform the input and the space in which their encoding vectors lie may not be continuous. This is a problem for generative models, as we all want to sample randomly from a latent space, or generate variations of the input image from a continuous latent space.
The variational autoencoder has a continuous latent space, which makes random sampling and interpolation more convenient. To achieve this, the hidden nodes of the encoder do not output the encoding vector, but instead output two vectors of the same size: a mean vector and a standard deviation vector. Each hidden node considers itself Gaussian distributed. The i-th element of the mean and standard deviation vector here corresponds to the mean and standard deviation value of the i-th random variable. We sample from this distribution vector and the decoder randomly samples from the probability distribution of the input vector. This process is random generation. This means that even for the same input, when the mean and standard deviation are held constant, the actual encoding will differ in each pass.
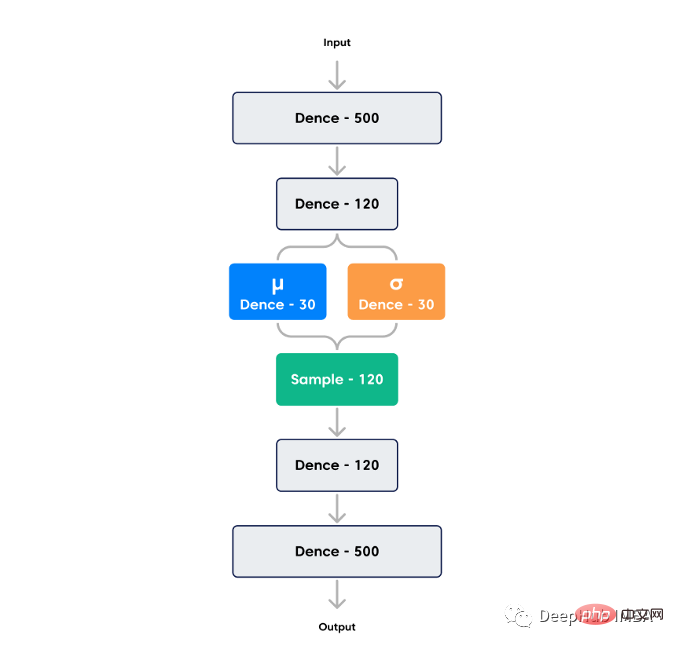
The loss of the autoencoder is to minimize the reconstruction loss (how similar the output is to the input) and the latent loss (how close the hidden nodes are to the normal distribution). The smaller the potential loss, the less information can be encoded, so the reconstruction loss will increase, so there is a trade-off between the potential loss and the reconstruction loss. When the potential loss is small, the generated image will be too similar to the training image, resulting in poor performance. When the reconstruction loss is small, the reconstructed image effect during training is better, but the generated new image is quite different from the reconstructed image, so a good balance needs to be found.
VAEs can handle various types of data, sequential and non-sequential, continuous or discrete, even labeled or unlabeled, which makes them very powerful generation tools.
But a major drawback of VAEs is the blurry output they generate. As Dosovitskiy and Brox pointed out, VAE models often produce unrealistic and ambiguous samples. This is caused by the way the data distribution is recovered and the loss function is calculated. A 2017 paper by Zhao et al. suggested modifying VAEs without using variational Bayesian methods to improve output quality.
Generative adversarial networks (GANs) are a generative model based on deep learning that can generate new content. The GAN architecture was first described in a 2014 paper titled "Generative Adversarial Networks" by Ian Goodfellow et al.
GANs employ a supervised learning approach using two sub-models: a generator model that generates new examples and a discriminator model that attempts to classify examples as real or fake (generated).
Generator: A model used to generate new plausible examples from the problem domain.
Frequency Discriminator: A model used to classify examples as real (from the domain) or fake (generated).
The two models are trained as competitors. Generators produce sample data directly. Its opponent, the discriminator, attempts to distinguish between samples drawn from the training data and samples drawn from the generator. This competitive process continues during training until the discriminator model fails to tell true or false more than half the time, which means that the generator model is generating very realistic data.
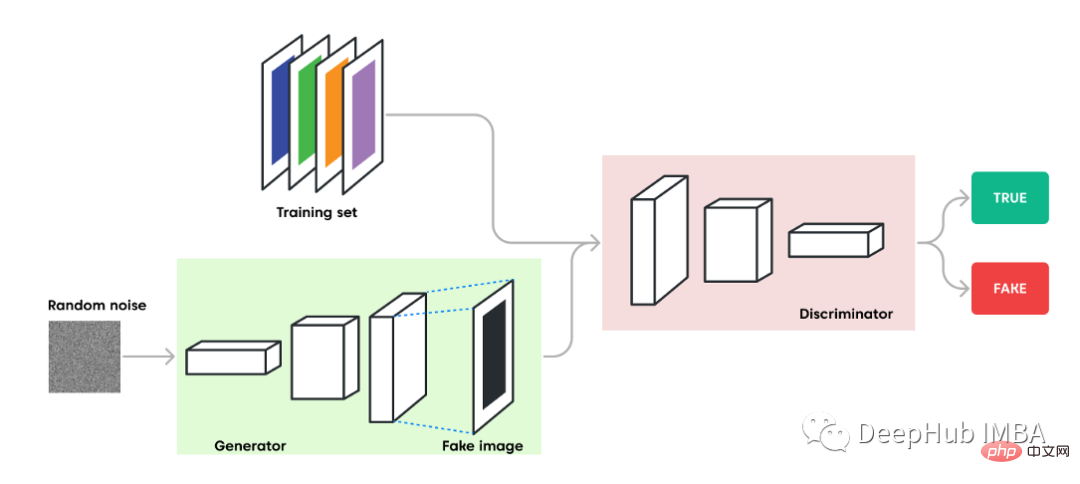
#When the discriminator successfully identifies a real or fake sample, it is rewarded while its parameters remain unchanged. If the generator makes a mistake, it is punished and its parameters are updated. In an ideal world, whenever the discriminator can't tell the difference and predicts "uncertain" (e.g., 50% true or false), the generator can produce a perfect copy from the input domain.
But here each model can overpower the other. If the discriminator is too good, it will return values very close to 0 or 1, and the generator will have trouble getting updated gradients. If the generator is too good, it will exploit the discriminator's weaknesses and cause false negatives. Therefore, the two neural networks must have similar "skill levels" achieved through their respective learning rates. This is also one of the reasons why GAN is difficult to train.
The generator takes a fixed-length random vector as input and generates a sample within the defined domain. This vector is randomly drawn from a Gaussian distribution. After training, the points in this multi-dimensional vector space will correspond to the points in the problem domain, forming a compressed representation of the data distribution. This step is similar to VAE. This vector space is called a latent space, or a vector space composed of latent variables. . The GAN's generator will average selected points in the latent space. New points extracted from the latent space can be provided as input to the generator model and used to generate new and different output examples. After training, the generator model is retained and used to generate new samples.
The discriminator model takes an example as input (either a real sample from the training dataset or generated by a generator model) and predicts a binary class label of real or fake( has been generated). The discriminator is a normal (and easy to understand) classification model.
After the training process, the discriminator is discarded because we are interested in the generator. Of course the discriminator can also be used for other purposes.
GANs can produce feasible samples, but the original GAN also has shortcomings:
Flow-based generative models are exact log-likelihood models with tractable sampling and latent variable inference. Flow-based models apply a bunch of reversible transformations to samples from the prior so that the exact log-likelihood of an observation can be calculated. Unlike the previous two algorithms, this model explicitly learns the data distribution, so the loss function is negative log-likelihood.
In nonlinear independent component analysis, the flow model f is constructed as an invertible mapping of high-dimensional random variables x to standard Gaussian latent variables z=f(x) Transform. The key idea in the design of the flow model is that it can be an arbitrary bijective function and can be formed by superposing simple reversible transformations. To summarize: the flow model f is composed of a series of reversible flows as f(x) =f1◦···◦fL(x), with each fi having a tractable inverse and a tractable Jacobian matrix. Mode.
There are two broad categories of flow-based models: models with normalized flow and models with autoregressive flow that attempt to enhance the performance of the base model.
Being able to perform good density estimation is essential for many machine learning problems. But it is inherently complex: when we need to perform backpropagation in a deep learning model, the embedded probability distribution needs to be simple enough so that the derivatives can be calculated efficiently. The traditional solution is to use Gaussian distributions in latent variable generation models, although most real-world distributions are much more complex. Normalized flow (NF) models, such as RealNVP or Glow, provide a robust approximation of the distribution. They transform a simple distribution into a complex distribution by applying a series of reversible transformation functions. Through a series of transformations, according to the variable transformation theorem, the original variables can be repeatedly replaced with new variables, and finally the probability distribution of the final target variable is obtained.
When the flow transformation in the normalized flow is framed as an autoregressive model, where each dimension in the vector variable is conditioned on the previous dimension, the flow model This change in is called autoregressive flow. It is a step forward compared to models with standardized processes.
Commonly used autoregressive flow models are PixelCNN for image generation and WaveNet for one-dimensional audio signals. They all consist of a bunch of causal convolutions - convolution operations that take order into account: predictions at a specific timestamp only use data observed in the past. In PixelCNN, causal convolution is performed by a masked kernel. And WaveNet shifts the output through several timestamps into the future time.
Flow-based models are conceptually very friendly to modeling complex distributions, but they suffer from density estimation performance issues compared to state-of-the-art autoregressive models limits. Although flow models may initially produce good output as an alternative to GANs, there is a significant gap in training computational cost between them, with flow-based models taking several times longer to generate images of the same resolution than GANs.
Each algorithm has its advantages and limitations in terms of accuracy and efficiency. Although GANs and process-based models generally generate better or closer to real images than VAE, the latter has faster time and better parameter efficiency than process-based models. Here is a comparison summary of the three models:
You can see that GAN is very efficient because of its parallelism, but it is not reversible. In contrast, flow models are reversible but not efficient, while vae is reversible and efficient but cannot be computed in parallel. Based on these characteristics, we can make trade-offs between output, training process, and efficiency in actual use.
The above is the detailed content of Detailed comparison of generative models VAE, GAN and flow-based models. For more information, please follow other related articles on the PHP Chinese website!
![[Web front-end] Node.js quick start](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
