A neural network-based strategy to enhance quantum simulations

Recent quantum computers provide a promising platform for finding the ground state of quantum systems, a fundamental task in physics, chemistry and materials science. However, recent methods are limited by noise and limited recent quantum hardware resources.

Researchers at the University of Waterloo in Canada have introduced neural error mitigation, which uses neural networks to improve estimates of ground-state and ground-state observables obtained using recent quantum simulations. To demonstrate the method's broad applicability, the researchers employed neural error mitigation to find H2 prepared by a variational quantum eigensolver. and LiH molecular Hamiltonian and the ground state of the lattice Schwinger model.

Experimental results show that neural error mitigation improves numerical and experimental variational quantum feature solver calculations to produce low energy errors, high fidelity, and robustness to more complex solvable Accurate estimation of observed quantities such as order parameters and entanglement entropy without requiring additional quantum resources. Furthermore, neural error mitigation is independent of the quantum state preparation algorithm used, the quantum hardware implementing it, and the specific noise channels affecting the experiment, contributing to its versatility as a quantum simulation tool.

The research is titled "Neural Error Mitigation of Near-Term Quantum Simulations" and was published in "Nature Machine" on July 20, 2022 Intelligence》.

Since the early 20th century, scientists have been developing comprehensive theories that describe the behavior of quantum mechanical systems. However, the computational costs required to study these systems often exceed the capabilities of current scientific computing methods and hardware. Therefore, computational infeasibility remains an obstacle to the practical application of these theories to scientific and technical problems.

Simulation of quantum systems on quantum computers (referred to here as quantum simulation) shows promise in overcoming these obstacles and has been a fundamental driving force behind the concept and creation of quantum computers. In particular, quantum simulations of the ground and steady states of quantum many-body systems beyond the capabilities of classical computers are expected to have a significant impact on nuclear physics, particle physics, quantum gravity, condensed matter physics, quantum chemistry, and materials science. The capabilities of current and near-term quantum computers continue to be limited by limitations such as the number of qubits and the effects of noise. Quantum error correction technology can eliminate errors caused by noise, providing a way for fault-tolerant quantum computing. In practice, however, implementing quantum error correction incurs significant overhead in terms of the number of qubits required and low error rates, both of which are beyond the capabilities of current and near-term devices.

Until fault-tolerant quantum simulations can be achieved, modern variational algorithms significantly alleviate the need for quantum hardware and take advantage of the capabilities of noisy, moderate-scale quantum devices.

A prominent example is the variational quantum eigensolver (VQE), a hybrid quantum classical algorithm that iterates through a series of variational optimization of parameterized quantum circuits Ground approach to the lowest energy eigenvalue of the target Hamiltonian. Among other variational algorithms, this has become a leading strategy for achieving quantum advantage using recent devices and accelerating progress in multiple fields of science and technology.

Experimental implementation of variational quantum algorithms remains a challenge for many scientific problems because noisy mid-scale quantum devices are affected by various noise sources and defects. Currently, several quantum error mitigation (QEM) methods for mitigating these issues have been proposed and experimentally verified, thereby improving quantum computing without the quantum resources required for quantum error correction.

Typically, these methods use specific information about the noise channels affecting quantum computation, hardware implementation, or the quantum algorithm itself; including implicit representations of noise models and how they affect the desired Estimation of observed quantities, specific knowledge of the state subspace in which prepared quantum states should reside, and characterization and mitigation of noise sources on various components of quantum computing, such as single-qubit and two-qubit gate errors, as well as state preparation and measurement error.

Machine learning techniques have recently been repurposed as tools to solve complex problems in quantum many-body physics and quantum information processing, providing an alternative approach to QEM. Here, researchers from the University of Waterloo introduce a QEM strategy called neural error mitigation (NEM), which uses neural networks to mitigate errors in the approximate preparation of the quantum ground state of the Hamiltonian.

The NEM algorithm consists of two steps. First, the researchers performed neural quantum state (NQS) tomography (NQST) to train NQS ansatz to represent approximate ground states prepared by noisy quantum devices using experimentally accessible measurements. Inspired by traditional quantum state tomography (QST), NQST is a data-driven QST machine learning method that uses a limited number of measurements to efficiently reconstruct complex quantum states.

The variational Monte Carlo (VMC) algorithm is then applied on the same NQS ansatz (also known as NEM ansatz) to improve the representation of the unknown ground state. In the spirit of VQE, VMC approximates the ground state of the Hamiltonian based on the classical variational ansatz, in the example NQS ansatz.

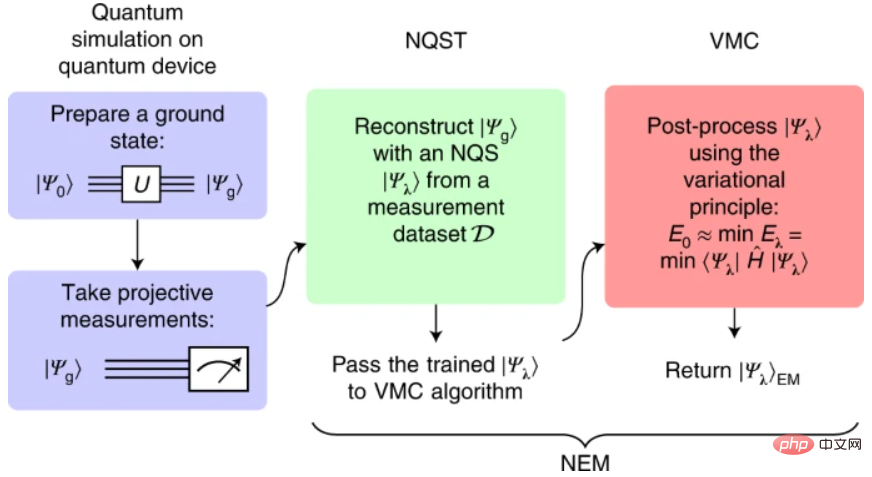
Illustration: NEM program. (Source: Paper)

Here, the researchers used an autoregressive generative neural network as NEM ansatz; more specifically, they used the Transformer architecture and showed that the model Performing well as an NQS. Due to its ability to simulate long-range temporal and spatial correlations, this architecture has been used in many state-of-the-art experiments in the fields of natural language and image processing, and has the potential to simulate long-range quantum correlations.

NEM has several advantages over other error mitigation techniques. First, it has low experimental overhead; it requires only a simple set of experimentally feasible measurements to learn the properties of noisy quantum states prepared by VQE. Therefore, the overhead of error mitigation in NEM is shifted from quantum resources (i.e., performing additional quantum experiments and measurements) to classical computing resources for machine learning. In particular, the researchers noted that the main cost of NEM is performing VMC before convergence. Another advantage of NEM is that it is independent of the quantum simulation algorithm, the device that implements it, and the specific noise channels that affect the quantum simulation. Therefore, it can also be combined with other QEM techniques and can be applied to simulate quantum analog or digital quantum circuits.

Illustration: Experimental and numerical NEM results of the molecular Hamiltonian. (Source: Paper)

NEM also solves the problem of low measurement accuracy that arises when estimating quantum observables using recent quantum devices. This is particularly important in quantum simulations, where accurate estimation of quantum observables is crucial for practical applications. NEM essentially solves the problem of low measurement accuracy at each step of the algorithm. In a first step, NQST improves the variance of the observable estimates at the cost of introducing a small estimate bias. This bias, as well as the residual variance, can be further reduced by training NEM ansatz with VMC, which leads to zero-variance expectations of energy estimates after reaching the ground state.

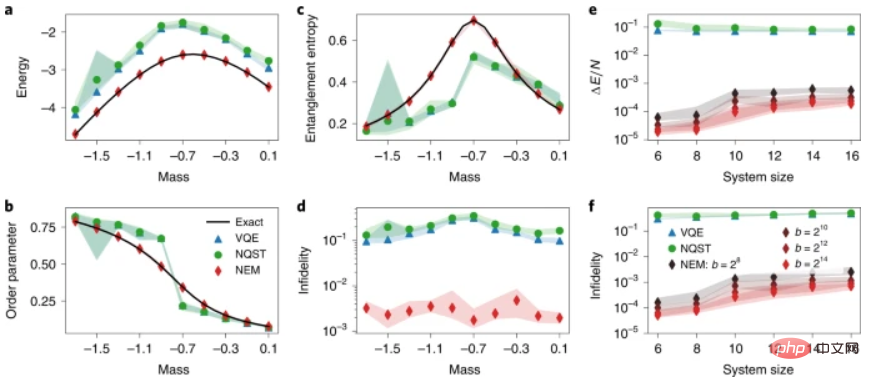Illustration: The properties of the NEM applied to the ground state of the lattice Schwinger model. (Source: paper)

By combining the use of parametric quantum circuits as the VQE of ansatz, and the use of neural networks as the NQST and VMC of ansatz, NEM combines two parametric quantum state families and three optimization problems regarding its losses. The researchers raised questions about the nature of the relationships between these families of states, their losses and quantum advantages. Examining these relationships provides a new way to study the potential of noisy, medium-scale quantum algorithms in the pursuit of quantum advantage. This may facilitate a better demarcation between simulations of classically tractable quantum systems and simulations that require quantum resources.

Paper link: ​https://www.nature.com/articles/s42256-022-00509-0​

Related reports: ​https://techxplore.com/news/2022-08-neural-networkbased-strategy-near-term-quantum.html​

The above is the detailed content of A neural network-based strategy to enhance quantum simulations. For more information, please follow other related articles on the PHP Chinese website!