The accuracy of GPT-3 in solving math problems has increased to 92.5%! Microsoft proposes MathPrompter to create 'science' language models without fine-tuning

The most criticized shortcoming of large language models, apart from serious nonsense, is probably their "inability to do math".

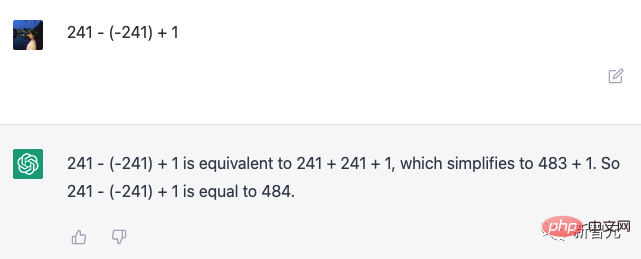
For example, for a complex mathematical problem that requires multi-step reasoning, the language model usually cannot give the correct answer, even if there is With the blessing of "thinking chain" technology, errors often occur in the intermediate steps.

Different from natural language understanding tasks in the liberal arts, mathematics problems usually have only one correct answer, and the range of answers is not so open, making the task of generating accurate solutions difficult for large language models. Say it's more challenging.

Moreover, when it comes to mathematical problems, existing language models usually do not provide confidence for their answers, leaving users unable to judge the credibility of the generated answers.

In order to solve this problem, Microsoft Research proposed MathPrompter technology, which can improve the performance of LLM on arithmetic problems while increasing its reliance on prediction.

Paper link: https://arxiv.org/abs/2303.05398

MathPrompter uses Zero-shot thinking Chain hinting technology generates multiple algebraic expressions or Python functions to solve the same mathematical problem in different ways, thereby increasing the confidence of the output results.

Compared with other hint-based CoT methods, MathPrompter also checks the validity of intermediate steps.

Based on 175B parameter GPT, using MathPrompter method to increase the accuracy of MultiArith data set from 78.7% to 92.5%!

Prompt specializing in mathematics

In recent years, the development of natural language processing is largely due to the continuous expansion in scale of large language models (LLMs) , which demonstrated amazing zero-shot and few-shot capabilities, and also contributed to the development of prompting technology. Users only need to enter a few simple examples into LLM in prompt to predict new tasks.

prompt can be said to be quite successful for single-step tasks, but in tasks requiring multi-step reasoning, the performance of prompt technology is still insufficient.

When humans solve a complex problem, they will break it down and try to solve it step by step. The "Chain of Thought" (CoT) prompting technology extends this intuition to LLMs , performance improvements have been achieved across a range of NLP tasks requiring inference.

This paper mainly studies the Zero-shot-CoT method "for solving mathematical reasoning tasks". Previous work has achieved significant accuracy improvements on the MultiArith data set. It has improved from 17.7% to 78.7%, but there are still two key shortcomings:

#1. Although the thinking chain followed by the model improves the results, it does not check the thinking chain. Prompt the effectiveness of each step followed;

2. No confidence is provided for the LLM prediction results.

MathPrompter

To address these gaps to some extent, researchers took inspiration from "the way humans solve math problems" and broke down complex problems into simpler multi-step procedure, and utilizes multiple methods to validate the method at each step.

#Since LLM is a generative model, it becomes very tricky to ensure that the generated answers are accurate, especially for mathematical reasoning tasks.

Researchers observed the process of students solving arithmetic problems and summarized several steps students took to verify their solutions:

Compliance with known results By comparing the solution with known results, you can evaluate its accuracy and make necessary adjustments; when the problem is a This is especially useful when it comes to standard problems with mature solutions.

Multi-verification, by approaching the problem from multiple angles and comparing the results, helps confirm the effectiveness of the solution and ensures that it is both reasonable and precise.

Cross-checking, the process of solving the problem is as necessary as the final answer; verifying the correctness of the intermediate steps in the process can provide a clear understanding of the solution The thought process behind it.

Compute verification, using a calculator or computer to perform arithmetic calculations can help verify the accuracy of the final answer

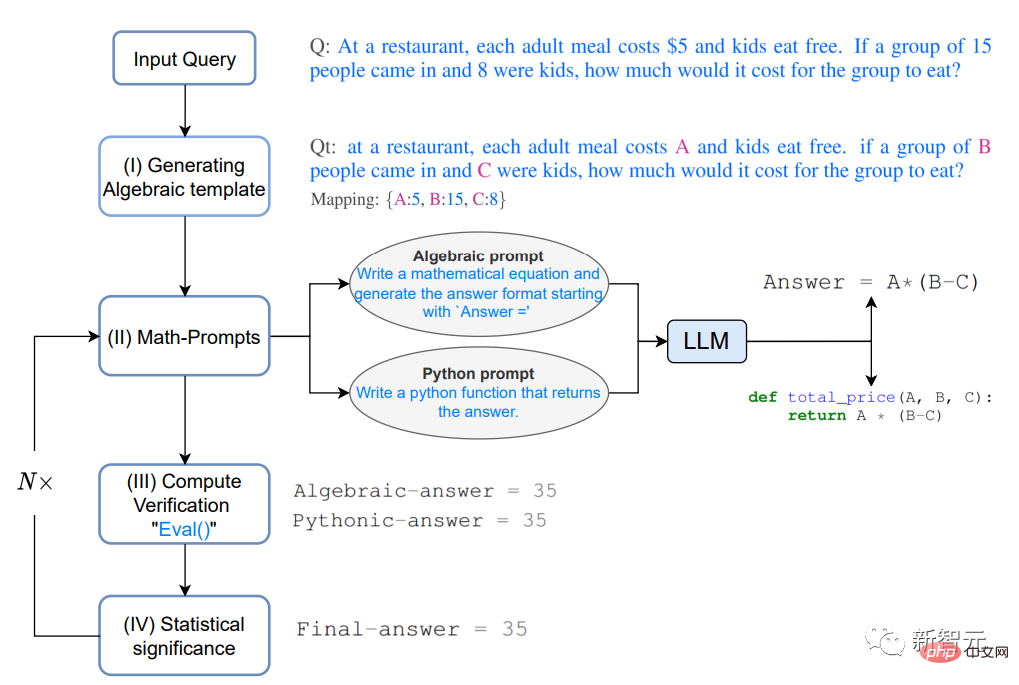
Specifically, given a question Q,

## In a restaurant, the cost of each adult meal The price is $5, and children eat free. If 15 people come in and 8 of them are children, how much does it cost to eat for this group of people?

1. Generating Algebraic template

##First solve the problem Translated to algebraic form, by replacing the numeric terms with variables using a key-value map, we get the modified question Qt

# #2. Math-promptsBased on the intuition provided by the above thought process of multiple verification and cross-checking, two different methods are used to generate Qt The analytical solution, both algebraically and Pythonic, gives LLM the following hints to generate additional context for Qt.

The prompt can be "Derive an algebraic expression" or "Write a Python function"

LLM model can output the following expression after responding to the prompt.

The analysis plan generated above provides users with tips about the "intermediate thinking process" of LLM. Adding additional tips can improve the accuracy of the results. accuracy and consistency, which in turn improves MathPrompter's ability to generate more precise and efficient solutions.

3. Compute verificationUse multiple input variables in Qt A random key-value map to evaluate the expressions generated in the previous step, using Python's eval() method to evaluate these expressions.

Then compare the output results to see if you can find a consensus in the answer, which can also provide a higher degree of confidence that the answer is correct and reliable.

Once the expression agrees on the output, the variable values ​​in the input Q are used to calculate the final answer.

4. Statistical significance

To ensure consensus in the output of various expressions, Repeat steps 2 and 3 approximately 5 times in the experiment and report the most frequently observed answer value.

In the absence of clear consensus, repeat steps 2, 3, and 4.

Experimental results

MathPrompter was evaluated on the MultiArith data set. The mathematical questions in it were specifically used to test the machine learning model's ability to perform complex arithmetic operations and reasoning. Requires application of various arithmetic operations and logical reasoning to solve successfully.

The accuracy results on the MultiArith data set show that MathPrompter performs better than all Zero-shot and Zero -shot-CoT baseline, increasing the accuracy from 78.7% to 92.5%

It can be seen that the performance of the MathPrompter model based on 175B parameter GPT3 DaVinci is comparable to that of the 540B parameter model and SOTA's Few -shot-CoT method equivalent.

As you can see from the above table, the design of MathPrompter can make up for problems such as "The generated answers sometimes have one step difference. ” problem can be avoided by running the model multiple times and reporting consensus results.

In addition, the problem that the inference step may be too lengthy can be solved by Pythonic or Algebraic methods, which usually require fewer tokens

In addition, the inference steps may be correct, but the final calculation result is incorrect. MathPrompter solves this problem by using Python's eval() method function.

In most cases, MathPrompter can generate correct intermediate and final answers, but there are a few cases, such as the last question in the table, where the algebraic and Pythonic outputs are consistent. Yes, but there is an error.

The above is the detailed content of The accuracy of GPT-3 in solving math problems has increased to 92.5%! Microsoft proposes MathPrompter to create 'science' language models without fine-tuning. For more information, please follow other related articles on the PHP Chinese website!