 Technology peripherals
Technology peripherals
 AI
AI
 Are modular machine learning systems enough? Bengio teachers and students tell you the answer
Are modular machine learning systems enough? Bengio teachers and students tell you the answer
Are modular machine learning systems enough? Bengio teachers and students tell you the answer
Deep learning researchers draw inspiration from neuroscience and cognitive science. From hidden units and input methods to the design of network connections and network architecture, many breakthrough studies are based on imitating brain operation strategies. There is no doubt that modularity and attention have been frequently used in combination in artificial networks in recent years and achieved impressive results.
In fact, cognitive neuroscience research shows that the cerebral cortex represents knowledge in a modular way, with communication between different modules, and the attention mechanism for content selection, which is what is mentioned above. The mentioned modularity and attention combinations are used. In recent research, it has been suggested that this mode of communication in the brain may have implications for inductive bias in deep networks. The sparsity of dependencies between these high-level variables breaks down knowledge into recombinable fragments that are as independent as possible, making learning more efficient.
Although much recent research relies on such modular architectures, researchers have used a large number of techniques and architectural modifications that make it possible to analyze real, usable systems. Architectural principles become challenging.
Machine learning systems are gradually revealing the advantages of sparser and more modular architectures. Modular architectures not only have good generalization performance, but also bring better distribution out-of-distribution. (OoD) Generalization, scalability, learning speed, and interpretability. A key to the success of such systems is that data-generating systems used in real-world settings are considered to consist of sparsely interacting parts, and it would be helpful to give the model a similar inductive bias. However, since these real-world data distributions are complex and unknown, the field has been lacking rigorous quantitative evaluations of these systems.
A paper written by three researchers from the University of Montreal in Canada: Sarthak Mittal, Yoshua Bengio, and Guillaume Lajoie. They used simple and known modular data distribution to analyze common modules. A comprehensive assessment of the architecture was conducted. The study highlights the benefits of modularity and sparsity and reveals insights into the challenges faced when optimizing modular systems. The first author and corresponding author, Sarthak Mittal, is a master student of Bengio and Lajoie.

- Paper address: https://arxiv.org/pdf/2206.02713.pdf
- GitHub Address: https://github.com/sarthmit/Mod_Arch
Specifically, this study extends the analysis of Rosenbaum et al. and proposes a Methods to evaluate, quantify, and analyze common components of modular architecture. To this end, the research developed a series of benchmarks and metrics designed to explore the effectiveness of modular networks. This reveals valuable insights that help identify not only where current approaches succeed, but also when and how these approaches fail.
The contribution of this study can be summarized as:
- This study develops benchmark tasks and metrics based on probabilistic selection rules, and uses benchmarks and metrics to quantify modularity Two important phenomena in systems: collapse and specialization.
- This study extracts commonly used modular inductive biases and systematically evaluates them through a series of models designed to extract commonly used architectural properties (Monolithic, Modular, Modular-op, GT-Modular models ).
- The study found that specialization in a modular system can significantly improve model performance when there are many potential rules in a task, but not when there are only few.
- The study found that standard modular systems tend to be suboptimal in both their ability to focus on the right information and their ability to specialize, suggesting the need for additional inductive bias.
Definition / Terminology
In this paper, researchers explore how a series of modular systems perform common tasks that Formulated by a synthetic data generation process we call rule data. They introduce the definition of key components, including (1) rules and how these rules form tasks, (2) modules and how these modules adopt different model architectures, (3) specialization and how models are evaluated. The detailed settings are shown in Figure 1 below.
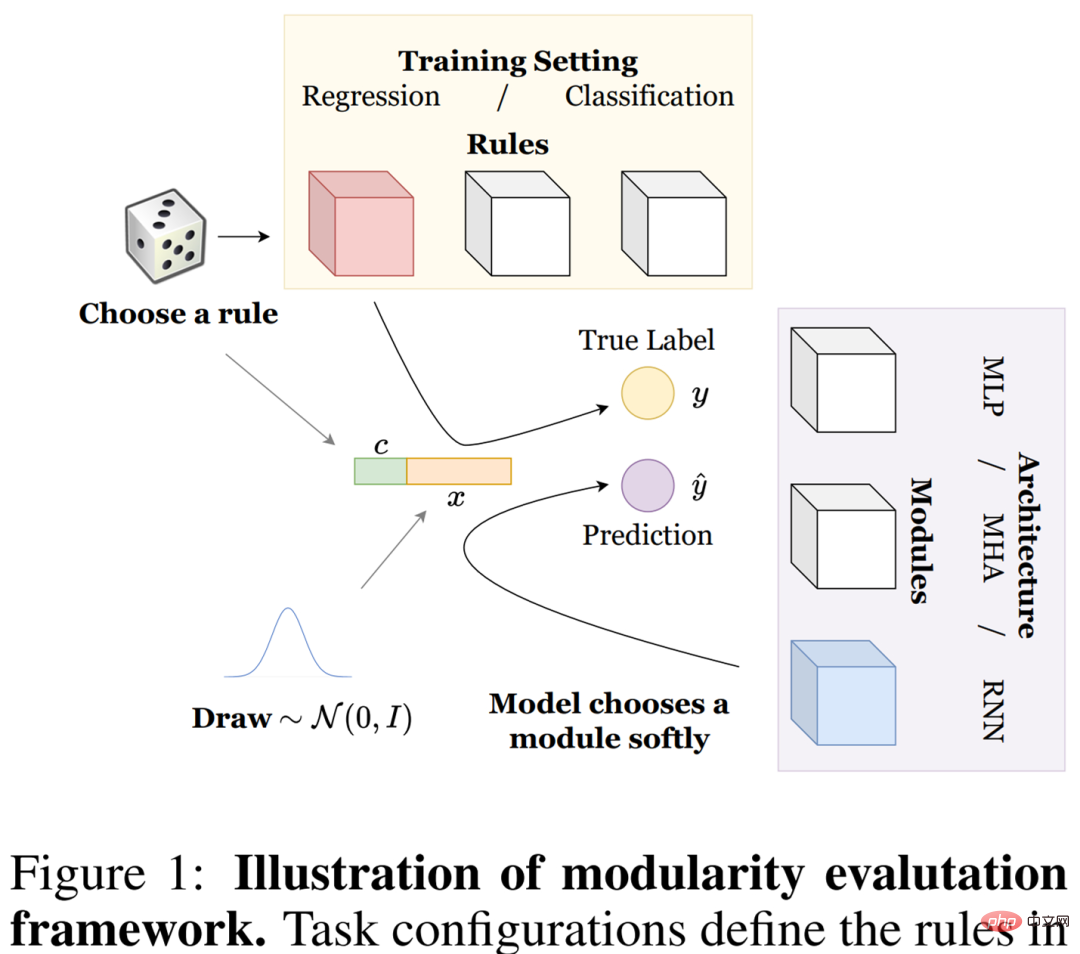
rule. In order to properly understand modular systems and analyze their advantages and disadvantages, the researchers considered a comprehensive setup that allows fine-grained control over different task requirements. In particular, operations, which they call rules, must be learned on the data-generating distributions shown in Equation 1-3 below.
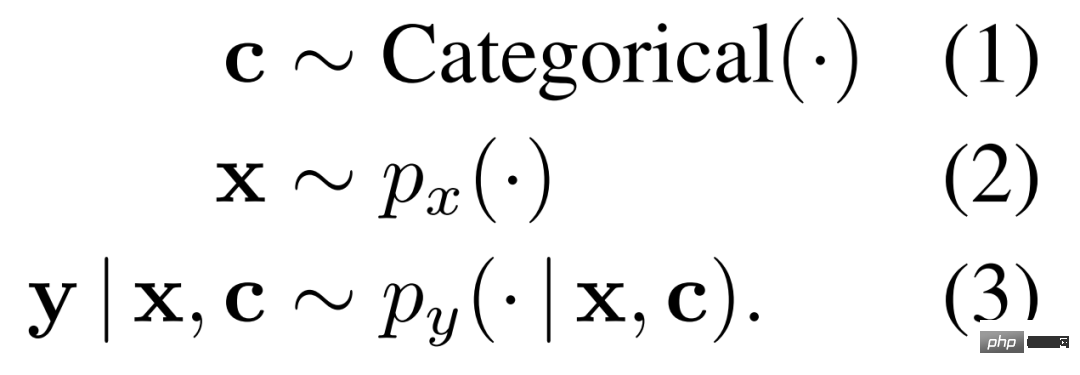
Given the above distribution, the researcher defines a rule to become an expert on it, that is, the rule r is defined as p_y(·|x, c = r), where c is a categorical variable representing context and x is the input sequence.
Task. A task is described by a set of rules (data generating distributions) shown in Equation 1-3. Different sets of {p_y(· | x, c)}_c mean different tasks. For a given number of rules, the model is trained on multiple tasks to eliminate any task-specific bias.
Module. A modular system consists of a set of neural network modules, where each module contributes to the overall output. This can be seen through the following functional form.
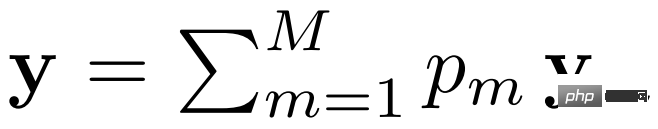
where y_m represents the output and p_m represents the activation of the m^th module.
Model architecture. The model architecture describes what architecture is chosen for each module of a modular system or for individual modules of a monolithic system. In this paper, the researchers consider using multi-layer perceptron (MLP), multi-head attention (MHA) and recurrent neural network (RNN). It is important that the rules (or data-generating distributions) are adapted to fit the model architecture, such as MLP-based rules.
Data generation process
Since the researchers’ goal is to explore modular systems through synthetic data, they introduced in detail the method based on the above Describes the data generation process for the rule scheme. Specifically, the researchers used a simple mixed-of-experts (MoE) style data generation process, hoping that different modules could be specialized for different experts in the rules.
They explain the data generation process for three model architectures, namely MLP, MHA and RNN. Additionally, there are two versions below each task: regression and classification.
MLP. The researchers defined a data scheme suitable for learning based on modular MLP systems. In this synthetic data generation scheme, a data sample consists of two independent numbers and a regular selection sampled from some distribution. Different rules generate different linear combinations of two numbers to give an output, that is, the selection of the linear combination is dynamically instantiated according to the rules, as shown in Equation 4-6 below.
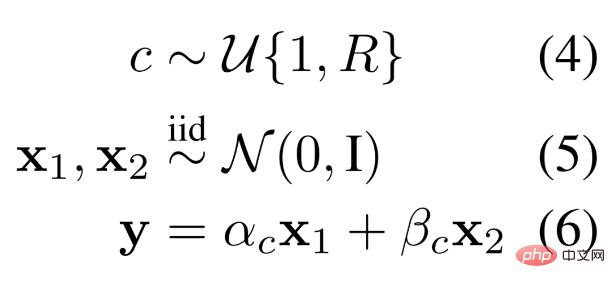

MHA. Now, researchers have defined a data scheme tuned for learning in a modular MHA system. Therefore, they designed a data generation distribution with the following property: each rule consists of different search and retrieval concepts and the final linear combination of retrieved information. Researchers describe this process mathematically in Equation 7-11 below.
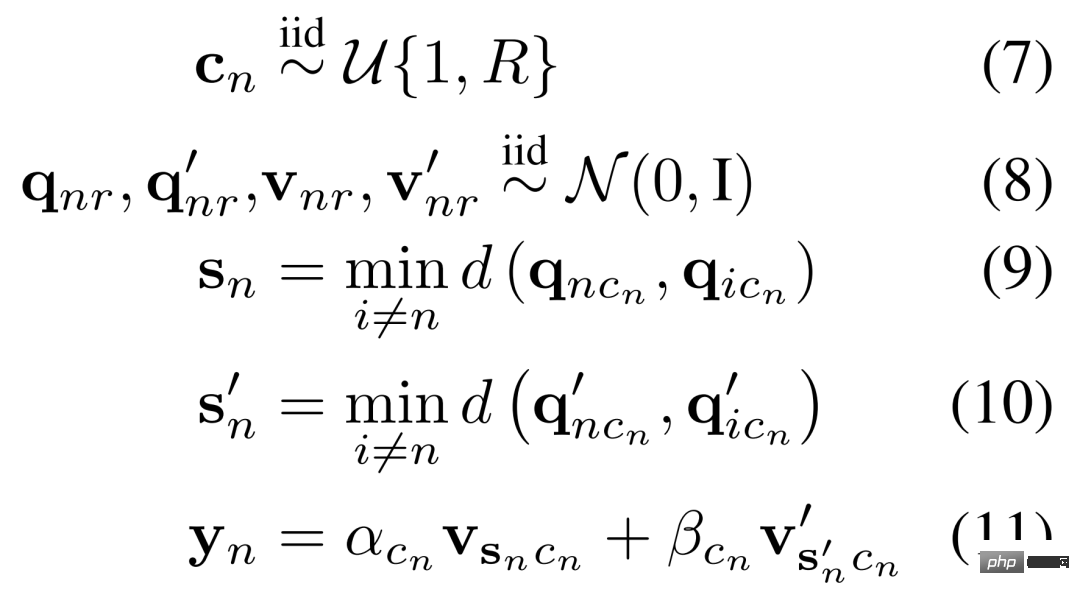
RNN. For circulatory systems, the researchers defined rules for a linear dynamic system in which one of multiple rules can be triggered at any point in time. Mathematically, this process is shown in Equation 12-15 below.
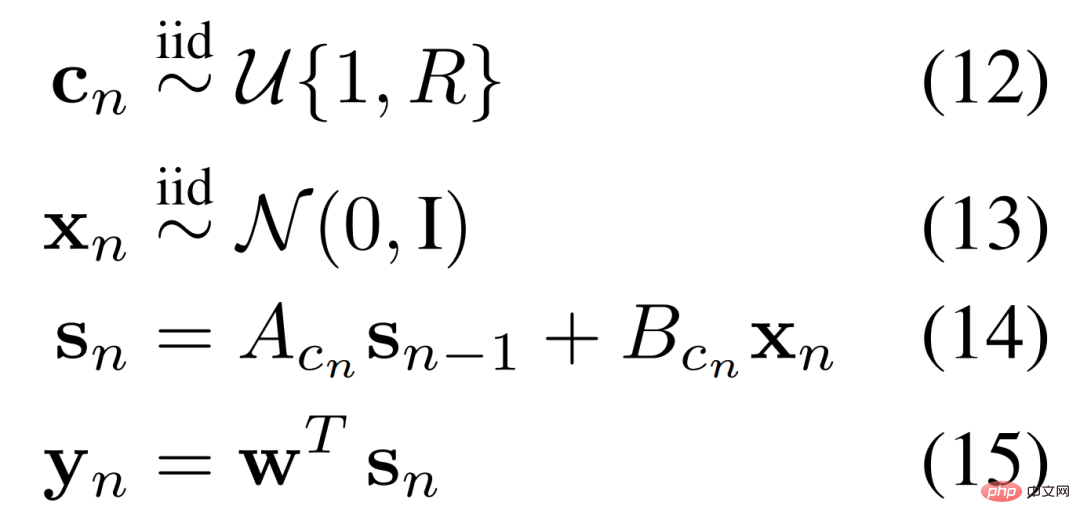
Model
Some previous work claimed that end-to-end trained module systems are superior to single systems, especially in distributed environments. However, there has been no detailed and in-depth analysis of the benefits of these modular systems and whether they actually specialize based on the data generation distribution.
Therefore, the researchers considered four types of models that allow different degrees of specialization, namely Monolithic (single), Modular (modular), Modular-op and GT-Modular . Table 1 below illustrates these models.

Monolithic. A monolithic system is a large neural network that takes as input a whole set of data (x, c) and makes a prediction y^ based on it. The modularity or sparsity of the explicitly baked systems in the system suffers no inductive bias and relies entirely on backpropagation to learn whatever functional form is required to solve the task.
Modular. A modular system consists of many modules, each of which is a neural network of a given architecture type (MLP, MHA, or RNN). Each module m takes data (x, c) as input and computes an output yˆ_m and a confidence score, normalized across modules to the activation probability p_m.
Modular-op. A modular operating system is very similar to a modular system, with one difference. Instead of defining the activation probability p_m of module m as a function of (x, c), the researchers ensured that the activation is determined only by the rule context C.
GT-Modular. True-value modular systems serve as oracle benchmarks, i.e., perfectly specialized modular systems.
Researchers show that from Monolithic to GT-Modular, models increasingly include inductive biases for modularity and sparsity.
Metrics
To reliably evaluate modular systems, researchers have proposed a series of metrics that can not only measure the performance advantages of such systems , and can also be assessed through two important forms: collapse and specialization.
performance. The first set of evaluation metrics is based on performance in both in-distribution and out-of-distribution (OoD) settings, reflecting the performance of different models on various tasks. For the classification setting, we report the classification error; for the regression setting, we report the loss.
collapse. The researchers proposed a set of metrics, Collapse-Avg and Collapse-Worst, to quantify the amount of collapse a modular system encounters (i.e., the extent to which modules are underutilized). Figure 2 below shows an example where you can see that module 3 is not used.
specialization. To complement the collapse metrics, we also propose the following set of metrics, namely (1) alignment, (2) adaptation, and (3) inverse mutual information that quantifies the degree of specialization achieved by a modular system.
Experiment
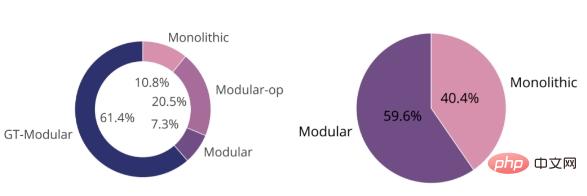
The figure below shows that the GT-Modular system is optimal in most cases (left), which indicates specialization is beneficial. We also see that between the standard end-to-end trained modular system and the monolithic system, the former outperforms the latter but not by much. Together, these two pie charts demonstrate that current modular systems for end-to-end training do not achieve good specialization and are therefore largely suboptimal.

The study then looks at specific architectural choices and analyzes them across a growing set of rules performance and trends.
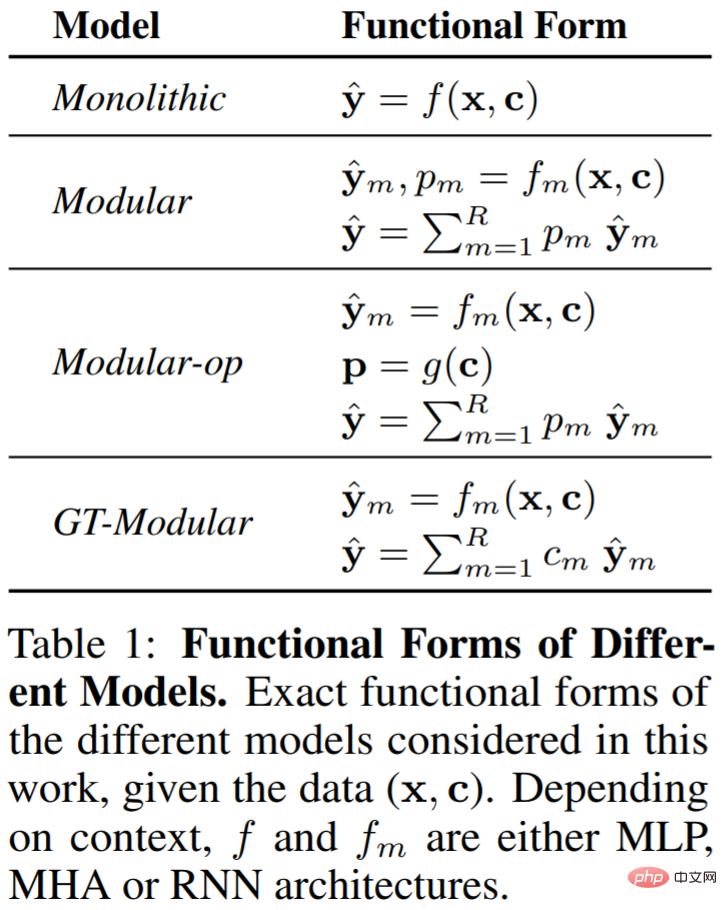
Figure 4 shows that while a perfectly specialized system (GT-Modular) would bring benefits, a typical modular system for end-to-end training is sub-optimal and cannot achieve these benefits, especially as the number of rules increases increase. Furthermore, while such end-to-end modular systems often outperform monolithic systems, the advantage is usually only small.
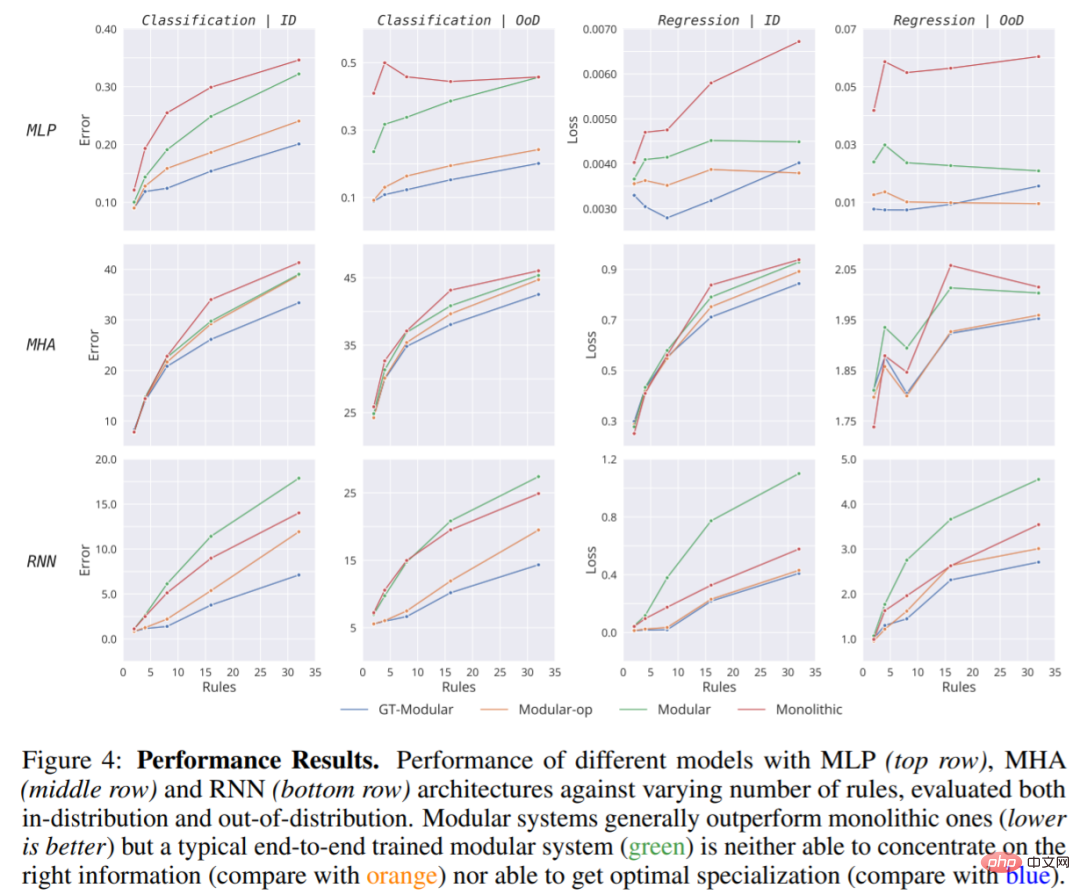
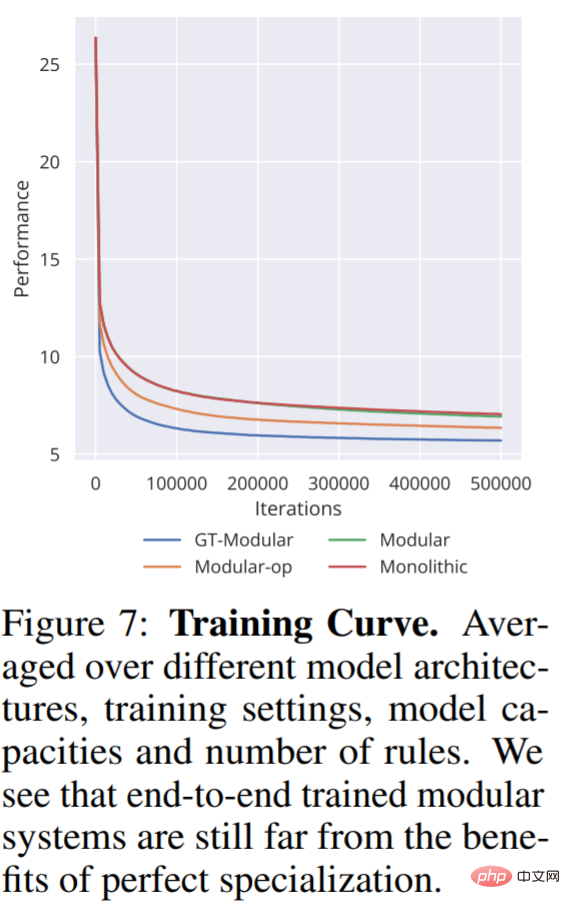
In Figure 7 we also see the average of the training modes for the different models on all other settings, The average includes classification error and regression loss. As can be seen, good specialization not only leads to better performance, but also speeds up training.
The following figure shows two collapse metrics: Collapse-Avg and Collapse-Worst. In addition, the figure below also shows three specialization indicators for different models with different number of rules, alignment, adaptation and inverse mutual information:
 ##
##
The above is the detailed content of Are modular machine learning systems enough? Bengio teachers and students tell you the answer. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
 This article will take you to understand SHAP: model explanation for machine learning
Jun 01, 2024 am 10:58 AM
This article will take you to understand SHAP: model explanation for machine learning
Jun 01, 2024 am 10:58 AM
In the fields of machine learning and data science, model interpretability has always been a focus of researchers and practitioners. With the widespread application of complex models such as deep learning and ensemble methods, understanding the model's decision-making process has become particularly important. Explainable AI|XAI helps build trust and confidence in machine learning models by increasing the transparency of the model. Improving model transparency can be achieved through methods such as the widespread use of multiple complex models, as well as the decision-making processes used to explain the models. These methods include feature importance analysis, model prediction interval estimation, local interpretability algorithms, etc. Feature importance analysis can explain the decision-making process of a model by evaluating the degree of influence of the model on the input features. Model prediction interval estimate
 Huawei's Qiankun ADS3.0 intelligent driving system will be launched in August and will be launched on Xiangjie S9 for the first time
Jul 30, 2024 pm 02:17 PM
Huawei's Qiankun ADS3.0 intelligent driving system will be launched in August and will be launched on Xiangjie S9 for the first time
Jul 30, 2024 pm 02:17 PM
On July 29, at the roll-off ceremony of AITO Wenjie's 400,000th new car, Yu Chengdong, Huawei's Managing Director, Chairman of Terminal BG, and Chairman of Smart Car Solutions BU, attended and delivered a speech and announced that Wenjie series models will be launched this year In August, Huawei Qiankun ADS 3.0 version was launched, and it is planned to successively push upgrades from August to September. The Xiangjie S9, which will be released on August 6, will debut Huawei’s ADS3.0 intelligent driving system. With the assistance of lidar, Huawei Qiankun ADS3.0 version will greatly improve its intelligent driving capabilities, have end-to-end integrated capabilities, and adopt a new end-to-end architecture of GOD (general obstacle identification)/PDP (predictive decision-making and control) , providing the NCA function of smart driving from parking space to parking space, and upgrading CAS3.0
 Identify overfitting and underfitting through learning curves
Apr 29, 2024 pm 06:50 PM
Identify overfitting and underfitting through learning curves
Apr 29, 2024 pm 06:50 PM
This article will introduce how to effectively identify overfitting and underfitting in machine learning models through learning curves. Underfitting and overfitting 1. Overfitting If a model is overtrained on the data so that it learns noise from it, then the model is said to be overfitting. An overfitted model learns every example so perfectly that it will misclassify an unseen/new example. For an overfitted model, we will get a perfect/near-perfect training set score and a terrible validation set/test score. Slightly modified: "Cause of overfitting: Use a complex model to solve a simple problem and extract noise from the data. Because a small data set as a training set may not represent the correct representation of all data." 2. Underfitting Heru
 Transparent! An in-depth analysis of the principles of major machine learning models!
Apr 12, 2024 pm 05:55 PM
Transparent! An in-depth analysis of the principles of major machine learning models!
Apr 12, 2024 pm 05:55 PM
In layman’s terms, a machine learning model is a mathematical function that maps input data to a predicted output. More specifically, a machine learning model is a mathematical function that adjusts model parameters by learning from training data to minimize the error between the predicted output and the true label. There are many models in machine learning, such as logistic regression models, decision tree models, support vector machine models, etc. Each model has its applicable data types and problem types. At the same time, there are many commonalities between different models, or there is a hidden path for model evolution. Taking the connectionist perceptron as an example, by increasing the number of hidden layers of the perceptron, we can transform it into a deep neural network. If a kernel function is added to the perceptron, it can be converted into an SVM. this one
 The evolution of artificial intelligence in space exploration and human settlement engineering
Apr 29, 2024 pm 03:25 PM
The evolution of artificial intelligence in space exploration and human settlement engineering
Apr 29, 2024 pm 03:25 PM
In the 1950s, artificial intelligence (AI) was born. That's when researchers discovered that machines could perform human-like tasks, such as thinking. Later, in the 1960s, the U.S. Department of Defense funded artificial intelligence and established laboratories for further development. Researchers are finding applications for artificial intelligence in many areas, such as space exploration and survival in extreme environments. Space exploration is the study of the universe, which covers the entire universe beyond the earth. Space is classified as an extreme environment because its conditions are different from those on Earth. To survive in space, many factors must be considered and precautions must be taken. Scientists and researchers believe that exploring space and understanding the current state of everything can help understand how the universe works and prepare for potential environmental crises
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Always new! Huawei Mate60 series upgrades to HarmonyOS 4.2: AI cloud enhancement, Xiaoyi Dialect is so easy to use
Jun 02, 2024 pm 02:58 PM
Always new! Huawei Mate60 series upgrades to HarmonyOS 4.2: AI cloud enhancement, Xiaoyi Dialect is so easy to use
Jun 02, 2024 pm 02:58 PM
On April 11, Huawei officially announced the HarmonyOS 4.2 100-machine upgrade plan for the first time. This time, more than 180 devices will participate in the upgrade, covering mobile phones, tablets, watches, headphones, smart screens and other devices. In the past month, with the steady progress of the HarmonyOS4.2 100-machine upgrade plan, many popular models including Huawei Pocket2, Huawei MateX5 series, nova12 series, Huawei Pura series, etc. have also started to upgrade and adapt, which means that there will be More Huawei model users can enjoy the common and often new experience brought by HarmonyOS. Judging from user feedback, the experience of Huawei Mate60 series models has improved in all aspects after upgrading HarmonyOS4.2. Especially Huawei M
 Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Machine learning is an important branch of artificial intelligence that gives computers the ability to learn from data and improve their capabilities without being explicitly programmed. Machine learning has a wide range of applications in various fields, from image recognition and natural language processing to recommendation systems and fraud detection, and it is changing the way we live. There are many different methods and theories in the field of machine learning, among which the five most influential methods are called the "Five Schools of Machine Learning". The five major schools are the symbolic school, the connectionist school, the evolutionary school, the Bayesian school and the analogy school. 1. Symbolism, also known as symbolism, emphasizes the use of symbols for logical reasoning and expression of knowledge. This school of thought believes that learning is a process of reverse deduction, through existing



