 Technology peripherals
Technology peripherals
 AI
AI
 A 30-year historical review, Jeff Dean: We compiled a research review of 'sparse expert models”
A 30-year historical review, Jeff Dean: We compiled a research review of 'sparse expert models”
A 30-year historical review, Jeff Dean: We compiled a research review of 'sparse expert models”
The sparse expert model is a 30-year-old concept that is still widely used today and is a popular architecture in deep learning. Such architectures include hybrid expert systems (MoE), Switch Transformers, routing networks, BASE layers, etc. Sparse expert models have demonstrated good performance in many fields such as natural language processing, computer vision, and speech recognition.
Recently, Jeff Dean, head of Google AI, and others wrote a review of sparse expert models, reviewing the concept of sparse expert models, providing a basic description of general algorithms, and finally looking forward to future research directions.

Paper address: https://arxiv.org/pdf/2209.01667.pdf
Machine learning, especially natural language, has made significant progress by increasing computing budgets, training data, and model sizes. Well-known milestone language models include GPT-2 (Radford et al., 2018), BERT (Devlin et al., 2018), T5 (Raffel et al., 2019), GPT-3 (Brown et al., 2020), Gopher (Rae et al., 2021), Chinchilla (Hoffmann et al., 2022) and PaLM (Chowdhery et al., 2022).
However, state-of-the-art models now require thousands of dedicated interconnected accelerators and take weeks or months to train, making these models expensive to produce (Patterson et al. al., 2021). As machine learning systems scale, the field seeks more efficient training and serving paradigms. Sparse expert models have emerged as a promising solution.
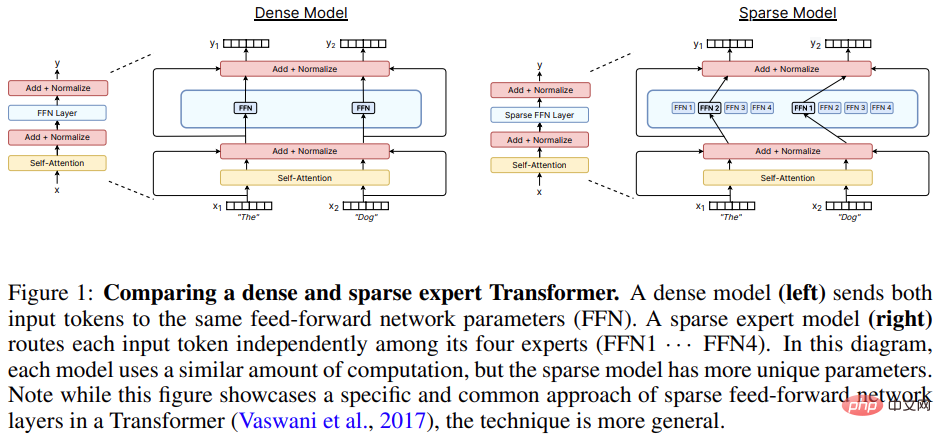
Sparse expert models (of which hybrid expert systems (MoE) are the most popular variant) are a special type of neural network in which a The group parameters are divided into "experts", each with a unique weight.
During training and inference, the model assigns input samples to specific expert weights, allowing each sample to interact with only a subset of the network parameters, as opposed to using the entire network for each The conventional method of input is different. Since only a small number of experts are used for each sample, the computational effort is significantly reduced relative to the total model.
Many modern sparse expert models draw inspiration from Shazeer et al. (2017). The research trained the largest model at the time and achieved state-of-the-art language modeling and translation results. The popularity of sparse expert models has further surged when used in conjunction with Transformer language models (Lepikhin et al., 2020; Fedus et al., 2021). While most work has been in natural language processing, sparse expert models have also been successfully used in a variety of fields, including computer vision (Puigcerver et al., 2020), speech recognition (You et al., 2021), and multimodality learning (Mustafa et al., 2022). Clark et al. (2022) studied the scaling properties of sparse expert models under different model sizes and number of experts. Furthermore, state-of-the-art results on many benchmarks are currently held by sparse expert models such as ST-MoE (Zoph et al., 2022). The field is evolving rapidly with advances in research and engineering.
This review paper narrows the scope of investigation to sparse expert models in the narrow deep learning era (starting in 2012), reviews recent progress and discusses promising future avenues.
Sparse Expert Model
The concept of MoE in machine learning can be traced back to at least 30 years ago. In the early concepts, experts defined a complete neural network ,MoE is similar to an ensemble approach.
Eigen et al. (2013) proposed using a stacked layer expert hybrid architecture on jittered MNIST. This work laid the foundation for the efficient implementation of subsequent models.
Shazeer et al. (2017) proposed inserting a MoE layer between two LSTM layers, and the resulting sparse model achieved SOTA performance in machine translation. However, although this method was successful, subsequent research was like hibernation and stagnated, and most research turned to Transformer.
Between 2020 and 2021, GShard and Switch Transformer were released, both of which replaced the feed-forward layer in Transformer with an expert layer.
Although the approach of using a layer of experts has become the dominant paradigm, research in the past two years has revisited the concept of expert models as completely independent models to achieve modularity and composability sex.
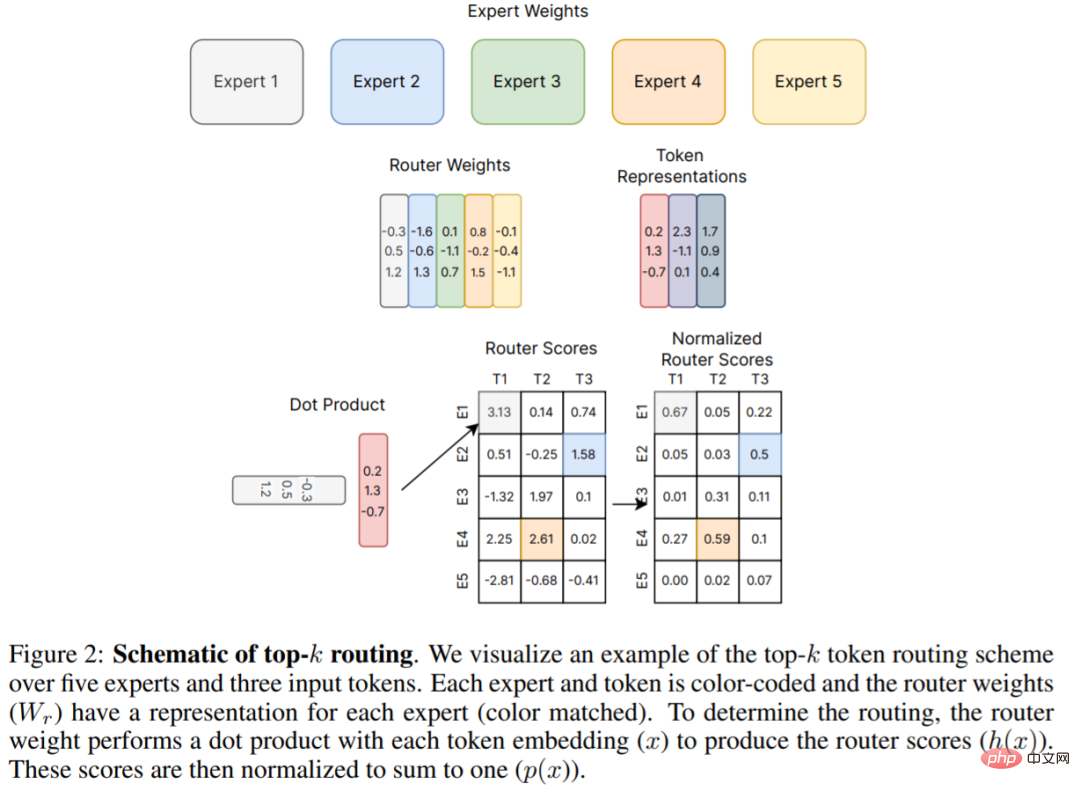
Figure 2 below is the original top-k routing mechanism proposed by Shazeer et al. (2017), which is the basis for many subsequent works. This review paper explains in detail new developments in routing algorithms in Chapter 4.
Hardware
Modern sparse expert models have been developed with Distributed system co-design of neural networks.
Research on large neural networks (Brown et al., 2020; Rae et al., 2021; Chowdhery et al., 2022) shows that neural networks have far exceeded the memory of a single accelerator Capacity, so tensors such as weights, activation functions, optimizer variables, etc. need to be sharded using various parallel strategies.
Three common parallel methods include: data parallelism (copying model weights, sharding data), tensor model parallelism (data and weight tensors are sharded across devices), and pipeline parallelism (whole layers or groups of layers are sharded across devices), hybrid expert models are often able to accommodate these parallelization scenarios.
In terms of training and deployment of MoE models, Jaszczur et al. (2021) sparsified all layers of the Transformer model, thereby achieving 37 times the inference acceleration; Kossmann et al. . (2022) Solving static expert batch size constraints via the RECOMPILE library.
In addition to data parallelism, model parallelism and expert parallelism, Rajbhandari et al. (2022) proposed the DeepSpeed-MoE library to support ZeRO partitioning and ZeRO-Offload, achieving 10x inference Improve and SOTA translation performance, thereby increasing the model's usefulness in production services.
Extended properties of sparse expert models
The cross-entropy loss of dense neural language models behaves as a function of model parameter count, data volume, and computational budget (Kaplan et al ., 2020) power law. The power law coefficients were later corrected in Hoffmann et al. (2022), suggesting that computing the optimal model requires a closer balance of data and parameter expansion. In contrast, early studies of sparse expert models that expanded heuristically obtained strong empirical results but did not carefully describe the expansion laws. Furthermore, some works have highlighted the differences between upstream (e.g. pre-training) and downstream (e.g. fine-tuning) actions (Fedus et al., 2021; Artetxe et al., 2021), further complicating the understanding of sparse expert models.
Upstream extensions
Sparse expert models perform well when trained on large datasets. A common pattern in natural language processing is to first perform upstream training (e.g. pre-training) and then perform downstream training (e.g. fine-tuning) on a specific data distribution of interest. In the upstream stage, sparse expert models consistently yield higher gains than dense counterpart models. Shazeer et al. (2017) proposed scaling curves with respect to model parameters and computational budget on the 1 billion word language modeling benchmark (Chelba et al., 2013), achieving significant gains compared to the dense version. Lepikhin et al. (2020) proposed an improved version of the model expansion function and achieved a BLEU score gain of 13.5 on their largest 600B parameter sparse model. Switch Transformer (Fedus et al., 2021) measured 4-7x wall-time speedup on the T5 model using the same computational resources. The work also investigated scaling the cross-entropy loss as a function of parameter count, but observed that the gains diminished beyond 256 experts.
Downstream Extension
However, reliable upstream scaling did not immediately yield consistent gains on downstream tasks. In a work highlighting the challenges of transfer, Fedus et al. (2021) observed 4x pre-training using a low-compute, high-parameter encoder-decoder Transformer (1.6T parameters, 2048 experts per sparse layer) improvement, but it does not fine-tune well on intensive inference tasks such as SuperGLUE. This finding hints at further necessary research and the balance that may be required between calculations and parameters.
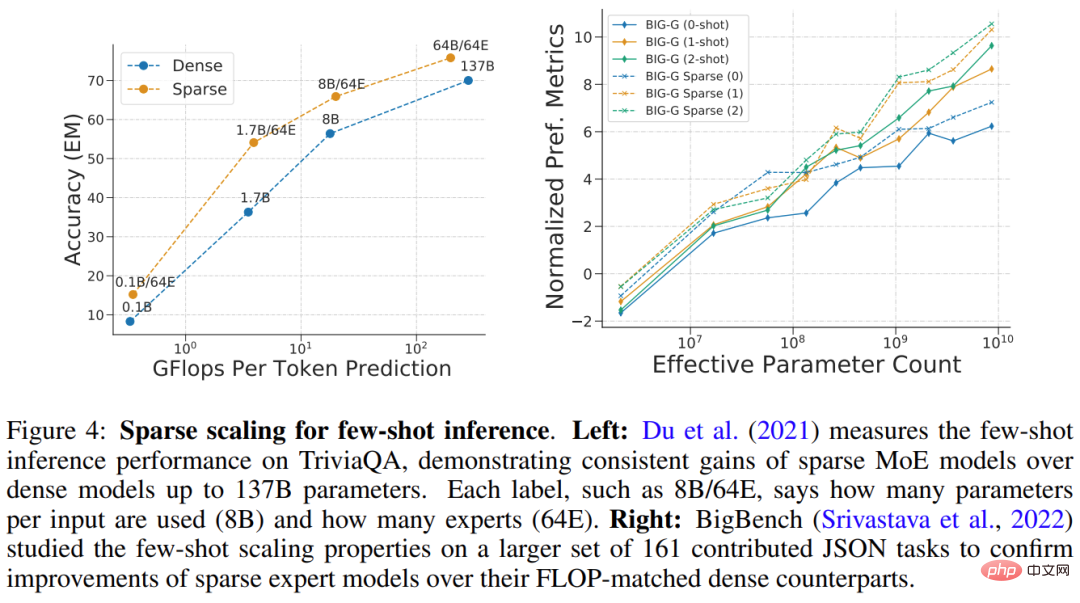
Du et al. (2021) demonstrated an extension of the sparse GLaM model ranging from 1B-64B FLOPs using 64 experts per sparse layer. GLaM achieved SOTA results, outperforming the 175B parameter GPT-3 model (Brown et al., 2020) in terms of zero-shot and one-shot performance. At the same time, the FLOP used by each token during inference was reduced by 49%. The consumption was reduced by 65% (as shown in Figure 4 (left) below). Figure 4 below (right) is another example of a sparse model performing well on few-shot inference.
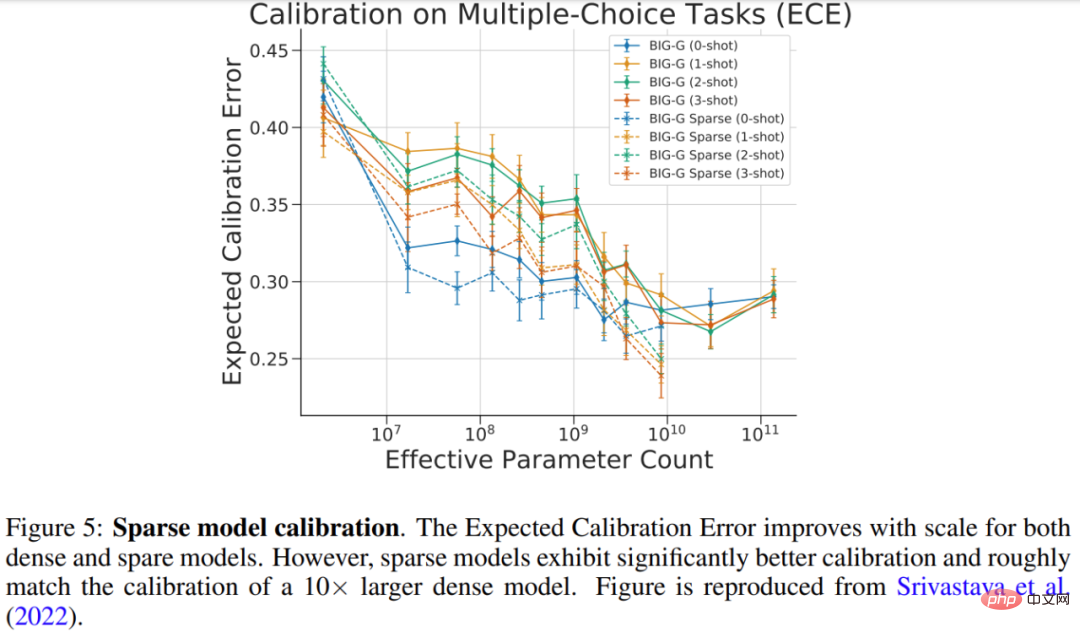
Srivastava et al. (2022) studied the calibration of sparse models on the multiple-choice BIG-Bench task, that is, measuring the predicted probability versus correct The degree of probability matching. The results of the study are shown in Figure 5 below, and while calibration improved for both the larger dense and sparse models, the calibration of the sparse model was comparable to that of the dense model using 10x more FLOPs.
Expand the number, size, and frequency of expert tiers
How many Several important hyperparameters control the scaling of sparse expert models, including: 1) the number of experts, 2) the size of each expert, and 3) the frequency of expert layers. These decisions can have significant impacts on upstream and downstream expansion.
Many early works scaled to thousands of relatively small experts per layer, resulting in excellent pre-training and translation quality (Shazeer et al., 2017; Lepikhin et al ., 2020; Fedus et al., 2021). However, the quality of sparse models degrades disproportionately when domain shifting (Artetxe et al., 2021) or fine-tuning for different task distributions (Fedus et al., 2021). To achieve a better balance of computation and parameters, SOTA sparse models for few-shot inference (GLaM (Du et al., 2021)) and fine-tuning (ST-MoE (Zoph et al., 2022)) can only be used at best. 64 larger experts. Due to the increased expert dimension, these models require specific system-level sharding strategies for accelerators to run effectively (Du et al., 2021; Rajbhandari et al., 2022).
Routing Algorithm
The routing algorithm is a key feature of all sparse expert architectures and determines where to send samples. This area has been extensively studied, including counter-intuitive approaches using fixed, non-learned routing patterns (Roller et al., 2021). Since discrete decisions are made about which experts to select, routing decisions are often non-differentiable.
The expert selection problem was later redefined as the Bandit problem, and there have been some works using reinforcement learning to learn expert selection (Bengio et al., 2016; Rosenbaum et al., 2017; 2019; Clark et al., 2022). Shazeer et al. (2017) proposed a differentiable heuristic algorithm to circumvent the difficulties of reinforcement learning.
This paper elaborates on the classification of routing algorithms and further explains the key issue in this field-load balancing.
The Rapid Development of Sparse Expert Models
The impact of sparse expert models is rapidly spreading to other fields beyond NLP, including computer vision, speech recognition and multi-modal applications . Although the domains are different, the architecture and algorithm of the model are roughly the same, and Table 1 below shows the sparse layer input representation for different domains.

# Sparse expert models have developed very rapidly in recent years. Taking the field of NLP as an example, Shazeer et al. (2017) introduced hybrid expert layers for LSTM language modeling and machine translation, which are inserted between the standard layers of the LSTM model.
In 2020, Lepikhin et al. (2020) introduced the MoE layer to Transformer for the first time. When the researchers expanded each expert layer to 2048 experts, the model achieved SOTA translation on 100 different languages. result.
Fedus et al. (2021) created a sparse 1.6T parameter language model achieving SOTA pre-training quality.
New research is advancing the development of few-shot learning inference and fine-tuning benchmarks. Du et al. (2021) trained a pure MoE decoder language model, achieving SOTA results on small samples and requiring only 1/3 of the computation required to train GPT-3. Zoph et al. (2022) proposed ST-MoE, a sparse encoder-decoder model that achieves SOTA on a wide range of inference and generation tasks. When fine-tuned on SuperGLUE, ST-MoE outperforms PaLM-540B while using only about 1/20th the pre-training FLOPs and 1/40th the inference FLOPs.
When to use sparse models
A common question is that if you are given a fixed compute or FLOP budget (e.g. 100 GPUs for 20 hours), you should What type of model should be trained for best performance?
Fundamentally, sparse models allow for a dramatic increase in the number of parameters in the model by increasing the number of experts, while keeping the FLOP per sample roughly constant. This approach can be good or bad, depending on the purpose of the model.
Sparsity is beneficial when you have many accelerators (e.g. GPU/TPU) to carry all the additional parameters that come with using sparsity.
Using sparsity also requires careful consideration of downstream tasks. If you have many machines for pretraining but few for fine-tuning or serving, then the sparsity (e.g. number of experts) should be adjusted based on the amount of memory available in downstream use cases.
In some cases, sparse models always look worse than dense models. For example, when all parameters are stored in the accelerator memory, a sparse model is inferior to a dense model. Sparse models are ideal when you have the ability to train or serve in parallel on multiple machines in order to host additional model parameters from experts.
In addition, this review paper also introduces the improvement of sparse model training, interpretability and future research directions. Interested friends can check the original paper to learn more research content.
The above is the detailed content of A 30-year historical review, Jeff Dean: We compiled a research review of 'sparse expert models”. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1385
1385
 52
52
 The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
May 07, 2024 pm 04:13 PM
The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
May 07, 2024 pm 04:13 PM
Imagine an artificial intelligence model that not only has the ability to surpass traditional computing, but also achieves more efficient performance at a lower cost. This is not science fiction, DeepSeek-V2[1], the world’s most powerful open source MoE model is here. DeepSeek-V2 is a powerful mixture of experts (MoE) language model with the characteristics of economical training and efficient inference. It consists of 236B parameters, 21B of which are used to activate each marker. Compared with DeepSeek67B, DeepSeek-V2 has stronger performance, while saving 42.5% of training costs, reducing KV cache by 93.3%, and increasing the maximum generation throughput to 5.76 times. DeepSeek is a company exploring general artificial intelligence
 AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI is indeed changing mathematics. Recently, Tao Zhexuan, who has been paying close attention to this issue, forwarded the latest issue of "Bulletin of the American Mathematical Society" (Bulletin of the American Mathematical Society). Focusing on the topic "Will machines change mathematics?", many mathematicians expressed their opinions. The whole process was full of sparks, hardcore and exciting. The author has a strong lineup, including Fields Medal winner Akshay Venkatesh, Chinese mathematician Zheng Lejun, NYU computer scientist Ernest Davis and many other well-known scholars in the industry. The world of AI has changed dramatically. You know, many of these articles were submitted a year ago.
 Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
Apr 01, 2024 pm 07:46 PM
Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
Apr 01, 2024 pm 07:46 PM
The performance of JAX, promoted by Google, has surpassed that of Pytorch and TensorFlow in recent benchmark tests, ranking first in 7 indicators. And the test was not done on the TPU with the best JAX performance. Although among developers, Pytorch is still more popular than Tensorflow. But in the future, perhaps more large models will be trained and run based on the JAX platform. Models Recently, the Keras team benchmarked three backends (TensorFlow, JAX, PyTorch) with the native PyTorch implementation and Keras2 with TensorFlow. First, they select a set of mainstream
 Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
Apr 18, 2024 pm 07:58 PM
Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas officially enters the era of electric robots! Yesterday, the hydraulic Atlas just "tearfully" withdrew from the stage of history. Today, Boston Dynamics announced that the electric Atlas is on the job. It seems that in the field of commercial humanoid robots, Boston Dynamics is determined to compete with Tesla. After the new video was released, it had already been viewed by more than one million people in just ten hours. The old people leave and new roles appear. This is a historical necessity. There is no doubt that this year is the explosive year of humanoid robots. Netizens commented: The advancement of robots has made this year's opening ceremony look like a human, and the degree of freedom is far greater than that of humans. But is this really not a horror movie? At the beginning of the video, Atlas is lying calmly on the ground, seemingly on his back. What follows is jaw-dropping
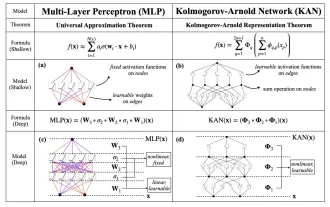 KAN, which replaces MLP, has been extended to convolution by open source projects
Jun 01, 2024 pm 10:03 PM
KAN, which replaces MLP, has been extended to convolution by open source projects
Jun 01, 2024 pm 10:03 PM
Earlier this month, researchers from MIT and other institutions proposed a very promising alternative to MLP - KAN. KAN outperforms MLP in terms of accuracy and interpretability. And it can outperform MLP running with a larger number of parameters with a very small number of parameters. For example, the authors stated that they used KAN to reproduce DeepMind's results with a smaller network and a higher degree of automation. Specifically, DeepMind's MLP has about 300,000 parameters, while KAN only has about 200 parameters. KAN has a strong mathematical foundation like MLP. MLP is based on the universal approximation theorem, while KAN is based on the Kolmogorov-Arnold representation theorem. As shown in the figure below, KAN has
 Time Series Forecasting NLP Large Model New Work: Automatically Generate Implicit Prompts for Time Series Forecasting
Mar 18, 2024 am 09:20 AM
Time Series Forecasting NLP Large Model New Work: Automatically Generate Implicit Prompts for Time Series Forecasting
Mar 18, 2024 am 09:20 AM
Today I would like to share a recent research work from the University of Connecticut that proposes a method to align time series data with large natural language processing (NLP) models on the latent space to improve the performance of time series forecasting. The key to this method is to use latent spatial hints (prompts) to enhance the accuracy of time series predictions. Paper title: S2IP-LLM: SemanticSpaceInformedPromptLearningwithLLMforTimeSeriesForecasting Download address: https://arxiv.org/pdf/2403.05798v1.pdf 1. Large problem background model
 Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!
May 06, 2024 pm 04:13 PM
Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!
May 06, 2024 pm 04:13 PM
The latest video of Tesla's robot Optimus is released, and it can already work in the factory. At normal speed, it sorts batteries (Tesla's 4680 batteries) like this: The official also released what it looks like at 20x speed - on a small "workstation", picking and picking and picking: This time it is released One of the highlights of the video is that Optimus completes this work in the factory, completely autonomously, without human intervention throughout the process. And from the perspective of Optimus, it can also pick up and place the crooked battery, focusing on automatic error correction: Regarding Optimus's hand, NVIDIA scientist Jim Fan gave a high evaluation: Optimus's hand is the world's five-fingered robot. One of the most dexterous. Its hands are not only tactile
 FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
Target detection is a relatively mature problem in autonomous driving systems, among which pedestrian detection is one of the earliest algorithms to be deployed. Very comprehensive research has been carried out in most papers. However, distance perception using fisheye cameras for surround view is relatively less studied. Due to large radial distortion, standard bounding box representation is difficult to implement in fisheye cameras. To alleviate the above description, we explore extended bounding box, ellipse, and general polygon designs into polar/angular representations and define an instance segmentation mIOU metric to analyze these representations. The proposed model fisheyeDetNet with polygonal shape outperforms other models and simultaneously achieves 49.5% mAP on the Valeo fisheye camera dataset for autonomous driving



