
Deep Deterministic Policy Gradient (DDPG) is a model-free, non-policy deep reinforcement algorithm inspired by Deep Q-Network. It is based on Actor-Critic using policy gradient. This article will use pytorch to perform it. Complete implementation and explanation

The key component of DDPG is
Let’s implement it step by step:
DDPG uses Replay Buffer to store the process and rewards (Sₜ, aₜ, Rₜ, Sₜ ₁) sampled by exploring the environment. Replay Buffer plays a vital role in helping the agent accelerate learning and the stability of DDPG:
class Replay_buffer(): ''' Code based on: https://github.com/openai/baselines/blob/master/baselines/deepq/replay_buffer.py Expects tuples of (state, next_state, action, reward, done) ''' def __init__(self, max_size=capacity): """Create Replay buffer. Parameters ---------- size: int Max number of transitions to store in the buffer. When the buffer overflows the old memories are dropped. """ self.storage = [] self.max_size = max_size self.ptr = 0 def push(self, data): if len(self.storage) == self.max_size: self.storage[int(self.ptr)] = data self.ptr = (self.ptr + 1) % self.max_size else: self.storage.append(data) def sample(self, batch_size): """Sample a batch of experiences. Parameters ---------- batch_size: int How many transitions to sample. Returns ------- state: np.array batch of state or observations action: np.array batch of actions executed given a state reward: np.array rewards received as results of executing action next_state: np.array next state next state or observations seen after executing action done: np.array done[i] = 1 if executing ation[i] resulted in the end of an episode and 0 otherwise. """ ind = np.random.randint(0, len(self.storage), size=batch_size) state, next_state, action, reward, done = [], [], [], [], [] for i in ind: st, n_st, act, rew, dn = self.storage[i] state.append(np.array(st, copy=False)) next_state.append(np.array(n_st, copy=False)) action.append(np.array(act, copy=False)) reward.append(np.array(rew, copy=False)) done.append(np.array(dn, copy=False)) return np.array(state), np.array(next_state), np.array(action), np.array(reward).reshape(-1, 1), np.array(done).reshape(-1, 1)
This is the PyTorch implementation of the Actor-Critic reinforcement learning algorithm. This code defines two neural network models, an Actor and a Critic.
The input of the Actor model: environment state; the output of the Actor model: actions with continuous values.
The input of the Critic model: environmental state and action; the output of the Critic model: Q value, which is the expected total reward of the current state-action pair.
class Actor(nn.Module): """ The Actor model takes in a state observation as input and outputs an action, which is a continuous value. It consists of four fully connected linear layers with ReLU activation functions and a final output layer selects one single optimized action for the state """ def __init__(self, n_states, action_dim, hidden1): super(Actor, self).__init__() self.net = nn.Sequential( nn.Linear(n_states, hidden1), nn.ReLU(), nn.Linear(hidden1, hidden1), nn.ReLU(), nn.Linear(hidden1, hidden1), nn.ReLU(), nn.Linear(hidden1, 1) ) def forward(self, state): return self.net(state) class Critic(nn.Module): """ The Critic model takes in both a state observation and an action as input and outputs a Q-value, which estimates the expected total reward for the current state-action pair. It consists of four linear layers with ReLU activation functions, State and action inputs are concatenated before being fed into the first linear layer. The output layer has a single output, representing the Q-value """ def __init__(self, n_states, action_dim, hidden2): super(Critic, self).__init__() self.net = nn.Sequential( nn.Linear(n_states + action_dim, hidden2), nn.ReLU(), nn.Linear(hidden2, hidden2), nn.ReLU(), nn.Linear(hidden2, hidden2), nn.ReLU(), nn.Linear(hidden2, action_dim) ) def forward(self, state, action): return self.net(torch.cat((state, action), 1))
Adding noise to the actions selected by an Actor is a technique used in DDPG to encourage exploration and improve the learning process.
Gaussian noise or Ornstein-Uhlenbeck noise can be used. Gaussian noise is simple and easy to implement, and Ornstein-Uhlenbeck noise generates time-correlated noise that can help agents explore action space more efficiently. But the Ornstein-Uhlenbeck noise fluctuations are smoother and less random than the Gaussian noise method.
import numpy as np import random import copy class OU_Noise(object): """Ornstein-Uhlenbeck process. code from : https://math.stackexchange.com/questions/1287634/implementing-ornstein-uhlenbeck-in-matlab The OU_Noise class has four attributes size: the size of the noise vector to be generated mu: the mean of the noise, set to 0 by default theta: the rate of mean reversion, controlling how quickly the noise returns to the mean sigma: the volatility of the noise, controlling the magnitude of fluctuations """ def __init__(self, size, seed, mu=0., theta=0.15, sigma=0.2): self.mu = mu * np.ones(size) self.theta = theta self.sigma = sigma self.seed = random.seed(seed) self.reset() def reset(self): """Reset the internal state (= noise) to mean (mu).""" self.state = copy.copy(self.mu) def sample(self): """Update internal state and return it as a noise sample. This method uses the current state of the noise and generates the next sample """ dx = self.theta * (self.mu - self.state) + self.sigma * np.array([np.random.normal() for _ in range(len(self.state))]) self.state += dx return self.state
To use Gaussian noise in DDPG, you can add Gaussian noise directly to the agent's action selection process.
DDPG (Deep Deterministic Policy Gradient) uses two sets of Actor-Critic neural networks for function approximation. In DDPG, the target network is Actor-Critic, which has the same structure and parameterization as the Actor-Critic network.
During the training period, the agent uses its Actor-Critic network to interact with the environment and stores experience tuples (Sₜ, Aₜ, Rₜ, Sₜ ₁) in the Replay Buffer. The agent then samples from the Replay Buffer and updates the Actor-Critic network with the data. Rather than updating the target network weights by copying directly from the Actor-Critic network, the DDPG algorithm slowly updates the target network weights through a process called soft target updating.
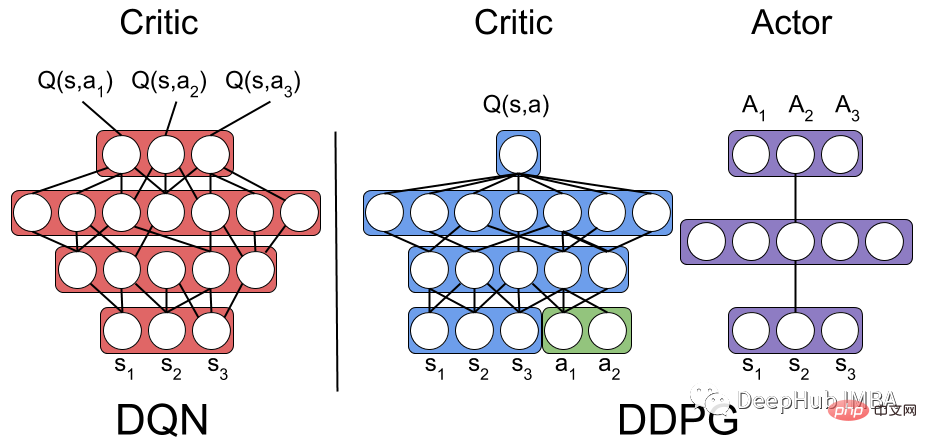
Soft targets are updated as a fraction of the weights transferred from the Actor-Critic network to the target network called the target update rate (τ) .
The update formula of the soft target is as follows:
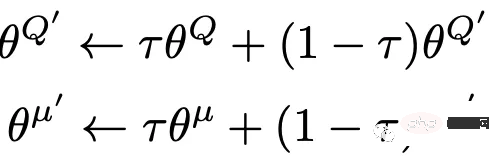
By using soft target technology, the stability of learning can be greatly improved.
#Set Hyperparameters # Hyperparameters adapted for performance from capacity=1000000 batch_size=64 update_iteration=200 tau=0.001 # tau for soft updating gamma=0.99 # discount factor directory = './' hidden1=20 # hidden layer for actor hidden2=64. #hiiden laye for critic class DDPG(object): def __init__(self, state_dim, action_dim): """ Initializes the DDPG agent. Takes three arguments: state_dim which is the dimensionality of the state space, action_dim which is the dimensionality of the action space, and max_action which is the maximum value an action can take. Creates a replay buffer, an actor-critic networks and their corresponding target networks. It also initializes the optimizer for both actor and critic networks alog with counters to track the number of training iterations. """ self.replay_buffer = Replay_buffer() self.actor = Actor(state_dim, action_dim, hidden1).to(device) self.actor_target = Actor(state_dim, action_dim,hidden1).to(device) self.actor_target.load_state_dict(self.actor.state_dict()) self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=3e-3) self.critic = Critic(state_dim, action_dim,hidden2).to(device) self.critic_target = Critic(state_dim, action_dim,hidden2).to(device) self.critic_target.load_state_dict(self.critic.state_dict()) self.critic_optimizer = optim.Adam(self.critic.parameters(), lr=2e-2) # learning rate self.num_critic_update_iteration = 0 self.num_actor_update_iteration = 0 self.num_training = 0 def select_action(self, state): """ takes the current state as input and returns an action to take in that state. It uses the actor network to map the state to an action. """ state = torch.FloatTensor(state.reshape(1, -1)).to(device) return self.actor(state).cpu().data.numpy().flatten() def update(self): """ updates the actor and critic networks using a batch of samples from the replay buffer. For each sample in the batch, it computes the target Q value using the target critic network and the target actor network. It then computes the current Q value using the critic network and the action taken by the actor network. It computes the critic loss as the mean squared error between the target Q value and the current Q value, and updates the critic network using gradient descent. It then computes the actor loss as the negative mean Q value using the critic network and the actor network, and updates the actor network using gradient ascent. Finally, it updates the target networks using soft updates, where a small fraction of the actor and critic network weights are transferred to their target counterparts. This process is repeated for a fixed number of iterations. """ for it in range(update_iteration): # For each Sample in replay buffer batch state, next_state, action, reward, done = self.replay_buffer.sample(batch_size) state = torch.FloatTensor(state).to(device) action = torch.FloatTensor(action).to(device) next_state = torch.FloatTensor(next_state).to(device) done = torch.FloatTensor(1-done).to(device) reward = torch.FloatTensor(reward).to(device) # Compute the target Q value target_Q = self.critic_target(next_state, self.actor_target(next_state)) target_Q = reward + (done * gamma * target_Q).detach() # Get current Q estimate current_Q = self.critic(state, action) # Compute critic loss critic_loss = F.mse_loss(current_Q, target_Q) # Optimize the critic self.critic_optimizer.zero_grad() critic_loss.backward() self.critic_optimizer.step() # Compute actor loss as the negative mean Q value using the critic network and the actor network actor_loss = -self.critic(state, self.actor(state)).mean() # Optimize the actor self.actor_optimizer.zero_grad() actor_loss.backward() self.actor_optimizer.step() """ Update the frozen target models using soft updates, where tau,a small fraction of the actor and critic network weights are transferred to their target counterparts. """ for param, target_param in zip(self.critic.parameters(), self.critic_target.parameters()): target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data) for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()): target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data) self.num_actor_update_iteration += 1 self.num_critic_update_iteration += 1 def save(self): """ Saves the state dictionaries of the actor and critic networks to files """ torch.save(self.actor.state_dict(), directory + 'actor.pth') torch.save(self.critic.state_dict(), directory + 'critic.pth') def load(self): """ Loads the state dictionaries of the actor and critic networks to files """ self.actor.load_state_dict(torch.load(directory + 'actor.pth')) self.critic.load_state_dict(torch.load(directory + 'critic.pth'))
Here we use OpenAI Gym’s “MountainCarContinuous-v0” to train our DDPG RL model. The environment here provides a continuous action and observation space. The goal is to make the car as soon as possible Reach the top of the mountain.
The various parameters of the algorithm are defined below, such as the maximum number of training times, exploration noise, recording interval, etc. Using a fixed random seed allows the process to be backtracked.
import gym # create the environment env_name='MountainCarContinuous-v0' env = gym.make(env_name) device = 'cuda' if torch.cuda.is_available() else 'cpu' # Define different parameters for training the agent max_episode=100 max_time_steps=5000 ep_r = 0 total_step = 0 score_hist=[] # for rensering the environmnet render=True render_interval=10 # for reproducibility env.seed(0) torch.manual_seed(0) np.random.seed(0) #Environment action ans states state_dim = env.observation_space.shape[0] action_dim = env.action_space.shape[0] max_action = float(env.action_space.high[0]) min_Val = torch.tensor(1e-7).float().to(device) # Exploration Noise exploration_noise=0.1 exploration_noise=0.1 * max_action
Create an instance of the DDPG agent class to train the agent for the specified number of times. The agent's update() method is called at the end of each round to update the parameters, and the save() method is used after every ten rounds to save the agent's parameters to a file.
# Create a DDPG instance
agent = DDPG(state_dim, action_dim)
# Train the agent for max_episodes
for i in range(max_episode):
total_reward = 0
step =0
state = env.reset()
fort in range(max_time_steps):
action = agent.select_action(state)
# Add Gaussian noise to actions for exploration
action = (action + np.random.normal(0, 1, size=action_dim)).clip(-max_action, max_action)
#action += ou_noise.sample()
next_state, reward, done, info = env.step(action)
total_reward += reward
if render and i >= render_interval : env.render()
agent.replay_buffer.push((state, next_state, action, reward, np.float(done)))
state = next_state
if done:
break
step += 1
score_hist.append(total_reward)
total_step += step+1
print("Episode: t{} Total Reward: t{:0.2f}".format( i, total_reward))
agent.update()
if i % 10 == 0:
agent.save()
env.close()test_iteration=100
for i in range(test_iteration):
state = env.reset()
for t in count():
action = agent.select_action(state)
next_state, reward, done, info = env.step(np.float32(action))
ep_r += reward
print(reward)
env.render()
if done:
print("reward{}".format(reward))
print("Episode t{}, the episode reward is t{:0.2f}".format(i, ep_r))
ep_r = 0
env.render()
break
state = next_stateWe use the following parameters to make the model converge:
The effect after training for 75 rounds is as follows:
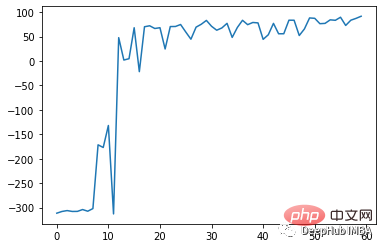
The DDPG algorithm is a model-free off-policy Actor-Critic algorithm inspired by the deep Q-Network (DQN) algorithm. It combines the advantages of policy gradient methods and Q-learning to learn deterministic policies in continuous action spaces.
Similar to DQN, it uses a replay buffer to store past experience and target networks for training the network, thereby improving the stability of the training process.
The DDPG algorithm requires careful hyperparameter tuning for optimal performance. Hyperparameters include learning rate, batch size, target network update rate, and detection noise parameters. Small changes in hyperparameters can have a significant impact on the performance of the algorithm.
The above is the detailed content of PyTorch code implementation and step-by-step explanation of DDPG reinforcement learning. For more information, please follow other related articles on the PHP Chinese website!




