 Technology peripherals
Technology peripherals
 AI
AI
 Poisson matrix decomposition: A matrix decomposition algorithm that solves the cold start problem of recommendation systems without data
Poisson matrix decomposition: A matrix decomposition algorithm that solves the cold start problem of recommendation systems without data
Poisson matrix decomposition: A matrix decomposition algorithm that solves the cold start problem of recommendation systems without data
Author | Wang Hao
Reviewer | Sun Shujuan
The recommendation system is one of the most popular technologies in the Internet industry. In the past decade, the Internet industry has produced millions of iterative versions of recommendation system models. Although there are many recommendation system models optimized for different scenarios, there are very few classic models. Matrix decomposition is a recommendation system algorithm that emerged in the early days of the field of recommendation systems and showed its prominence in the Netflix competition. It is also the most successful recommendation system algorithm in the past ten years. Although as of today in 2023, the field of recommendation systems has long been dominated by deep learning, matrix decomposition is still widely used in the research and development processes of major companies, and there are still many scientific researchers working on related algorithms.

The most classic paper on matrix factorization algorithm is the 2007 Probabilistic Matrix Factorization. On this basis, later generations have carried out a lot of expansion work, such as RankMat in 2021 (paper download address: https://arxiv.org/abs/2204.13016), ZeroMat (paper download address: https://arxiv.org /abs/2112.03084) and DotMat in 2022 (paper download address: https://arxiv.org/abs/2206.00151), KL-Mat (paper download address: https://arxiv.org/abs/2204.13583/ code download Address: https://github.com/haow85/KL-Mat), etc. Recommendation systems are deeply loved by engineers in the Internet industry because of their simplicity, ease of use, and fast speed.
The cold start problem of recommendation systems is another research hotspot that has attracted much attention this year. Many practitioners' ideas for solving recommendation systems are transfer learning and meta-learning. However, this idea has a fatal flaw, which is that it requires data from other knowledge fields. Many companies do not meet this condition. The cold start algorithm, which really does not require any data, appeared after ZeroMat was proposed in 2021. Representative algorithms include ZeroMat and DotMat mentioned in the previous section. The Poisson matrix decomposition algorithm (PoissonMat) to be introduced in this article is a paper published at the 2022 International Academic Conference MLISE 2022. The name of the paper is PoissonMat: Remodeling Matrix Factorization using Poisson Distribution and Solving the Cold Start Problem without Input Data (paper download address: https://arxiv.org/abs/2212.10460).
Let’s first review the MAP definition of Probabilistic Matrix Factorization:
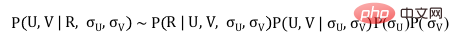
We then define the behavior of users to score items as MAP loosely distributed. According to the definition of Poisson distribution, we get the following formula:
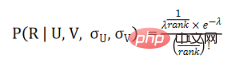
According to the definition of parameters in Poisson formula, we have:

According to the Zipf distribution, we can get the following formula:
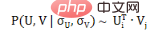
Based on the above Formula, we get the analytical form of Poisson matrix decomposition (PoissonMat):

Using the stochastic gradient descent algorithm to solve the above formula, we get the following algorithm flow :

The author then conducted an experimental comparison of algorithm accuracy and fairness on MovieLens 1 Million Dataset and LDOS-CoMoDa Dataset:
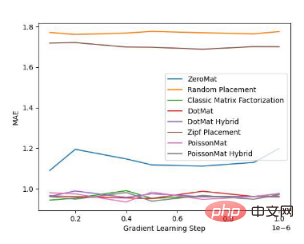
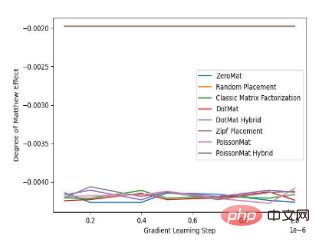
Figure 1 Comparative experiment of Poisson matrix decomposition on MovieLens 1 Million Dataset
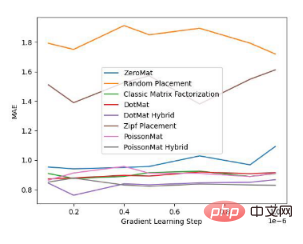
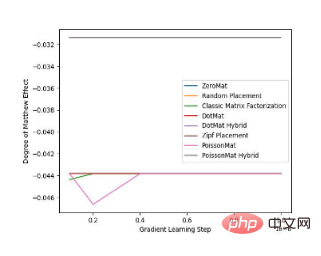
Figure 2 Comparative experiment of Poisson matrix decomposition on LDOS-CoMoDa Dataset
According to the experimental comparison results, we can draw the following conclusions : Poisson matrix factorization (PoissonMat) outperforms other algorithms in both accuracy and fairness metrics. What is commendable is that the Poisson matrix decomposition algorithm does not use any input data and is a complete zero-shot learning algorithm, which solves the cold start problem well.
Finally, the author did the experiment on a Lenovo home notebook with 16G RAM and Intel Core i5. The algorithm runs very fast and the implementation is very simple.
The zero-shot learning algorithm, which aims to solve the cold start problem of recommendation systems, is currently a research hotspot. A true zero-shot learning algorithm that does not require any data to solve zero-shot learning problems, starting from the ZeroMat algorithm in 2021. The Poisson matrix decomposition algorithm (PoissonMat) introduced in this article performs better than ZeroMat and its subsequent algorithm DotMat, and is currently one of the best algorithms in this field. Since the relevant research is still in its infancy, we hope it will attract the attention and attention of the majority of science and technology practitioners.
Introduction to the author
Wang Hao, former head of Funplus Artificial Intelligence Laboratory, former head of Hengchang Litong Big Data Department. Graduated from the University of Utah in the United States with a bachelor's degree (2008) and a master's degree (2010). Part-time MBA from University of International Business and Economics (2016). In recommendation systems (fairness/scenario-based recommendation/cold start/interpretability/ranking learning), computer graphics (geometric modeling/visualization), natural language processing (implementation applications in industry), risk control and anti-fraud ( Finance/medical) and other directions with many years of experience and unique insights. He has 12 years of technology R&D and management experience in the Internet (Douban, Baidu, Sina, NetEase, etc.), financial technology (Hengchang Litong) and gaming companies (Funplus, etc.). Published 30 papers in international academic conferences and journals, and won 3 international conference Best Paper Awards/Best Paper Report Awards (IEEE SMI 2008 Best Paper Award/ICBDT 2020 Best Oral Presentation Award/ICISCAE 2021 Best Oral Presentation Award). 2006 ACM/ICPC North American Rocky Mountain Regional Competition Gold Medal. 2004 Bronze Medal in the Speaking Final of the National College English Proficiency Competition. In 2003, he won the first place in English in science and engineering in Jinan College Entrance Examination.
The above is the detailed content of Poisson matrix decomposition: A matrix decomposition algorithm that solves the cold start problem of recommendation systems without data. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
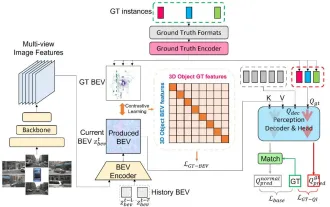 CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
Written above & the author’s personal understanding: At present, in the entire autonomous driving system, the perception module plays a vital role. The autonomous vehicle driving on the road can only obtain accurate perception results through the perception module. The downstream regulation and control module in the autonomous driving system makes timely and correct judgments and behavioral decisions. Currently, cars with autonomous driving functions are usually equipped with a variety of data information sensors including surround-view camera sensors, lidar sensors, and millimeter-wave radar sensors to collect information in different modalities to achieve accurate perception tasks. The BEV perception algorithm based on pure vision is favored by the industry because of its low hardware cost and easy deployment, and its output results can be easily applied to various downstream tasks.
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
The bottom layer of the C++sort function uses merge sort, its complexity is O(nlogn), and provides different sorting algorithm choices, including quick sort, heap sort and stable sort.
 Can artificial intelligence predict crime? Explore CrimeGPT's capabilities
Mar 22, 2024 pm 10:10 PM
Can artificial intelligence predict crime? Explore CrimeGPT's capabilities
Mar 22, 2024 pm 10:10 PM
The convergence of artificial intelligence (AI) and law enforcement opens up new possibilities for crime prevention and detection. The predictive capabilities of artificial intelligence are widely used in systems such as CrimeGPT (Crime Prediction Technology) to predict criminal activities. This article explores the potential of artificial intelligence in crime prediction, its current applications, the challenges it faces, and the possible ethical implications of the technology. Artificial Intelligence and Crime Prediction: The Basics CrimeGPT uses machine learning algorithms to analyze large data sets, identifying patterns that can predict where and when crimes are likely to occur. These data sets include historical crime statistics, demographic information, economic indicators, weather patterns, and more. By identifying trends that human analysts might miss, artificial intelligence can empower law enforcement agencies
 Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
01 Outlook Summary Currently, it is difficult to achieve an appropriate balance between detection efficiency and detection results. We have developed an enhanced YOLOv5 algorithm for target detection in high-resolution optical remote sensing images, using multi-layer feature pyramids, multi-detection head strategies and hybrid attention modules to improve the effect of the target detection network in optical remote sensing images. According to the SIMD data set, the mAP of the new algorithm is 2.2% better than YOLOv5 and 8.48% better than YOLOX, achieving a better balance between detection results and speed. 02 Background & Motivation With the rapid development of remote sensing technology, high-resolution optical remote sensing images have been used to describe many objects on the earth’s surface, including aircraft, cars, buildings, etc. Object detection in the interpretation of remote sensing images
 Recommendation system for NetEase Cloud Music cold start technology
Nov 14, 2023 am 08:14 AM
Recommendation system for NetEase Cloud Music cold start technology
Nov 14, 2023 am 08:14 AM
1. Problem background: The necessity and importance of cold start modeling. As a content platform, Cloud Music has a large amount of new content online every day. Although the amount of new content on the cloud music platform is relatively small compared to other platforms such as short videos, the actual amount may far exceed everyone's imagination. At the same time, music content is significantly different from short videos, news, and product recommendations. The life cycle of music spans extremely long periods of time, often measured in years. Some songs may explode after being dormant for months or years, and classic songs may still have strong vitality even after more than ten years. Therefore, for the recommendation system of music platforms, it is more important to discover unpopular and long-tail high-quality content and recommend them to the right users than to recommend other categories.
 Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
1. Background of the Construction of 58 Portraits Platform First of all, I would like to share with you the background of the construction of the 58 Portrait Platform. 1. The traditional thinking of the traditional profiling platform is no longer enough. Building a user profiling platform relies on data warehouse modeling capabilities to integrate data from multiple business lines to build accurate user portraits; it also requires data mining to understand user behavior, interests and needs, and provide algorithms. side capabilities; finally, it also needs to have data platform capabilities to efficiently store, query and share user profile data and provide profile services. The main difference between a self-built business profiling platform and a middle-office profiling platform is that the self-built profiling platform serves a single business line and can be customized on demand; the mid-office platform serves multiple business lines, has complex modeling, and provides more general capabilities. 2.58 User portraits of the background of Zhongtai portrait construction
 Add SOTA in real time and skyrocket! FastOcc: Faster inference and deployment-friendly Occ algorithm is here!
Mar 14, 2024 pm 11:50 PM
Add SOTA in real time and skyrocket! FastOcc: Faster inference and deployment-friendly Occ algorithm is here!
Mar 14, 2024 pm 11:50 PM
Written above & The author’s personal understanding is that in the autonomous driving system, the perception task is a crucial component of the entire autonomous driving system. The main goal of the perception task is to enable autonomous vehicles to understand and perceive surrounding environmental elements, such as vehicles driving on the road, pedestrians on the roadside, obstacles encountered during driving, traffic signs on the road, etc., thereby helping downstream modules Make correct and reasonable decisions and actions. A vehicle with self-driving capabilities is usually equipped with different types of information collection sensors, such as surround-view camera sensors, lidar sensors, millimeter-wave radar sensors, etc., to ensure that the self-driving vehicle can accurately perceive and understand surrounding environment elements. , enabling autonomous vehicles to make correct decisions during autonomous driving. Head



