Use Python to implement RSA encryption and decryption
I saw an English article [1] yesterday, showing how to use Python to implement the RSA algorithm. The logic of the code is the same as the previous article Understanding the RSA Algorithm. Friends who are not familiar with RSA can read the article Understanding the RSA Algorithm. , which explains what RSA is, the mathematical principles of RSA, and gives a simple example. It can be said to be the easiest article to understand RSA on Quanzhihu (this comes from a reader's comment).
I ran the code provided in English and found that it could not encrypt Chinese, so I modified the encryption and decryption functions to support Chinese encryption and decryption. Today’s article will share how to use Python to implement the RSA encryption and decryption process to help you establish an intuitive understanding of RSA. The random prime number generation algorithm in the code is also worth learning.
0. Effect demonstration
Let’s take a look at the effect first.
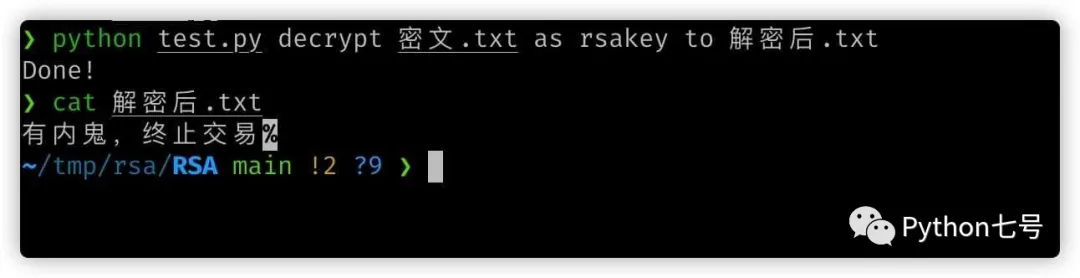
Original text: "There is a mole, terminate the transaction"

The cipher text cannot be cracked at all:

After decryption:
The complete code public account "Python No. 7" can be obtained by replying "rsa".
1. Key pair generation
Ideas:
1) Randomly find two prime numbers (prime numbers) p and q. The larger p and q, the safer they are. Here we choose a 1024-bit prime number:
p = genprime(1024) q = genprime(1024)
genprime() Let’s not talk about the implementation process of the function.
2) Calculate their product n = p * q and Euler function lambda_n.
n = p * q lambda_n = (p - 1) * (q - 1)
3) Randomly select an integer e, the condition is 1 < e < lambda_n, and e and lambda_n are relatively prime. For example, if you select 35537, 35537 has only 16 bits and must be smaller than lambda_n. < e < lambda_n,且 e 与 lambda_n 互质。比如选择 35537,35537 只有 16 位,必然小于 lambda_n。
e = 35537
4) Find an integer d such that the remainder of e * d divided by lambda_n is 1, and return the key pair.
d = eucalg(e, lambda_n)[0] if d < 0: d += lambda_n return (d, n), (e, n)
The implementation of the eucalg function will be discussed later.
At this point, the key pair generation function is as follows:
def create_keys(): p = genprime(1024) q = genprime(1024) n = p * q lambda_n = (p - 1) * (q - 1) e = 35537 d = eucalg(e, lambda_n)[0] if d < 0: d += lambda_n return (d, n), (e, n)
2. Implementation of encryption and decryption
The encryption and decryption processes are the same, public key encryption, private key encryption Key decryption, and vice versa, private key encryption and public key decryption, but the former is called encryption and the latter is called signature.
The specific function implementation is as follows:
def encrypt_data(data,key): e_data = [] for d in data: e = modpow(d, key[0], key[1]) e_data.append(e) return e_data ## 加密和解密的逻辑完全一样 decrypt_data = encrypt_data
The modpow function is used here, which is used to calculate the formula b^e % n = r.
- If it is an encryption process, then b is the plaintext, (n,e) is the public key, and r is the ciphertext.
- If it is a decryption process, then b is the ciphertext, (n, d) is the private key, and r is the famous text.
modpow is defined as follows:
def modpow(b, e, n): # find length of e in bits tst = 1 siz = 0 while e >= tst: tst <<= 1 siz += 1 siz -= 1 # calculate the result r = 1 for i in range(siz, -1, -1): r = (r * r) % n if (e >> i) & 1: r = (r * b) % n return r
3. Generating function of random prime numbers
Generating function of random prime numbers, which uses matrix multiplication and Fibonacci Sequence shows the importance of mathematics to algorithms.
# matrix multiplication def sqmatrixmul(m1, m2, w, mod): mr = [[0 for j in range(w)] for i in range(w)] for i in range(w): for j in range(w): for k in range(w): mr[i][j] = (mr[i][j] + m1[i][k] * m2[k][j]) % mod return mr # fibonacci calculator def fib(x, mod): if x < 3: return 1 x -= 2 # find length of e in bits tst = 1 siz = 0 while x >= tst: tst <<= 1 siz += 1 siz -= 1 # calculate the matrix fm = [ # function matrix [0, 1], [1, 1] ] rm = [ # result matrix # (identity) [1, 0], [0, 1] ] for i in range(siz, -1, -1): rm = sqmatrixmul(rm, rm, 2, mod) if (x >> i) & 1: rm = sqmatrixmul(rm, fm, 2, mod) # second row of resulting vector is result return (rm[1][0] + rm[1][1]) % mod def genprime(siz): while True: num = (1 << (siz - 1)) + secrets.randbits(siz - 1) - 10; # num must be 3 or 7 (mod 10) num -= num % 10 num += 3 # 3 (mod 10) # heuristic test if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0: return num num += 5 # 7 (mod 10) # heuristic test if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0: return num
4. Implementation of eucalg function
The essence of the function is to find the solution to the following linear equation of two variables:
e * x - lambda_n * y =1
Specific code:
def eucalg(a, b): # make a the bigger one and b the lesser one swapped = False if a < b: a, b = b, a swapped = True # ca and cb store current a and b in form of # coefficients with initial a and b # a' = ca[0] * a + ca[1] * b # b' = cb[0] * a + cb[1] * b ca = (1, 0) cb = (0, 1) while b != 0: # k denotes how many times number b # can be substracted from a k = a // b # swap a and b so b is always the lesser one a, b, ca, cb = b, a-b*k, cb, (ca[0]-k*cb[0], ca[1]-k*cb[1]) if swapped: return (ca[1], ca[0]) else: return ca
5 , test
test.py script usage method:
1), generate key
python test.py make-keys rsakey
The public key is saved in rsakey.pub, and the private key is saved in rsakey.priv中
2), Encrypt the file content
If there is a plain text .txt file:
python test.py encrypt 明文.txt from rsakey to 密文.txt
will generate a ciphertext .txt
3. Encrypt the file Content decryption
If there is a file ciphertext.txt:
python test.py decrypt 密文.txt as rsakey to 解密后.txt
will generate a decrypted .txt
Final words
This article shares the Python of the RSA algorithm A simple implementation can help understand the RSA algorithm.
The above is the detailed content of Use Python to implement RSA encryption and decryption. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
 The 2-Hour Python Plan: A Realistic Approach
Apr 11, 2025 am 12:04 AM
The 2-Hour Python Plan: A Realistic Approach
Apr 11, 2025 am 12:04 AM
You can learn basic programming concepts and skills of Python within 2 hours. 1. Learn variables and data types, 2. Master control flow (conditional statements and loops), 3. Understand the definition and use of functions, 4. Quickly get started with Python programming through simple examples and code snippets.
 How to read redis queue
Apr 10, 2025 pm 10:12 PM
How to read redis queue
Apr 10, 2025 pm 10:12 PM
To read a queue from Redis, you need to get the queue name, read the elements using the LPOP command, and process the empty queue. The specific steps are as follows: Get the queue name: name it with the prefix of "queue:" such as "queue:my-queue". Use the LPOP command: Eject the element from the head of the queue and return its value, such as LPOP queue:my-queue. Processing empty queues: If the queue is empty, LPOP returns nil, and you can check whether the queue exists before reading the element.
 How to start the server with redis
Apr 10, 2025 pm 08:12 PM
How to start the server with redis
Apr 10, 2025 pm 08:12 PM
The steps to start a Redis server include: Install Redis according to the operating system. Start the Redis service via redis-server (Linux/macOS) or redis-server.exe (Windows). Use the redis-cli ping (Linux/macOS) or redis-cli.exe ping (Windows) command to check the service status. Use a Redis client, such as redis-cli, Python, or Node.js, to access the server.
 How to read data from redis
Apr 10, 2025 pm 07:30 PM
How to read data from redis
Apr 10, 2025 pm 07:30 PM
To read data from Redis, you can follow these steps: 1. Connect to the Redis server; 2. Use get(key) to get the value of the key; 3. If you need string values, decode the binary value; 4. Use exists(key) to check whether the key exists; 5. Use mget(keys) to get multiple values; 6. Use type(key) to get the data type; 7. Redis has other read commands, such as: getting all keys in a matching pattern, using cursors to iterate the keys, and sorting the key values.
 Python vs. C : Applications and Use Cases Compared
Apr 12, 2025 am 12:01 AM
Python vs. C : Applications and Use Cases Compared
Apr 12, 2025 am 12:01 AM
Python is suitable for data science, web development and automation tasks, while C is suitable for system programming, game development and embedded systems. Python is known for its simplicity and powerful ecosystem, while C is known for its high performance and underlying control capabilities.
 What types of files are composed of oracle databases?
Apr 11, 2025 pm 03:03 PM
What types of files are composed of oracle databases?
Apr 11, 2025 pm 03:03 PM
Oracle database file structure includes: data file: storing actual data. Control file: Record database structure information. Redo log files: record transaction operations to ensure data consistency. Parameter file: Contains database running parameters to optimize performance. Archive log file: Backup redo log file for disaster recovery.
 How to find keys with redis
Apr 10, 2025 pm 05:45 PM
How to find keys with redis
Apr 10, 2025 pm 05:45 PM
There are several ways to find keys in Redis: Use the SCAN command to iterate over all keys by pattern or condition. Use GUI tools such as Redis Explorer to visualize the database and filter keys by name or schema. Write external scripts to query keys using the Redis client library. Subscribe to keyspace notifications to receive alerts when key changes.
 How to obtain redis login permission
Apr 10, 2025 pm 07:18 PM
How to obtain redis login permission
Apr 10, 2025 pm 07:18 PM
To obtain Redis login permission, you need to perform the following steps: 1. Create a username and password; 2. Allow remote connections; 3. Restart the Redis server; 4. Connect using the Redis CLI or programming language.




