 Technology peripherals
Technology peripherals
 AI
AI
 Introduced for the first time! Using causal inference to do partially observable reinforcement learning
Introduced for the first time! Using causal inference to do partially observable reinforcement learning
Introduced for the first time! Using causal inference to do partially observable reinforcement learning
This article "Fast Counterfactual Inference for History-Based Reinforcement Learning" proposes a fast causal inference algorithm that greatly reduces the computational complexity of causal inference - to a level that can be combined with online reinforcement learning.
The theoretical contribution of this article mainly has two points:
1. Proposed the concept of time-averaged causal effect;
2. Extend the famous backdoor criterion from univariate intervention effect estimation to multivariate intervention effect estimation, which is called the step backdoor criterion.
Background
Requires basic knowledge about partially observable reinforcement learning and causal inference. I won’t introduce too much here, just give me a few portals:
Partially Observable Reinforcement Learning:
POMDP explanation https:// www.zhihu.com/zvideo/1326278888684187648
Causal reasoning:
Causal reasoning in deep neural networks https://zhuanlan.zhihu .com/p/425331915
Motivation
Extracting/encoding features from historical information is a basic means to solve partially observable reinforcement learning. The mainstream method is to use the sequence-to-sequence (seq2seq) model to encode history. For example, the LSTM/GRU/NTM/Transformer reinforcement learning methods popular in the field fall into this category. What this type of method has in common is that history is encoded based on the correlation between historical information and learning signals (environmental rewards), that is, the greater the correlation of a piece of historical information, the higher the weight assigned to it. .
However, these methodscannot eliminate confounding correlations caused by sampling. Give an example of picking up a key to open the door, as shown in the figure below:
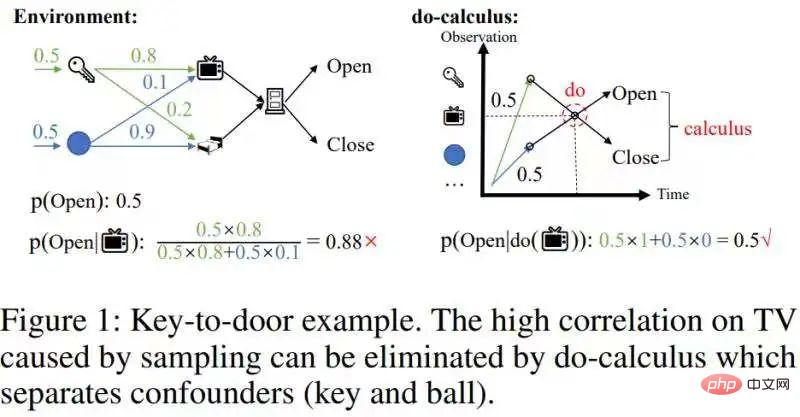
remove this confounding correlation.
This confounding correlation can be removed through do-calculus in causal inference [1]:Separate Potentially confusing Backdoor variablesKey and ball, thus cutting off the statistical correlation between the backdoor variable (key/ball) and the TV, and then converting the conditional probability of p(Open|, key/ball) with respect to the backdoor variable (key/ball) Ball)Integrate (right picture of Figure 1), and get the real effect p(Open|do( ))=0.5. Since historical states with causal effects are relatively sparse, when we remove confounding correlations, the scale of historical states can be greatly reduced.
Therefore, we hope to use causal inference to remove confounding correlations in historical samples, and then use seq2seq to encode the history to obtain a more compact historical representation.(Motivation for this article)
[1] Note: What is considered here is do-calculus adjusted using the backdoor, with a popular science link https://blog.csdn .net/qq_31063727/article/details/118672598Performing causal inference in historical sequences is different from general causal inference problems. The variables in the historical sequence have both time and space dimensions , that is, observation-time combination Previous causal inference methods were based on univariate intervention detection and could only do one variable at a time. Performing causal reasoning on a large-scale historical state will result in extremely high time complexity, making it difficult to combine with online RL algorithms. [2] Note: The formal definition of the causal effect of univariate intervention is as follows As shown in the figure above Indicates that given the history , it is necessary to estimate the causal effect of on the transferred variable , do the following two steps: 1) Intervene in the historical state do , 2) Use the previous historical state as the backdoor variable, is the response variable. Calculate the following integral to obtain the required causal effect Since single variable intervention It is difficult to combine detection with online RL, so it is necessary to develop multivariate intervention detection methods. The core observation (hypothesis) of this article is that causal states are sparse in the spatial dimension. This observation is natural and common. For example, when you open a door with a key, many states will be observed during the process, but the observation value of the key determines whether the door can be opened. This observation value accounts for a sparse proportion of all observed values. Taking advantage of this sparsity, we can filter out a large number of historical states without causal effects at once through multi-variable intervention. But the causal effect is not sparse in the time dimension. It is also a key to open the door, and the key can be observed by the agent at most of the time. The density of causal effects in the time dimension prevents us from conducting multivariate interventions—it is impossible to remove a large number of historical states without causal effects at once. Based on the above two observations, our core idea is to first make inferences in the spatial dimension, and then make inferences in the time dimension. Use the sparsity in the spatial dimension to significantly reduce the number of interventions. In order to separately estimate the spatial causal effect, we propose to first obtain the time average causal effect, which means averaging the causal effects of multiple historical states over time (see the original text for specific definitions). Based on this idea, we focus on the problem: the core problem to be solved is how to calculateintervening in multiple different time stepsvariables with the same value (note The joint causal effect We improve the backdoor criterion and propose a criterion suitable for estimating multivariate joint intervention effect estimates. For any two intervened variables Step-backdoor adjustment formula ##This criterion separates other variables between the variables of two adjacent time steps, which are called step backdoor variables. In a causal diagram that satisfies this criterion, we can estimate the joint causal effect of any two intervening variables. It includes two steps: step 1. Use variables smaller than i at the time step as backdoor variables to estimate do The above formula uses the more general variable indicator X . For the case of more than three variables, by continuously using the step backdoor criterion - the variables between the adjacent intervening variables at each two time steps are regarded as step backdoor variables , continuously calculating the above formula, the joint causal effect of multi-variable intervention
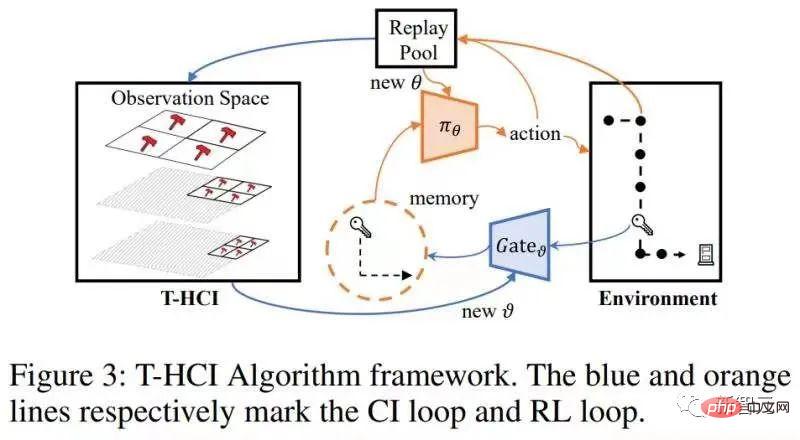
Specific to the partially observable reinforcement learning problem, after replacing x in the above formula with observation o, there is the following causal effect calculation formula: Theorem 2. Given ##At this point, the paper gives a formula for calculating spatial causal effects (i.e., time-averaged causal effects). This method reduces the number of interventions from O( The algorithm structure diagram is as follows The algorithm contains two loops, one It is a T-HCI loop, and the other is a policy learning loop. The two are exchanged: in the policy learning loop, the agent is sampled to learn a certain number of rounds, and the samples are stored in the replay pool; in the T-HCI loop, the stored samples are used Carry out the causal inference process described above. Limitations: Causal inference in the spatial dimension has already compressed the historical scale sufficiently. Although causal inference in the time dimension can further compress the historical scale, considering that the computational complexity needs to be balanced, this article retains correlation inference in the time dimension (using LSTM end-to-end on historical states with spatial causal effects) and does not use Causal reasoning. Experimentally verified three points, responding to the previous claims: 1) Can T-HCI improve the sample efficiency of RL methods? 2) Is the computational overhead of T-HCI acceptable in practice? 3) Can T-HCI mine observations with causal effects? Please see the experimental chapter of the paper for details, so I won’t take up space here. Of course, interested friends can also send me a private message/comment. Two points to start the discussion: 1. HCI is not limited to types of reinforcement learning. Although this article studies online RL, HCI can also be naturally extended to offline RL, model-based RL, etc., and you can even consider applying HCI to imitation learning; 2. HCI can be regarded as a special hard attention method-sequence points with causal effect receive an attention weight of 1, and otherwise receive an attention weight of 0. From this perspective, some sequence prediction problems may also try to be handled using HCI. Difficulty
 , where o is the observation and t is the timestamp (in contrast, MDP Very friendly, Markov state has only spatial dimension). The overlap of the two dimensions makes the scale of historical observations quite large -
, where o is the observation and t is the timestamp (in contrast, MDP Very friendly, Markov state has only spatial dimension). The overlap of the two dimensions makes the scale of historical observations quite large -  is used to represent the number of observation values at each timestamp, and T is used to represent the total length of time, then the historical state There are
is used to represent the number of observation values at each timestamp, and T is used to represent the total length of time, then the historical state There are  kinds of values (the regular form O( ) is the complexity symbol). [2]
kinds of values (the regular form O( ) is the complexity symbol). [2]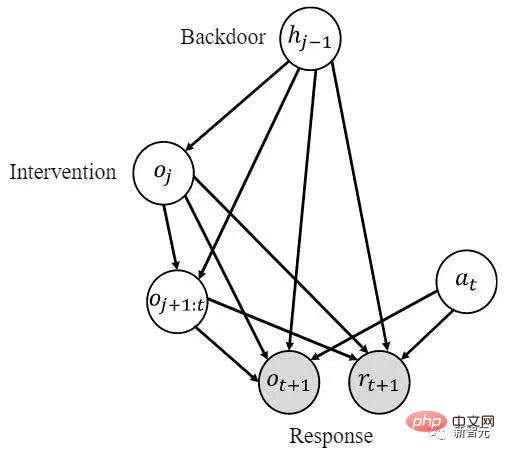

Ideas
 of ). This is because the backdoor criterion does not apply to joint intervention of multiple historical variables: as shown in the figure below, consider joint intervention of the double variables
of ). This is because the backdoor criterion does not apply to joint intervention of multiple historical variables: as shown in the figure below, consider joint intervention of the double variables 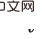 and
and  , you can see that part of the backdoor variables at the later time step of
, you can see that part of the backdoor variables at the later time step of  contains
contains  , and there is no common backdoor variable between the two.
, and there is no common backdoor variable between the two. 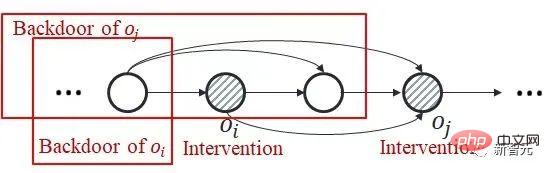
Method
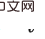 and
and 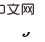 (i
(i
 causal effect; step 2. Take a determined
causal effect; step 2. Take a determined  The backdoor variable and the given
The backdoor variable and the given  are used as conditions, and the variables between
are used as conditions, and the variables between  and
and 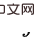 are New backdoor variables about
are New backdoor variables about 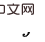 (that is, stepping backdoor variables about
(that is, stepping backdoor variables about  and
and  ), it is estimated that do
), it is estimated that do 'sConditional Causal Effect. Then the joint causal effect is the product integral of these two parts. The step-by-step backdoor criterion uses two steps of the ordinary backdoor criterion, as shown in the figure below
'sConditional Causal Effect. Then the joint causal effect is the product integral of these two parts. The step-by-step backdoor criterion uses two steps of the ordinary backdoor criterion, as shown in the figure below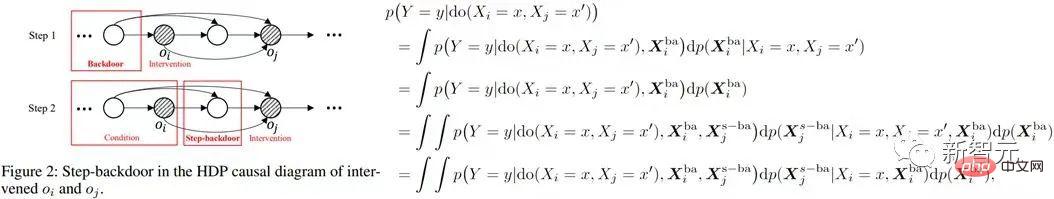
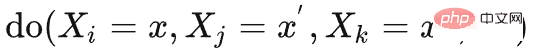 can be obtained as follows:
can be obtained as follows: 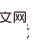 and
and 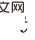 , the causal effect of Do(o) can be estimated by
, the causal effect of Do(o) can be estimated by
 ) to O(
) to O(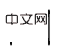 ). The next step is to take advantage of the sparsity of spatial causal effects (mentioned at the beginning of this chapter) to further reduce the number of interventions exponentially. Replace the intervention on one observation with the intervention on an observation subspace - this is a common idea to take advantage of sparsity to speed up calculations (see original article). In this article, a fast counterfactual inference algorithm called Tree-based history counterfactual inference (T-HCI) is developed, which will not be described in detail here (see the original text for details). In fact, many historical causal inference algorithms can be developed based on the stepping backdoor criterion, and T-HCI is just one of them. The final result is Proposition 3 (Coarse-to-fine CI). If
). The next step is to take advantage of the sparsity of spatial causal effects (mentioned at the beginning of this chapter) to further reduce the number of interventions exponentially. Replace the intervention on one observation with the intervention on an observation subspace - this is a common idea to take advantage of sparsity to speed up calculations (see original article). In this article, a fast counterfactual inference algorithm called Tree-based history counterfactual inference (T-HCI) is developed, which will not be described in detail here (see the original text for details). In fact, many historical causal inference algorithms can be developed based on the stepping backdoor criterion, and T-HCI is just one of them. The final result is Proposition 3 (Coarse-to-fine CI). If , the number of interventions for coarse-to-fine CI is
, the number of interventions for coarse-to-fine CI is ).
). 
The above is the detailed content of Introduced for the first time! Using causal inference to do partially observable reinforcement learning. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 How to use char array in C language
Apr 03, 2025 pm 03:24 PM
How to use char array in C language
Apr 03, 2025 pm 03:24 PM
The char array stores character sequences in C language and is declared as char array_name[size]. The access element is passed through the subscript operator, and the element ends with the null terminator '\0', which represents the end point of the string. The C language provides a variety of string manipulation functions, such as strlen(), strcpy(), strcat() and strcmp().
 Avoid errors caused by default in C switch statements
Apr 03, 2025 pm 03:45 PM
Avoid errors caused by default in C switch statements
Apr 03, 2025 pm 03:45 PM
A strategy to avoid errors caused by default in C switch statements: use enums instead of constants, limiting the value of the case statement to a valid member of the enum. Use fallthrough in the last case statement to let the program continue to execute the following code. For switch statements without fallthrough, always add a default statement for error handling or provide default behavior.
 The importance of default in switch case statement (C language)
Apr 03, 2025 pm 03:57 PM
The importance of default in switch case statement (C language)
Apr 03, 2025 pm 03:57 PM
The default statement is crucial in the switch case statement because it provides a default processing path that ensures that a block of code is executed when the variable value does not match any case statement. This prevents unexpected behavior or errors and enhances the robustness of the code.
 What are the types of return values of c language function? Summary of types of return values of c language function?
Apr 03, 2025 pm 11:18 PM
What are the types of return values of c language function? Summary of types of return values of c language function?
Apr 03, 2025 pm 11:18 PM
The return value types of C language function include int, float, double, char, void and pointer types. int is used to return integers, float and double are used to return floats, and char returns characters. void means that the function does not return any value. The pointer type returns the memory address, be careful to avoid memory leakage.结构体或联合体可返回多个相关数据。
 What is the value range of char in C language
Apr 03, 2025 pm 03:39 PM
What is the value range of char in C language
Apr 03, 2025 pm 03:39 PM
The value range of char in C language depends on the implementation method: signed char: -128 to 127 Unsigned char: 0 to 255 The specific range is affected by computer architecture and compiler options. By default, char is set to a signed type.
 Concept of c language function
Apr 03, 2025 pm 10:09 PM
Concept of c language function
Apr 03, 2025 pm 10:09 PM
C language functions are reusable code blocks. They receive input, perform operations, and return results, which modularly improves reusability and reduces complexity. The internal mechanism of the function includes parameter passing, function execution, and return values. The entire process involves optimization such as function inline. A good function is written following the principle of single responsibility, small number of parameters, naming specifications, and error handling. Pointers combined with functions can achieve more powerful functions, such as modifying external variable values. Function pointers pass functions as parameters or store addresses, and are used to implement dynamic calls to functions. Understanding function features and techniques is the key to writing efficient, maintainable, and easy to understand C programs.
 C# multi-threaded method to prevent jamming
Apr 03, 2025 pm 02:54 PM
C# multi-threaded method to prevent jamming
Apr 03, 2025 pm 02:54 PM
The following ways to avoid "stuck" multithreading in C#: avoid time-consuming operations on UI threads. Use Task and async/await to perform time-consuming operations asynchronously. Update the UI on the UI thread via Application.Current.Dispatcher.Invoke. Use the CancellationToken to control task cancellation. Make rational use of thread pools to avoid excessive creation of threads. Pay attention to code readability and maintainability, making it easy to debug. Logs are recorded in each thread for easy debugging.
 C Programmer &#s Undefined Behavior Guide
Apr 03, 2025 pm 07:57 PM
C Programmer &#s Undefined Behavior Guide
Apr 03, 2025 pm 07:57 PM
Exploring Undefined Behaviors in C Programming: A Detailed Guide This article introduces an e-book on Undefined Behaviors in C Programming, a total of 12 chapters covering some of the most difficult and lesser-known aspects of C Programming. This book is not an introductory textbook for C language, but is aimed at readers familiar with C language programming, and explores in-depth various situations and potential consequences of undefined behaviors. Author DmitrySviridkin, editor Andrey Karpov. After six months of careful preparation, this e-book finally met with readers. Printed versions will also be launched in the future. This book was originally planned to include 11 chapters, but during the creation process, the content was continuously enriched and finally expanded to 12 chapters - this itself is a classic array out-of-bounds case, and it can be said to be every C programmer





