
In October 1950, a paper titled "Can Machines Think" was published. This paper proposes a horrifying test, in which the tester is separated from the person being tested (a real person and a machine) by randomly asking questions to the person being tested through a communication device, and asking them to Testers guessed whether the person they were talking to was a real person or a machine.
After multiple tests, if the machine can make each participant make more than 30% misjudgments on average, then the machine has passed the test and is considered to have human capabilities. intelligent.
This is when people first realized that robots might possess human intelligence. This test is the Turing test that millions of science fiction enthusiasts talk about. This article also won the author Alan Turing the title of "Father of Artificial Intelligence".
The road to artificial intelligence, or the origin of the history of computer development, is a paper published by Turing when he was 24 years old. In this paper, he gave a strict mathematical definition to "computability" and proposed the idea of the famous "Turing Machine". The Turing machine is not a specific machine, but a mental model that can create a very simple but extremely powerful computing device that can be used to calculate all imaginable computable functions.
Because Turing invented the Turing machine, from time to time someone jumps out and claims that Turing actually "invented the computer." However, Turing machines are not designed in the same way as actual computing machines. A Turing machine is not even an abstract model of a machine. It turns out (as evidenced by Turing's remarks) that a Turing machine is a model of a person writing on paper on a table. So, why did Turing invent the Turing machine, and where will the Turing machine lead us?
The best way to answer these questions is to put the textbook aside and open it paper. Today, borrowing a 1936 journal doesn’t require filling out a loan card or waiting an hour for a librarian to fetch it from the library. All we need is a glass of malt whiskey in hand and easy access to Google at home. The Turing paper we are looking for is as follows:

Paper address: https://www.cs.virginia.edu/ ~robins/Turing_Paper_1936.pdf
There are some errors in the paper, but the flaws do not outweigh the flaws. As Joel David Hamkins said, Turing defined computable real numbers as numbers with computable decimal expansions, which actually doesn't work, but it's not difficult to correct.
Turing explained the intention of writing this paper in the title: "On Computable Numbers and Their Application in "Decision Problems"". Among them, "Entscheidungsproblem (Decision Problem)" )" asks whether there is an efficient technique for deciding that a given first-order logic formula is valid, that is, true on all interpretations.
Turing developed his idea as follows:
We can compare a person who is calculating real numbers to a machine that can only satisfy a limited number of conditions q1, q2,... qR.... There is one in this machine A long "paper tape" passes through it, and the paper tape is divided into many parts. We call these pieces squares, and each square can carry a "symbol"... some write down The symbols form the decimal digit sequence of the real numbers being calculated, while the other symbols are just rough notes to "aid in memory". These rough notes can be erased. My argument is that this slippage on the tape The operation method of swiping back and forth to a certain symbol and processing the symbol accordingly, including all operations used for numerical calculations.
……
"Computable numbers" simply means real numbers whose decimal expression can be calculated using limited means. According to my definition, if the decimal expression of a number can be written down by a machine, then this Numbers are computable.
Turing subsequently defined and proved it. This is a typical mathematics paper, not a typical engineering paper. In this kind of article, readers want to See the discussion on how to implement a certain mechanism described in the article. From Turing's title and article we can see that Turing's main concern is the calculation of a real number to infinite decimal places.
This paper has many other important contributions:
After writing this paper, Turing opened up the theoretical computing science The gate to the field.
We are not sure what gave Turing the idea of a Universal Turing Machine (UTM), but once he Come to think of it, he might think that the existence of a universal Turing machine is obvious. Since the purpose of a Turing machine is to simulate a clerk working at a desk, and the operation of a Turing machine is the same as that of a clerk—performing this or that operation according to a given list of transformation rules based on the machine state and tape symbols—it is obviously necessary A Turing machine to perform such routine tasks. Turing's paper was a little sketchy on the details of the construction, but no one seemed to mind.
Now, we have a universal Turing machine that has been designed incisively and vividly. Decades ago, at the University of Cambridge, Dr. Ken Moody wrote a universal Minsky keygen:

Link: http: //www.igblan.free-online.co.uk/igblan/ca/minsky.html
Such a machine has limited registers, each register can store any Large nonnegative integer. It has a finite program consisting of three different types of label instructions:
Such machines are easier to program than Turing machines, although they still don't look like real computers.
Moody uses a standard bijection between N and N×N to pack a list of integers into a single integer. He wrote a small library of small register machines that performed operations such as pushing up and popping off the stack, and created a design that was reminiscent of the fetch-execution cycle of a real processor. The entire process can be seen in the following slides. The picture below is the machine itself:
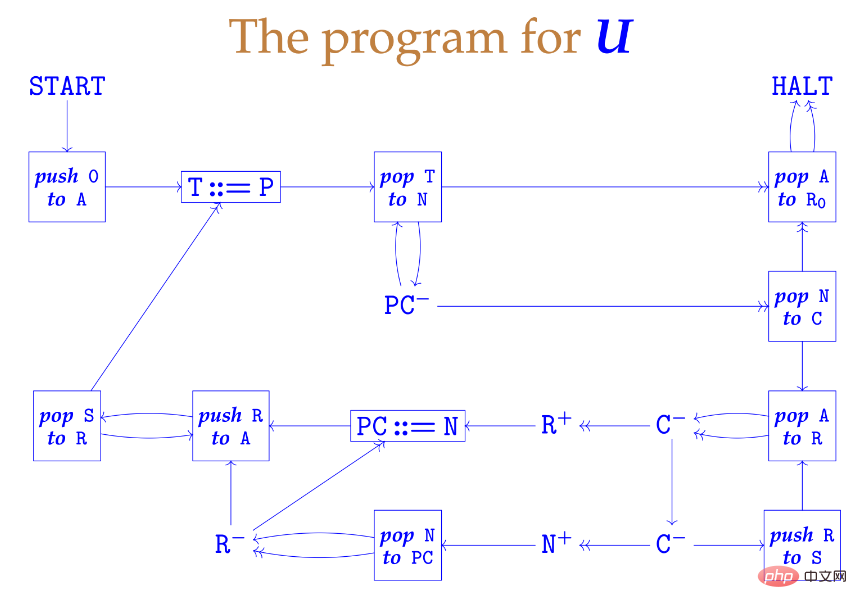
The picture below is the overall structure of the machine. (The authors of these two pictures are Andrew Pitts, professor of theoretical computing science at the University of Cambridge.)

Surprisingly, the structure of this machine is so simple !
The halt problem is obviously undecidable. Otherwise, many mathematical conjectures will be difficult to solve, such as Fermat's Last Theorem: Just write a program that searches for x, y, z, n>2, make 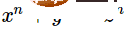 , and ask if it terminates. However, the undecidability of halting must be rigorously expressed and proven.
, and ask if it terminates. However, the undecidability of halting must be rigorously expressed and proven.
Contrary to popular belief, Turing's paper did not discuss the halting problem, but discussed a characteristic related to the halting problem, which he called "circularity". A Turing machine is cyclic if it "writes only a limited number of the first symbols" (i.e. 0s and 1s). I think the reason why cyclicity is important is that Turing was particularly fond of approximating real numbers as infinite binary strings. Physicist Christopher Strachey claimed in a 1965 letter to Computer Journal that Turing told him a proof of the undecidability of the halting problem.
In September 2009, David P. Anderson interviewed Maurice Wilkes, and his view of Turing was exactly the opposite of the public:
David P. Anderson: What do you think is the importance of Turing’s 1936 paper on the decision problem?
Maurice Wilkes: I think an engineer would look at the idea of stored programs as a sort of holy trinity and say, "This is absolutely first-rate. This is how it should be done."
There is no practical difference between the ideas in that paper and what I said. He was lucky to get that paper published, I mean Alonzo Church got the same result using other methods.
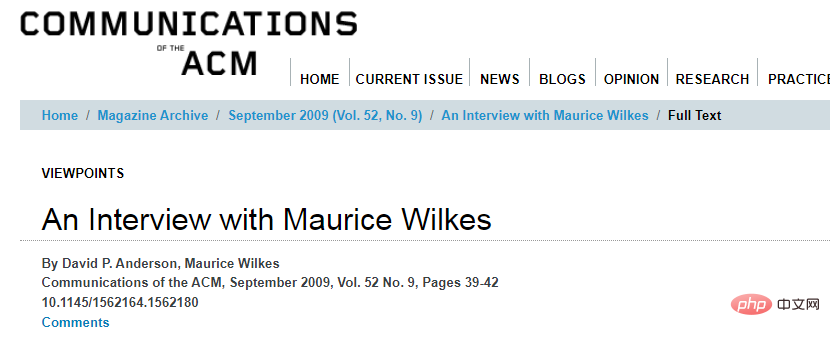
Article address: https://cacm.acm.org/magazines/2009/9/38898-an-interview-with -maurice-wilkes/fulltext
##It should be noted that at the time of the interview, Maurice Wilkes was 96 years old. He himself is a famous computer pioneer, EDSAC (Electronic Father of the Delay Storage Automatic Calculator, the electronic delay storage automatic calculator. In his strange answer, one can see his jealousy of Turing's lofty status. These two obviously don't get along! We also see Maurice Wilkes's disdain for theory: although encoding the machine into numbers was expected of a stored-program computer, Turing's work was pure mathematics and had no engineering significance. Turing was interested in actual computer engineering, but his many attempts to participate in real projects were frustrated.
And how do you evaluate those remarks about Church?
While Turing was doing research, many researchers focused on the idea of "effective computability." Here I recommend readers to read "An Unsolvable Problem in Elementary Number Theory" by Qiu Qi (see the picture below).

Paper link: https://www.jstor.org/stable/2371045?origin=crossref
To be honest, this paper is difficult to read, but it can take us into the scene. This article gives a definition of λ-calculus, a definition of a recursive function (in the Kleene/Gödel sense), and some indisputable questions about the existence and equivalence of paradigms in λ-calculus. judgement result. Church and Craney had proved the equivalence between lambda-definable functions and recursive functions; and while Turing was at Princeton, the equivalence between lambda-definable functions and Turing-computable functions had also been proven , so we get the Church-Turing thesis, which refers to the fact that effectively computable functions are precisely those functions in the mathematical equivalence class.
As is often said, we cannot prove whether this thesis is correct or not, because "effectively computable" is not a precise concept. We can think of Turing computable functions as a rather inclusive class, because it includes many functions that cannot be calculated within the lifetime of the universe. With the help of Ackermann function, we can easily get the example.
The modern form of the Ackermann function is as follows:
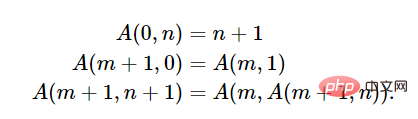
Article link: https:// lawrencecpaulson.github.io/2022/02/09/Ackermann-example.html
If you define f(n)=A(n,n), you cannot expect Calculate the even number f(4). g(n)=A(4,n), although primitive recursion, is almost impossible to compute.
Although there were no digital computers until the 1930s, the concept of efficient computability was well known to mathematicians. The concept of validity has long appeared in the straight line structure and compass structure of Greek geometry. Validity is also an integral part of the decision problem and Hilbert's tenth problem. The genius of Turing's concept, compared to Gödel's recursive functions and Church's lambda calculus, is that it is obviously correct. Gödel himself was not sure whether his recursive function captured the idea of calculation, and we don't know whether Church's idea was correct. Only Turing's ideas were simple and natural. Turing's ideas are provably equivalent to other models and provide reasonable explanations for all of them. He pointed out this fact in his 1937 paper "Computability and Lambda-Definability".
This article aims to prove that the computable function proposed by the author is consistent with Qiu Qi’s λ-definable function and the one proposed by Elbrown and Brother The general recursive function proposed by Del and developed by Kleiny is the same. These same functions prove that every X-defined function is computable, and every computable function is generally recursive.
Note that Turing wrote "computable", but we have to write "Turing computable".
The above is the detailed content of Turing Machine: How can we talk about computing in the absence of computers?. For more information, please follow other related articles on the PHP Chinese website!
 teambition
teambition
 Usage of write function
Usage of write function
 What are the requirements for Douyin live broadcast?
What are the requirements for Douyin live broadcast?
 The difference between UCOS and linux
The difference between UCOS and linux
 What are the commonly used instructions in vue?
What are the commonly used instructions in vue?
 How to solve the problem that js code cannot run after formatting
How to solve the problem that js code cannot run after formatting
 How to jump with parameters in vue.js
How to jump with parameters in vue.js
 What does mobile phone hd mean?
What does mobile phone hd mean?




