Ten commonly used distance measurement methods in machine learning
Distance metric is the basis of supervised and unsupervised learning algorithms, including k-nearest neighbor, support vector machine and k-means clustering.
The choice of distance metric affects our machine learning results, so it is important to consider which metric is best suited for the problem. Therefore, we should be cautious when deciding which measurement method to use. But before we make a decision, we need to understand how distance measurement works and what measurements we can choose from.
This article will briefly introduce commonly used distance measurement methods, how they work, how to calculate them in Python, and when to use them. This deepens knowledge and understanding and improves machine learning algorithms and results.
Before we delve deeper into the different distance measurements, we first need to have a general idea of how they work and how to choose the appropriate measurement.
Distance metric is used to calculate the difference between two objects in a given problem space, i.e. features in the dataset. This distance can then be used to determine the similarity between features, with the smaller the distance, the more similar the features.
For distance measurement, we can choose between geometric distance measurement and statistical distance measurement. Which distance measurement should be chosen depends on the type of data. Features may be of different data types (e.g., real values, Boolean values, categorical values), and the data may be multidimensional or consist of geospatial data.
Geometric distance measurement
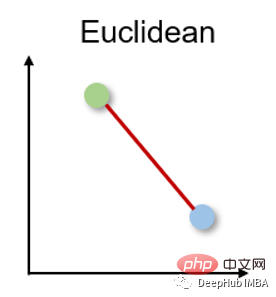
1. Euclidean distance Euclidean distance
Euclidean distance measures the shortest distance between two real-valued vectors. Due to its intuitiveness, simplicity of use and good results for many use cases, it is the most commonly used distance metric and the default distance metric for many applications.
Euclidean distance can also be called l2 norm, and its calculation method is:
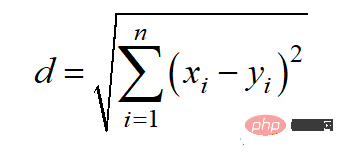
The Python code is as follows
from scipy.spatial import distance distance.euclidean(vector_1, vector_2)
Euclidean distance has two main disadvantages. First, distance measurements do not work with data of higher dimensions than 2D or 3D space. Second, if we do not normalize and/or normalize the features, distances may be skewed by units.
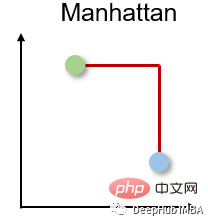
2. Manhattan distance
Manhattan distance is also called taxi or city block distance because the distance between two real-valued vectors is based on the fact that a person can only move at right angles computational. This distance measure is often used for discrete and binary attributes so that true paths can be obtained.
The Manhattan distance is based on the l1 norm, and the calculation formula is:
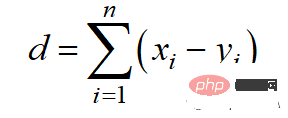
The Python code is as follows
from scipy.spatial import distance distance.cityblock(vector_1, vector_2)
The distance of Manhattan has two major disadvantages. It is not as intuitive as Euclidean distance in high-dimensional space, nor does it show the shortest possible path. While this may not be a problem, we should be aware that this is not the shortest distance.
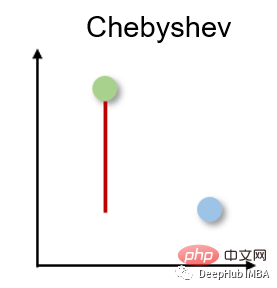
3. Chebyshev distance Chebyshev distance
The Chebyshev distance is also called the checkerboard distance because it is the maximum distance in any dimension between two real-valued vectors. It is commonly used in warehouse logistics, where the longest path determines the time required to get from one point to another.
The Chebyshev distance is calculated by l-infinite norm:
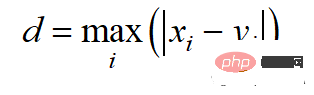
The Python code is as follows
from scipy.spatial import distance distance.chebyshev(vector_1, vector_2)
Chebyshev distance has only very specific use cases and is therefore rarely used.
4. Minkowski distance Minkowski distance
Minkowski distance is the generalized form of the above distance measure. It can be used for the same use cases while providing high flexibility. We can choose the p-value to find the most appropriate distance measure.
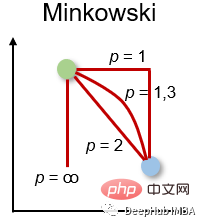
The calculation method of Minkowski distance is:
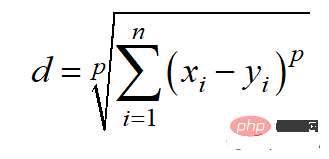
The Python code is as follows
from scipy.spatial import distance distance.minkowski(vector_1, vector_2, p)
Because Minkowski distance represents a different distance metric and has the same main drawbacks as them, such as problems in high-dimensional spaces and dependence on feature units. Additionally, the flexibility of p-values can also be a disadvantage, as it can reduce computational efficiency since multiple calculations are required to find the correct p-value.
5. Cosine similarity and distance Cosine similarity
Cosine similarity is a measure of direction. Its size is determined by the cosine between two vectors and ignores the size of the vector. Cosine similarity is often used in high dimensions where the size of the data does not matter, for example, recommender systems or text analysis.
余弦相似度可以介于-1(相反方向)和1(相同方向)之间,计算方法为:
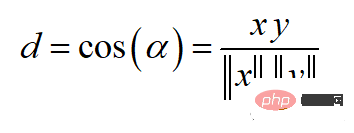
余弦相似度常用于范围在0到1之间的正空间中。余弦距离就是用1减去余弦相似度,位于0(相似值)和1(不同值)之间。
Python代码如下
from scipy.spatial import distance distance.cosine(vector_1, vector_2)
余弦距离的主要缺点是它不考虑大小而只考虑向量的方向。因此,没有充分考虑到值的差异。
6、半正矢距离 Haversine distance
半正矢距离测量的是球面上两点之间的最短距离。因此常用于导航,其中经度和纬度和曲率对计算都有影响。
半正矢距离的公式如下:
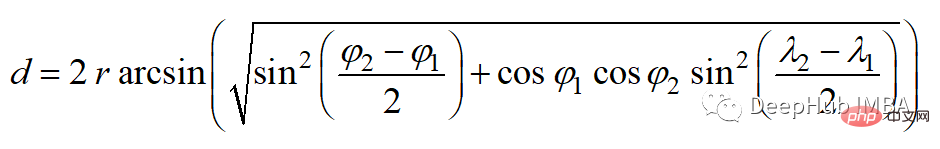
其中r为球面半径,φ和λ为经度和纬度。
Python代码如下
from sklearn.metrics.pairwise import haversine_distances haversine_distances([vector_1, vector_2])
半正矢距离的主要缺点是假设是一个球体,而这种情况很少出现。
7、汉明距离
汉明距离衡量两个二进制向量或字符串之间的差异。
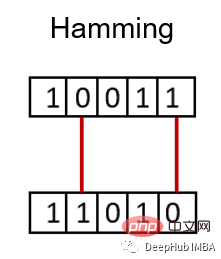
对向量按元素进行比较,并对差异的数量进行平均。如果两个向量相同,得到的距离是0之间,如果两个向量完全不同,得到的距离是1。
Python代码如下
from scipy.spatial import distance distance.hamming(vector_1, vector_2)
汉明距离有两个主要缺点。距离测量只能比较相同长度的向量,它不能给出差异的大小。所以当差异的大小很重要时,不建议使用汉明距离。
统计距离测量
统计距离测量可用于假设检验、拟合优度检验、分类任务或异常值检测。
8、杰卡德指数和距离 Jaccard Index
Jaccard指数用于确定两个样本集之间的相似性。它反映了与整个数据集相比存在多少一对一匹配。Jaccard指数通常用于二进制数据比如图像识别的深度学习模型的预测与标记数据进行比较,或者根据单词的重叠来比较文档中的文本模式。
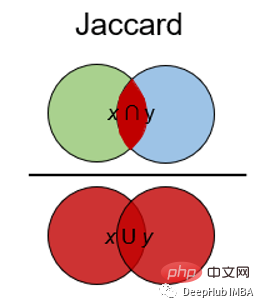
Jaccard距离的计算方法为:

Python代码如下
from scipy.spatial import distance distance.jaccard(vector_1, vector_2)
Jaccard指数和距离的主要缺点是,它受到数据规模的强烈影响,即每个项目的权重与数据集的规模成反比。
9、Sorensen-Dice指数
Sörensen-Dice指数类似于Jaccard指数,它可以衡量的是样本集的相似性和多样性。该指数更直观,因为它计算重叠的百分比。Sörensen-Dice索引常用于图像分割和文本相似度分析。
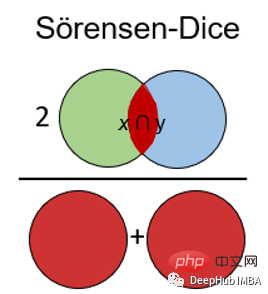
计算公式如下:
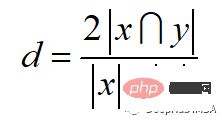
Python代码如下
from scipy.spatial import distance distance.dice(vector_1, vector_2)
它的主要缺点也是受数据集大小的影响很大。
10、动态时间规整 Dynamic Time Warping
动态时间规整是测量两个不同长度时间序列之间距离的一种重要方法。可以用于所有时间序列数据的用例,如语音识别或异常检测。
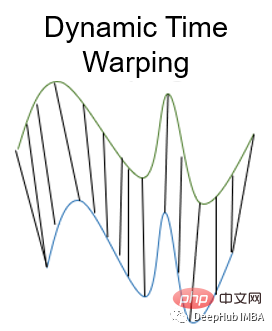
为什么我们需要一个为时间序列进行距离测量的度量呢?如果时间序列长度不同或失真,则上述面说到的其他距离测量无法确定良好的相似性。比如欧几里得距离计算每个时间步长的两个时间序列之间的距离。但是如果两个时间序列的形状相同但在时间上发生了偏移,那么尽管时间序列非常相似,但欧几里得距离会表现出很大的差异。
动态时间规整通过使用多对一或一对多映射来最小化两个时间序列之间的总距离来避免这个问题。当搜索最佳对齐时,这会产生更直观的相似性度量。通过动态规划找到一条弯曲的路径最小化距离,该路径必须满足以下条件:
- 边界条件:弯曲路径在两个时间序列的起始点和结束点开始和结束
- 单调性条件:保持点的时间顺序,避免时间倒流
- 连续条件:路径转换限制在相邻的时间点上,避免时间跳跃
- 整经窗口条件(可选):允许的点落入给定宽度的整经窗口
- 坡度条件(可选):限制弯曲路径坡度,避免极端运动
我们可以使用 Python 中的 fastdtw 包:
from scipy.spatial.distance import euclidean from fastdtw import fastdtw distance, path = fastdtw(timeseries_1, timeseries_2, dist=euclidean)
动态时间规整的一个主要缺点是与其他距离测量方法相比,它的计算工作量相对较高。
总结
在这篇文章中,简要介绍了十种常用的距离测量方法。本文中已经展示了它们是如何工作的,如何在Python中实现它们,以及经常使用它们解决什么问题。如果你认为我错过了一个重要的距离测量,请留言告诉我。
The above is the detailed content of Ten commonly used distance measurement methods in machine learning. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1385
1385
 52
52
 This article will take you to understand SHAP: model explanation for machine learning
Jun 01, 2024 am 10:58 AM
This article will take you to understand SHAP: model explanation for machine learning
Jun 01, 2024 am 10:58 AM
In the fields of machine learning and data science, model interpretability has always been a focus of researchers and practitioners. With the widespread application of complex models such as deep learning and ensemble methods, understanding the model's decision-making process has become particularly important. Explainable AI|XAI helps build trust and confidence in machine learning models by increasing the transparency of the model. Improving model transparency can be achieved through methods such as the widespread use of multiple complex models, as well as the decision-making processes used to explain the models. These methods include feature importance analysis, model prediction interval estimation, local interpretability algorithms, etc. Feature importance analysis can explain the decision-making process of a model by evaluating the degree of influence of the model on the input features. Model prediction interval estimate
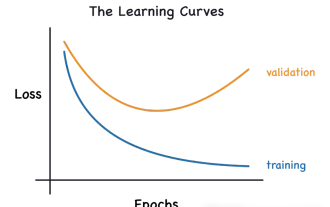 Identify overfitting and underfitting through learning curves
Apr 29, 2024 pm 06:50 PM
Identify overfitting and underfitting through learning curves
Apr 29, 2024 pm 06:50 PM
This article will introduce how to effectively identify overfitting and underfitting in machine learning models through learning curves. Underfitting and overfitting 1. Overfitting If a model is overtrained on the data so that it learns noise from it, then the model is said to be overfitting. An overfitted model learns every example so perfectly that it will misclassify an unseen/new example. For an overfitted model, we will get a perfect/near-perfect training set score and a terrible validation set/test score. Slightly modified: "Cause of overfitting: Use a complex model to solve a simple problem and extract noise from the data. Because a small data set as a training set may not represent the correct representation of all data." 2. Underfitting Heru
 Transparent! An in-depth analysis of the principles of major machine learning models!
Apr 12, 2024 pm 05:55 PM
Transparent! An in-depth analysis of the principles of major machine learning models!
Apr 12, 2024 pm 05:55 PM
In layman’s terms, a machine learning model is a mathematical function that maps input data to a predicted output. More specifically, a machine learning model is a mathematical function that adjusts model parameters by learning from training data to minimize the error between the predicted output and the true label. There are many models in machine learning, such as logistic regression models, decision tree models, support vector machine models, etc. Each model has its applicable data types and problem types. At the same time, there are many commonalities between different models, or there is a hidden path for model evolution. Taking the connectionist perceptron as an example, by increasing the number of hidden layers of the perceptron, we can transform it into a deep neural network. If a kernel function is added to the perceptron, it can be converted into an SVM. this one
 The evolution of artificial intelligence in space exploration and human settlement engineering
Apr 29, 2024 pm 03:25 PM
The evolution of artificial intelligence in space exploration and human settlement engineering
Apr 29, 2024 pm 03:25 PM
In the 1950s, artificial intelligence (AI) was born. That's when researchers discovered that machines could perform human-like tasks, such as thinking. Later, in the 1960s, the U.S. Department of Defense funded artificial intelligence and established laboratories for further development. Researchers are finding applications for artificial intelligence in many areas, such as space exploration and survival in extreme environments. Space exploration is the study of the universe, which covers the entire universe beyond the earth. Space is classified as an extreme environment because its conditions are different from those on Earth. To survive in space, many factors must be considered and precautions must be taken. Scientists and researchers believe that exploring space and understanding the current state of everything can help understand how the universe works and prepare for potential environmental crises
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Machine learning is an important branch of artificial intelligence that gives computers the ability to learn from data and improve their capabilities without being explicitly programmed. Machine learning has a wide range of applications in various fields, from image recognition and natural language processing to recommendation systems and fraud detection, and it is changing the way we live. There are many different methods and theories in the field of machine learning, among which the five most influential methods are called the "Five Schools of Machine Learning". The five major schools are the symbolic school, the connectionist school, the evolutionary school, the Bayesian school and the analogy school. 1. Symbolism, also known as symbolism, emphasizes the use of symbols for logical reasoning and expression of knowledge. This school of thought believes that learning is a process of reverse deduction, through existing
 Explainable AI: Explaining complex AI/ML models
Jun 03, 2024 pm 10:08 PM
Explainable AI: Explaining complex AI/ML models
Jun 03, 2024 pm 10:08 PM
Translator | Reviewed by Li Rui | Chonglou Artificial intelligence (AI) and machine learning (ML) models are becoming increasingly complex today, and the output produced by these models is a black box – unable to be explained to stakeholders. Explainable AI (XAI) aims to solve this problem by enabling stakeholders to understand how these models work, ensuring they understand how these models actually make decisions, and ensuring transparency in AI systems, Trust and accountability to address this issue. This article explores various explainable artificial intelligence (XAI) techniques to illustrate their underlying principles. Several reasons why explainable AI is crucial Trust and transparency: For AI systems to be widely accepted and trusted, users need to understand how decisions are made
 To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
Editor |ScienceAI Question Answering (QA) data set plays a vital role in promoting natural language processing (NLP) research. High-quality QA data sets can not only be used to fine-tune models, but also effectively evaluate the capabilities of large language models (LLM), especially the ability to understand and reason about scientific knowledge. Although there are currently many scientific QA data sets covering medicine, chemistry, biology and other fields, these data sets still have some shortcomings. First, the data form is relatively simple, most of which are multiple-choice questions. They are easy to evaluate, but limit the model's answer selection range and cannot fully test the model's ability to answer scientific questions. In contrast, open-ended Q&A




