Quantum algorithms conquer a new kind of problem!
In 1994, a mathematician figured out how to make quantum computers do things that ordinary classical computers cannot. The work shows that, in principle, a machine based on the rules of quantum mechanics can efficiently decompose large numbers into their principal factors - a very difficult task for classical computers, which make up most of today's Fundamentals of Internet Security.
#With it came a wave of optimism. Perhaps, researchers believe, we will be able to invent quantum algorithms that can solve a large number of different problems.
#But progress has stalled. "It's kind of disappointing," said Ryan O'Donnell of Carnegie Mellon University. "People are going to say, 'This is great, I'm sure we're going to get all kinds of other amazing algorithms,' and they're not." The scientists only found significant speedups for a single, narrow class of problems in a standard set called NP, meaning they have efficient verifiable solutions - such as factorization.
This has been the case for the past three years. Then in April, researchers invented an entirely new kind of problem that quantum computers should be able to solve faster than classical computers. It involves calculating the input of a complex mathematical process based only on its messy output. Whether this problem stands alone or is the first of many others remains to be determined.
"There is a sense of excitement," said Vinod Vaikuntanathan, a computer scientist at MIT. "A lot of people are thinking about what else is out there."
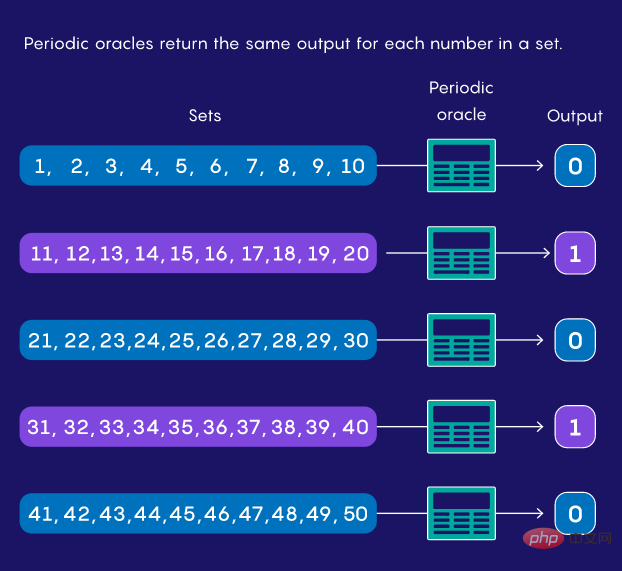
Computer scientists try to understand what quantum computers do better by studying the mathematical models that represent them. Typically, they imagine a model of a quantum or classical computer paired with an ideal computer called an oracle. An oracle is like a simple mathematical function or computer program that takes input and outputs a predetermined output.
They may have random behavior, outputting "yes" if the input is within some random range (for example, 12 to 67) and "no" otherwise. Or they might be periodic, so input between 1 and 10 returns "yes", 11 to 20 produces "no", 21 to 30 again produces "yes", and so on.
#Suppose you have one of these periodic prophecies, but you don't know the period. All you can do is feed it numbers and see what it outputs. How fast can a computer find cycles under these constraints? In 1993, Daniel Simon, then at the University of Montreal, discovered that quantum algorithms could compute answers to closely related problems faster than any classical algorithm.
This result allowed Simon to identify one of the first signs of where quantum computers would have significant advantages. But when he submitted his paper to a major conference, it was rejected. The paper did, however, pique the interest of a junior member of the conference program committee, Peter Shor, who was then working at Bell Laboratories in New Jersey.
Shor went on to discover that he could tweak Simon's algorithm to calculate the period of the oracle, if it had one. Then he realized he could tweak the algorithm again to solve an equation that behaved like a periodic prophecy: an equation describing factorization that was periodic.
Shor’s results were historic. The quantum algorithm he discovered can quickly reduce huge numbers to their constituent prime factors, something no known classical algorithm can do. In subsequent years, researchers discovered other efficient quantum algorithms. Some of them, like Shor's algorithm, even provide exponential advantages, but no one has been able to prove a significant quantum advantage on any non-periodic NP problem.
#The lack of progress prompted two computer scientists, Scott Aaronson of the University of Texas at Austin and Andris Ambainis of the University of Latvia, to observe. Proofs of quantum advantage always seem to rely on predictions with some non-random structure, such as periodicity. In 2009, they speculated that there would be no significant speedup for random or unstructured NP problems; no one could find exceptions.
Their conjectures limit the capabilities of quantum computers. But it only says that for certain types of unstructured NP problems—those with yes or no answers—there is no significant speedup. This conjecture does not apply if a problem involves finding a more specific, quantitative answer, a so-called search problem.
With this in mind, researchers Takashi Yamakawa of NTT's Social Informatics Laboratory and Mark Zhandry of NTT Research and Princeton University decided to investigate a project developed by Oded Regev in Experiment with specific search questions posed in 2005.
#Imagine a set of weathervanes that all point in the same direction. Give them each a measured push and let the gust influence their direction. Regev wants to determine where they were originally pointed based on their final direction. Problems like this came to be known as "error learning" because thrust and wind act as random sources of error in the original direction. There is evidence that both classical and quantum algorithms are difficult to solve.
Yamakawa and Zhandry tweaked the settings. They modified the power of these starts to make them more predictable. They also made the wind determined by a random oracle, so in some cases it's even more random, but in other cases completely dormant.
#With these modifications, the researchers found that the quantum algorithm could effectively find the initial direction. They also proved that any classical algorithm must be slowed down by an exponential factor. Like Shor, they then adapted the algorithm to solve a realistic version of the problem, replacing the predictions with actual mathematical equations.
Computer scientists are still trying to understand and solve this problem. Vaikuntanathan compared this to a different situation that occurs when doing data compression: when information is compressed, two bits can accidentally squeeze into the same place, thus overwriting them. The problems of anticipating these collisions in advance so as to avoid them have some similarities. "This is a class of problems that basically look like this," he said. "Maybe these problems can be solved quantumly."
People hope, Even on today's fledgling versions of quantum computers, unstructured problems like novel problems can be solved, providing a way to test them. The idea was that unstructured problems might require fewer resources to program or be less sensitive to noise because they are already random. But so far, this new problem still seems too advanced for existing quantum computers to solve. "It's a weird question. I didn't think about defining it," Aaronson said, "but in retrospect, it has some really nice features."
This result provides the first example of significant quantum advantage on an unstructured NP problem. Will many other problems in the quantum world go from being nearly unsolvable to solvable? Now there are even more reasons to think so. “This to some extent changes our view of what problems quantum computers are good at solving,” O’Donnell said.
The above is the detailed content of Quantum algorithms conquer a new kind of problem!. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
 CUDA's universal matrix multiplication: from entry to proficiency!
Mar 25, 2024 pm 12:30 PM
CUDA's universal matrix multiplication: from entry to proficiency!
Mar 25, 2024 pm 12:30 PM
General Matrix Multiplication (GEMM) is a vital part of many applications and algorithms, and is also one of the important indicators for evaluating computer hardware performance. In-depth research and optimization of the implementation of GEMM can help us better understand high-performance computing and the relationship between software and hardware systems. In computer science, effective optimization of GEMM can increase computing speed and save resources, which is crucial to improving the overall performance of a computer system. An in-depth understanding of the working principle and optimization method of GEMM will help us better utilize the potential of modern computing hardware and provide more efficient solutions for various complex computing tasks. By optimizing the performance of GEMM
 How to calculate addition, subtraction, multiplication and division in word document
Mar 19, 2024 pm 08:13 PM
How to calculate addition, subtraction, multiplication and division in word document
Mar 19, 2024 pm 08:13 PM
WORD is a powerful word processor. We can use word to edit various texts. In Excel tables, we have mastered the calculation methods of addition, subtraction and multipliers. So if we need to calculate the addition of numerical values in Word tables, How to subtract the multiplier? Can I only use a calculator to calculate it? The answer is of course no, WORD can also do it. Today I will teach you how to use formulas to calculate basic operations such as addition, subtraction, multiplication and division in tables in Word documents. Let's learn together. So, today let me demonstrate in detail how to calculate addition, subtraction, multiplication and division in a WORD document? Step 1: Open a WORD, click [Table] under [Insert] on the toolbar, and insert a table in the drop-down menu.
 How to count the number of elements in a list using Python's count() function
Nov 18, 2023 pm 02:53 PM
How to count the number of elements in a list using Python's count() function
Nov 18, 2023 pm 02:53 PM
How to use Python's count() function to calculate the number of an element in a list requires specific code examples. As a powerful and easy-to-learn programming language, Python provides many built-in functions to handle different data structures. One of them is the count() function, which can be used to count the number of elements in a list. In this article, we will explain how to use the count() function in detail and provide specific code examples. The count() function is a built-in function of Python, used to calculate a certain
 Count the number of occurrences of a substring recursively in Java
Sep 17, 2023 pm 07:49 PM
Count the number of occurrences of a substring recursively in Java
Sep 17, 2023 pm 07:49 PM
Given two strings str_1 and str_2. The goal is to count the number of occurrences of substring str2 in string str1 using a recursive procedure. A recursive function is a function that calls itself within its definition. If str1 is "Iknowthatyouknowthatiknow" and str2 is "know" the number of occurrences is -3. Let us understand through examples. For example, input str1="TPisTPareTPamTP", str2="TP"; output Countofoccurrencesofasubstringrecursi
 How to use the Math.Pow function in C# to calculate the power of a specified number
Nov 18, 2023 am 11:32 AM
How to use the Math.Pow function in C# to calculate the power of a specified number
Nov 18, 2023 am 11:32 AM
In C#, there is a Math class library, which contains many mathematical functions. These include the function Math.Pow, which calculates powers, which can help us calculate the power of a specified number. The usage of the Math.Pow function is very simple, you only need to specify the base and exponent. The syntax is as follows: Math.Pow(base,exponent); where base represents the base and exponent represents the exponent. This function returns a double type result, that is, the power calculation result. Let's
 Java program to calculate the area of a triangle using determinants
Aug 31, 2023 am 10:17 AM
Java program to calculate the area of a triangle using determinants
Aug 31, 2023 am 10:17 AM
Introduction The Java program for calculating the area of a triangle using determinants is a concise and efficient program that can calculate the area of a triangle given the coordinates of three vertices. This program is useful for anyone learning or working with geometry, as it demonstrates how to use basic arithmetic and algebraic calculations in Java, as well as how to use the Scanner class to read user input. The program prompts the user for the coordinates of three points of the triangle, which are then read in and used to calculate the determinant of the coordinate matrix. Use the absolute value of the determinant to ensure the area is always positive, then use a formula to calculate the area of the triangle and display it to the user. The program can be easily modified to accept input in different formats or to perform additional calculations, making it a versatile tool for geometric calculations. ranks of determinants
 Python program to calculate the sum of the right diagonal elements of a matrix
Aug 19, 2023 am 11:29 AM
Python program to calculate the sum of the right diagonal elements of a matrix
Aug 19, 2023 am 11:29 AM
A popular general-purpose programming language is Python. It is used in a variety of industries, including desktop applications, web development, and machine learning. Fortunately, Python has a simple and easy-to-understand syntax that is suitable for beginners. In this article, we will use Python to calculate the sum of the right diagonal of a matrix. What is a matrix? In mathematics, we use a rectangular array or matrix to describe a mathematical object or its properties. It is a rectangular array or table containing numbers, symbols, or expressions arranged in rows and columns. . For example -234512367574 Therefore, this is a matrix with 3 rows and 4 columns, expressed as a 3*4 matrix. Now, there are two diagonals in the matrix, the primary diagonal and the secondary diagonal
 Java program example to calculate total score and percentage
Sep 11, 2023 pm 06:01 PM
Java program example to calculate total score and percentage
Sep 11, 2023 pm 06:01 PM
We will demonstrate how to calculate total scores and percentages using a Java program. Total score refers to the sum of all available scores, while the term percentage refers to the calculated score divided by the total score and multiplied by the resulting number 100. percentage_of_marks=(obtained_marks/total_marks)×100 Example 1 This is a Java program that demonstrates how to calculate total scores and percentages. //JavaProgramtodemonstratehowisTotalmarksandPercentagescalculatedimportjava.io.*;publicclassTotalMarks_




