
The implementation data structure of the int type inside cpython is as follows:
typedef struct _longobject PyLongObject;
struct _longobject {
PyObject_VAR_HEAD
digit ob_digit[1];
};
#define PyObject_VAR_HEAD PyVarObject ob_base;
typedef struct {
PyObject ob_base;
Py_ssize_t ob_size; /* Number of items in variable part */
} PyVarObject;
typedef struct _object {
_PyObject_HEAD_EXTRA
Py_ssize_t ob_refcnt;
struct _typeobject *ob_type;
} PyObject;The above data structure is represented graphically as shown below:
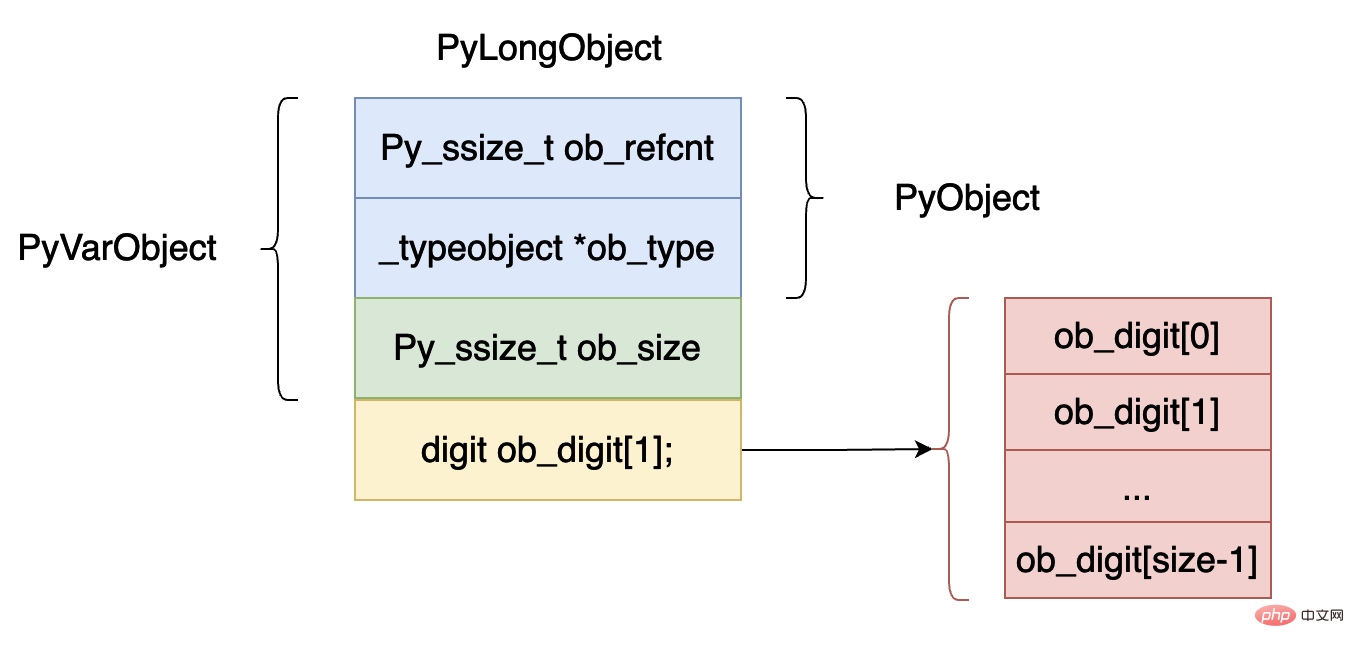
ob_refcnt represents the number of reference counts of the object. This is very useful for garbage collection. Later we will analyze the garbage collection part of the virtual machine in depth. .
ob_type, indicates the data type of this object. In python, sometimes it is necessary to judge the data type of the data. For example, the two keywords of isinstance and type will be used. field.
ob_size, this field indicates how many elements there are in this integer object array ob_digit.
The digit type is actually a macro definition of the uint32_t type, representing 32-bit integer data.
First of all, we know that integers in python will not overflow. This is why PyLongObject uses arrays. In the internal implementation of cpython, integers include 0, positive numbers, and negative numbers. Regarding this, there are the following regulations in cpython:
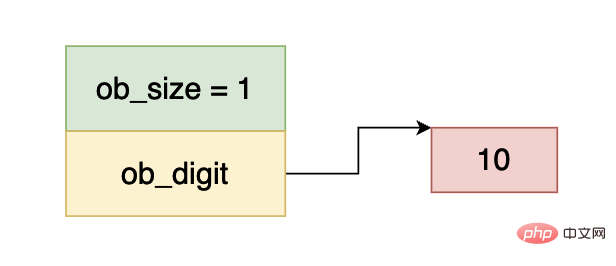
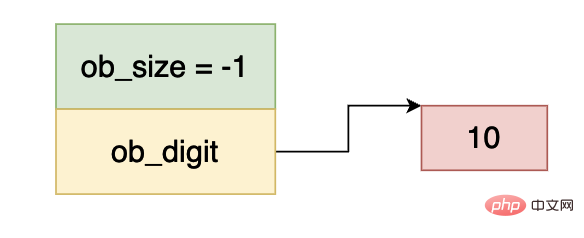

0 1⋅21 1⋅22 ... 1⋅229 0⋅230 0⋅231 1⋅232
Because we only use the first 30 bits for each array element, so the second integer data corresponds to 230, everyone You can understand the entire calculation process based on the above results.
0 1⋅21 1⋅22 ... 1⋅229 0⋅230 0⋅231 1⋅2 32)
Small integer poolIn order to avoid frequently creating some commonly used integers and speed up program execution, we can cache some commonly used integers first, if necessary Just return this data directly. The relevant code in cpython is as follows: (The interval of cached data in the small integer pool is [-5, 256])#define NSMALLPOSINTS 257 #define NSMALLNEGINTS 5 static PyLongObject small_ints[NSMALLNEGINTS + NSMALLPOSINTS];
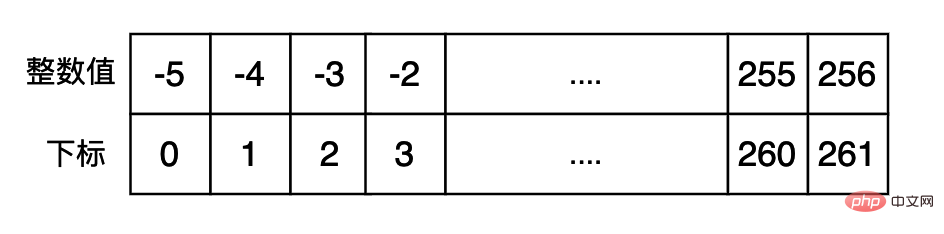
>>> a = 1 >>> b = 2 >>> c = 1 >>> id(a), id(c) (4343136496, 4343136496) >>> a = -6 >>> c = -6 >>> id(a), id(c) (4346020624, 4346021072) >>> a = 257 >>> b = 257 >>> id(a), id(c) (4346021104, 4346021072) >>>
>>> a = -5 >>> b = 256 >>> (id(b) - id(a)) / 261 32.0 >>>
#include "Python.h"
#include <stdio.h>
int main()
{
printf("%ld\n", sizeof(PyLongObject));
return 0;
}
static PyObject *
get_small_int(sdigit ival)
{
PyObject *v;
assert(-NSMALLNEGINTS <= ival && ival < NSMALLPOSINTS);
v = (PyObject *)&small_ints[ival + NSMALLNEGINTS];
Py_INCREF(v);
return v;
}如果你了解过大整数加法就能够知道,大整数加法的具体实现过程了,在 cpython 内部的实现方式其实也是一样的,就是不断的进行加法操作然后进行进位操作。
#define Py_ABS(x) ((x) < 0 ? -(x) : (x)) // 返回 x 的绝对值
#define PyLong_BASE ((digit)1 << PyLong_SHIFT)
#define PyLong_MASK ((digit)(PyLong_BASE - 1))
static PyLongObject *
x_add(PyLongObject *a, PyLongObject *b)
{
// 首先获得两个整型数据的 size
Py_ssize_t size_a = Py_ABS(Py_SIZE(a)), size_b = Py_ABS(Py_SIZE(b));
PyLongObject *z;
Py_ssize_t i;
digit carry = 0;
// 确保 a 保存的数据 size 是更大的
/* Ensure a is the larger of the two: */
if (size_a < size_b) {
{ PyLongObject *temp = a; a = b; b = temp; }
{ Py_ssize_t size_temp = size_a;
size_a = size_b;
size_b = size_temp; }
}
// 创建一个新的 PyLongObject 对象,而且数组的长度是 size_a + 1
z = _PyLong_New(size_a+1);
if (z == NULL)
return NULL;
// 下面就是整个加法操作的核心
for (i = 0; i < size_b; ++i) {
carry += a->ob_digit[i] + b->ob_digit[i];
// 将低 30 位的数据保存下来
z->ob_digit[i] = carry & PyLong_MASK;
// 将 carry 右移 30 位,如果上面的加法有进位的话 刚好可以在下一次加法当中使用(注意上面的 carry)
// 使用的是 += 而不是 =
carry >>= PyLong_SHIFT; // PyLong_SHIFT = 30
}
// 将剩下的长度保存 (因为 a 的 size 是比 b 大的)
for (; i < size_a; ++i) {
carry += a->ob_digit[i];
z->ob_digit[i] = carry & PyLong_MASK;
carry >>= PyLong_SHIFT;
}
// 最后保存高位的进位
z->ob_digit[i] = carry;
return long_normalize(z); // long_normalize 这个函数的主要功能是保证 ob_size 保存的是真正的数据的长度 因为可以是一个正数加上一个负数 size 还变小了
}
PyLongObject *
_PyLong_New(Py_ssize_t size)
{
PyLongObject *result;
/* Number of bytes needed is: offsetof(PyLongObject, ob_digit) +
sizeof(digit)*size. Previous incarnations of this code used
sizeof(PyVarObject) instead of the offsetof, but this risks being
incorrect in the presence of padding between the PyVarObject header
and the digits. */
if (size > (Py_ssize_t)MAX_LONG_DIGITS) {
PyErr_SetString(PyExc_OverflowError,
"too many digits in integer");
return NULL;
}
// offsetof 会调用 gcc 的一个内嵌函数 __builtin_offsetof
// offsetof(PyLongObject, ob_digit) 这个功能是得到 PyLongObject 对象 字段 ob_digit 之前的所有字段所占的内存空间的大小
result = PyObject_MALLOC(offsetof(PyLongObject, ob_digit) +
size*sizeof(digit));
if (!result) {
PyErr_NoMemory();
return NULL;
}
// 将对象的 result 的引用计数设置成 1
return (PyLongObject*)PyObject_INIT_VAR(result, &PyLong_Type, size);
}
static PyLongObject *
long_normalize(PyLongObject *v)
{
Py_ssize_t j = Py_ABS(Py_SIZE(v));
Py_ssize_t i = j;
while (i > 0 && v->ob_digit[i-1] == 0)
--i;
if (i != j)
Py_SIZE(v) = (Py_SIZE(v) < 0) ? -(i) : i;
return v;
}The above is the detailed content of What is the implementation principle of integers in the Python virtual machine?. For more information, please follow other related articles on the PHP Chinese website!




