Reinforcement learning discovers matrix multiplication algorithm, DeepMind appears on the cover of Nature and launches AlphaTensor

Algorithms have been helping mathematicians perform basic operations for thousands of years. Long ago, the ancient Egyptians invented an algorithm for multiplying two numbers without the need for a multiplication table. The Greek mathematician Euclid described an algorithm for calculating the greatest common divisor that is still used today. During the Islamic Golden Age, Persian mathematician Muhammad ibn Musa al-Khwarizmi devised a new algorithm for solving linear and quadratic equations that would have a profound impact on subsequent research.

In fact, there is a saying about the emergence of the word algorithm: the word al-Khwarizmi in the name of the Persian mathematician Muhammad ibn Musa al-Khwarizmi is translated into Latin as Algoritmi meaning, which leads to the word algorithm. However, although today we are very familiar with algorithms, we can learn them in the classroom, and often encounter them in the field of scientific research. It seems that the entire society is using algorithms, but the process of discovering new algorithms is very difficult. ​

Now, DeepMind uses AI to discover new algorithms.

In the latest issue of Nature's cover paper "Discovering faster matrix multiplication algorithms with reinforcement learning", DeepMind proposed AlphaTensor and stated that it is the first one that can be used for basic functions such as matrix multiplication. Artificial intelligence systems tasked with discovering novel, efficient, and provably correct algorithms. Simply put, using AlphaTensor enables you to discover new algorithms. The research sheds light on a 50-year-old unresolved problem in mathematics: finding the fastest way to multiply two matrices.

• ##Paper address ：https://www.nature.com/articles/s41586-022-05172-4
• GitHub address: https://github.com/deepmind /alphatensor​

AlphaTensor is built on the basis of AlphaZero, which is a chess, Agents that can beat humans in board games like Go and Shogi. This work demonstrates AlphaZero's transition from being used for games to being used for the first time to solve unsolved mathematical problems. ​​

Matrix Multiplication

Matrix multiplication is one of the simplest operations in algebra and is typically taught in high school math classes. But outside the classroom, this humble mathematical operation has had a huge impact in the contemporary digital world and is ubiquitous in modern computing.

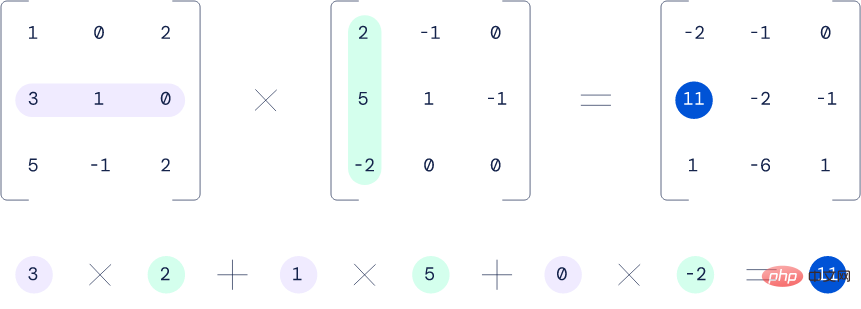
Example of multiplying two 3x3 matrices. ​

You may not have noticed that matrix multiplication is hidden everywhere in our lives, such as image processing in smartphones, recognizing voice commands, It performs calculations behind the scenes such as generating graphics for computer games. Companies all over the world are willing to spend huge amounts of time and money developing computing hardware to solve matrix multiplication efficiently. Therefore, even small improvements in matrix multiplication efficiency can have widespread effects.

For centuries, mathematicians believed that the standard matrix multiplication algorithm was the most efficient algorithm. But in 1969, German mathematician Volken Strassen shocked the mathematical world by proving that a better algorithm did exist.

Comparing the standard algorithm with the Strassen algorithm, the latter performs one less multiplication operation, which is 7 times. The former requires 8 times, and the overall efficiency is greatly improved. ​

By studying very small matrices (size 2x2), Strassen discovered a clever way to combine the terms of the matrix to produce a larger Fast algorithm. In the following decades, researchers have been studying larger matrices, and even finding an efficient method for multiplying 3x3 matrices has not yet been solved. ​

New research from DeepMind explores how modern AI technology is driving the automatic discovery of new matrix multiplication algorithms. Based on advances in human intuition, the algorithm discovered by AlphaTensor is more efficient than many SOTA methods for larger matrices. The study shows that AI-designed algorithms outperform those designed by humans, an important step forward in the field of algorithm discovery.

The process and progress of algorithm discovery automation

First convert the problem of discovering efficient algorithms for matrix multiplication into a single-player game. Among them, board is a three-dimensional tensor (array of numbers) used to capture how correct the current algorithm is. Through a set of allowed moves corresponding to the algorithm's instructions, the player attempts to modify the tensor and return its entries to zero.

When the player manages to do this, a provably correct matrix multiplication algorithm is generated for any pair of matrices, and its efficiency is measured by the number of steps taken to zero out the tensor.

This game is very challenging and the number of possible algorithms to consider is far greater than the number of atoms in the universe, even for a case as small as matrix multiplication. Compared to the game of Go, which has been an AI challenge for decades, the game has 30 orders of magnitude more possible moves per move (one setting DeepMind considered was 10^33+.)

To address the challenges of this domain that is significantly different from traditional games, DeepMind developed several key components, including a new neural network architecture that incorporates problem-specific inductive biases, a program to generate useful synthetic data, and a A way to take advantage of the symmetry of the problem.

Next, DeepMind trained a reinforcement learning agent, AlphaTensor, to play the game, starting with no knowledge of existing matrix multiplication algorithms. By learning, AlphaTensor gradually improves over time, rediscovering historically fast matrix algorithms (such as Strassen's algorithm) and discovering algorithms that are faster than previously known.

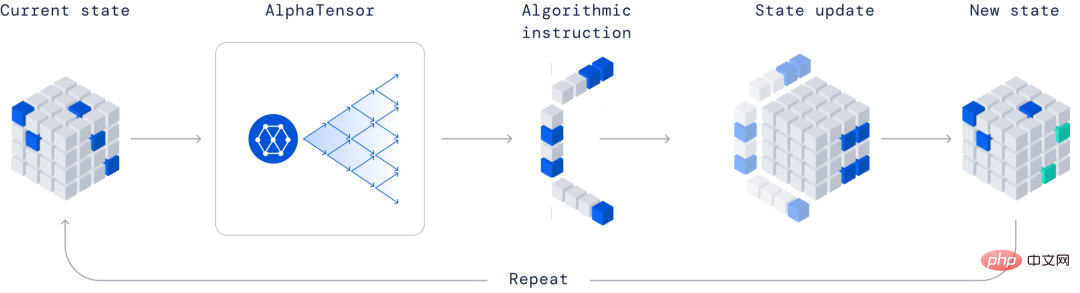
AlphaTensor A single player game where the goal is to find the correct matrix multiplication algorithm. The game state is a cubic array of numbers (gray represents 0, blue represents 1, and green represents - 1) that represents the remaining work to be done. ​

For example, if the traditional algorithm taught in school can use 100 multiplications to complete the multiplication of 4x5 and 5x5 matrices, through human intelligence Wisdom can bring that number down to 80 times. In comparison, the algorithm discovered by AlphaTensor accomplishes the same operation using only 76 multiplications, as shown in the image below.

In addition to the above examples, the algorithm discovered by AlphaTensor also improves Strassen's second-order algorithm in a finite field for the first time. algorithm. These algorithms for multiplying small matrices can be used as primitives to multiply larger matrices of any size.

AlphaTensor also discovered a diverse set of algorithms with SOTA complexity, with thousands of matrix multiplication algorithms of each size, indicating that the space of matrix multiplication algorithms is larger than previously thought. Rich. ​

Algorithms in this rich space have different mathematical and practical properties. Taking advantage of this diversity, DeepMind tuned AlphaTensor to specifically discover algorithms that run fast on given hardware (e.g., Nvidia V100 GPU, Google TPU v2). These algorithms perform large matrix multiplications 10-20% faster than commonly used algorithms on the same hardware, demonstrating AlphaTensor's flexibility in optimizing arbitrary objectives.

#AlphaTensor has a target that corresponds to the algorithm runtime. When the correct matrix multiplication algorithm is discovered, it is benchmarked on the specified hardware and then fed back to AlphaTensor to learn a more efficient algorithm on the specified hardware.

Implications for future research and applications

From a mathematical perspective, DeepMind's results could guide complexity theory, which aims to identify the fastest algorithms for solving computational problems. further research. AlphaTensor helps deepen our understanding of the richness of matrix multiplication algorithms by exploring the space of possible algorithms more efficiently than previous methods.

Additionally, because matrix multiplication is a core component of many computing tasks, including computer graphics, digital communications, neural network training, and scientific computing, the algorithms discovered by AlphaTensor can significantly improve these fields. computational efficiency. ​

Although this article only focuses on the specific problem of matrix multiplication, DeepMind hopes to inspire more people to use AI to guide algorithm discovery for other basic computing tasks. Moreover, DeepMind’s research also shows that AlphaZero’s powerful algorithm goes far beyond the realm of traditional games and can help solve open problems in the field of mathematics.

In the future, DeepMind hopes to use more artificial intelligence to help society solve some of the most important challenges in mathematics and science based on their research.

The above is the detailed content of Reinforcement learning discovers matrix multiplication algorithm, DeepMind appears on the cover of Nature and launches AlphaTensor. For more information, please follow other related articles on the PHP Chinese website!