 Java
Java
 javaTutorial
javaTutorial
 How to use custom classes to encapsulate arrays in Java to implement data operations
How to use custom classes to encapsulate arrays in Java to implement data operations
How to use custom classes to encapsulate arrays in Java to implement data operations
As a basic data storage structure, arrays are widely used. An array is a data structure that uses continuous memory space to store fixed length and the same data type. The data structure is language-independent. Here, Java is used to perform array-related operations. Array indexes start from 0.
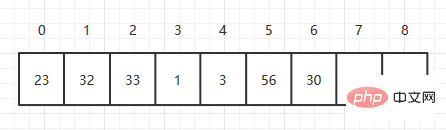
Array initialization
There are two ways to create data. One is to declare a fixed-length data first, and then assign a value to the array. The other is to The first is direct assignment.
First type:
数据类型[] 数组名称 = new 数据类型[长度];
The [] mark here declares an array. In addition to being placed after the data type, this [] can also be placed behind the array. After the noun, the effect is the same. If I declare an array of type long with a length of 2, and assign the value:
long[] arr = new long[2]; arr[0] = 1; arr[1] = 2;
The second :
数据类型[] 数组名称 = {元素1,元素2, ...};In this way, the array is assigned a value directly when it is initialized. The length of the array is determined by the number of elements.
Two custom classes encapsulate arrays to implement data operations
public class MyArray {
// 自定义数组 private long[] arr;
// 有效数据长度 private int element;
public MyArray(){
arr = new long[9];
}
public MyArray(int maxsize){
arr = new long[maxsize];
}
/**
* 显示数组元素
*/ public void display(){
System.out.print("[");
for (int i = 0; i < element; i++) {
System.out.print(arr[i]+" ");
}
System.out.print("]");
}
}2.1 Add elements
Arrays use continuous memory space to store data, so every time they are added, Add an element to the last element of the current array. You can add elements at once, so its complexity is O(1). If you define an array with a length of 9, there are already two elements in the array. , then add the third element as follows:
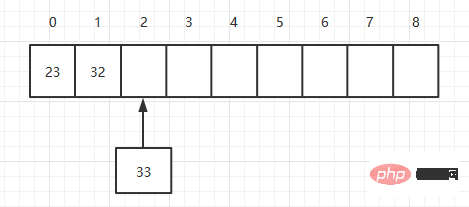
public void add(long value){
arr[element] = value;
element++;
}2.2 Query the element position based on the value
This search method is also called linear search, which is based on the incoming The value loops through the elements to obtain the corresponding position. In theory, it takes N/2 times to query an element on average, so its complexity is O(N).
public int find(long value){
int i;
for (i = 0; i < element; i++) {
if(value == arr[i]){
break;
}
}
if(i == element){
return -1;
}else {
return i;
}
}2.3 Query elements according to index
To find elements according to index, that is, to obtain the element at the corresponding position, the complexity is O(1).
public long get(int index){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
return arr[index];
}
}2.4 Delete elements based on index
After deleting the element corresponding to the index, we need to move all elements after the index forward one position. If I want to delete the element with index 2, as follows:
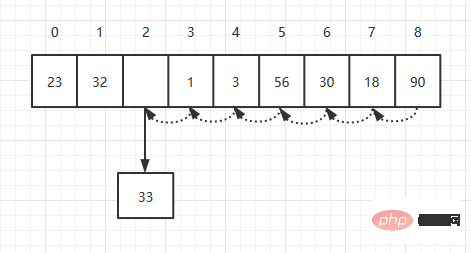
# Theoretically, to delete an element on average, we need to move N/2 times, so its time complexity is also O(N).
public void delete(int index){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
for (int i = index; i < element; i++) {
arr[index] = arr[index+1];
}
element --;
}
}2.5 Modify elements
Modify the element at a certain position and modify the corresponding element directly according to the index once, so its time complexity is O(1).
public void change(int index,long newValue){
if(index >= element || index < 0){
throw new ArrayIndexOutOfBoundsException();
}else {
arr[index] = newValue;
}
}3 Ordered array
Ordered array is a special type of array. The elements in the ordered array are arranged in a certain order.
3.1 Add elements
When adding elements, add elements to a certain position in order. As follows, add an element 33 to an array.
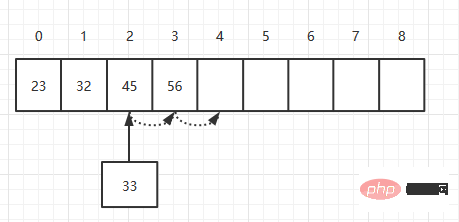
First, move the element with index 3 to index 4, then move the element with index 2 to index 3, and finally add 33 to index 2. Theoretically, inserting an element requires moving N/2 elements, so its time complexity is O(N).
public void add(long value){
int i;
for (i = 0; i < element; i++) {
if(arr[i]>value){
break;
}
}
for (int j = element; j > i; j--){
arr[j] = arr[j-1];
}
arr[i] = value;
element++;
}3.2 Dichotomy method to query index based on elements
In an unordered array, use the linear method to find related elements. The linear method is to search one by one according to the index. Sorted arrays can use the dichotomy method to find elements. Dichotomy means dividing an array into two from the middle, determining which array the element is in, and then repeating this operation.
Suppose there is an array with 8 elements. The content of the array is an ordered sequence of 0-7. To find the element 5, it is divided into 0-3 and 4-7 for the first time. Two arrays, then divide 4-7 into two arrays 4-5 and 6-7, and finally divide 4-5 into 4 and 5 to query the specific elements. In this way, after dividing 3 times, you can query the length of The complexity of specific elements in an array of 8 is O(logN) (the base of logN in computers generally refers to 2, which means that the power of 2 is equal to n).
public int search(long value){
// 中间值 int middle = 0;
// 最小值 int low = 0;
// 最大值 int pow = element;
while (true){
middle = (low + pow) / 2;
if(arr[middle] == value){
return middle;
}else if (low > pow){
return -1;
}else{
if(arr[middle] > value){
pow = middle - 1;
}else{
low = middle + 1;
}
}
}
}Four Summary
The lower the complexity means the algorithm is better, so O(1) > O(logN) > O(N) > O(N^2) .
| Algorithm | Complexity |
|---|---|
| Linear search | O(N) |
| Binary search | O(logN) |
| Unordered array insertion | O(1) |
| Ordered array insertion | O(N) |
| Unordered array deletion | O(N) |
| Ordered array deletion | O(N) |
Unordered array insertion is fast, search and deletion are slow
Ordered array search is fast, insertion and deletion are slow
The above is the detailed content of How to use custom classes to encapsulate arrays in Java to implement data operations. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1376
1376
 52
52
 Square Root in Java
Aug 30, 2024 pm 04:26 PM
Square Root in Java
Aug 30, 2024 pm 04:26 PM
Guide to Square Root in Java. Here we discuss how Square Root works in Java with example and its code implementation respectively.
 Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Perfect Number in Java. Here we discuss the Definition, How to check Perfect number in Java?, examples with code implementation.
 Random Number Generator in Java
Aug 30, 2024 pm 04:27 PM
Random Number Generator in Java
Aug 30, 2024 pm 04:27 PM
Guide to Random Number Generator in Java. Here we discuss Functions in Java with examples and two different Generators with ther examples.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Guide to Weka in Java. Here we discuss the Introduction, how to use weka java, the type of platform, and advantages with examples.
 Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Smith Number in Java. Here we discuss the Definition, How to check smith number in Java? example with code implementation.
 Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
In this article, we have kept the most asked Java Spring Interview Questions with their detailed answers. So that you can crack the interview.
 Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Java 8 introduces the Stream API, providing a powerful and expressive way to process data collections. However, a common question when using Stream is: How to break or return from a forEach operation? Traditional loops allow for early interruption or return, but Stream's forEach method does not directly support this method. This article will explain the reasons and explore alternative methods for implementing premature termination in Stream processing systems. Further reading: Java Stream API improvements Understand Stream forEach The forEach method is a terminal operation that performs one operation on each element in the Stream. Its design intention is
 TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
Guide to TimeStamp to Date in Java. Here we also discuss the introduction and how to convert timestamp to date in java along with examples.



