How to implement arctan conversion angle in Python

Cartesian coordinate system

For the plane coordinate system, the range of the angle θ between any ray OP and the x-axis can be [0,2π) or (-&pi ;,π], unless otherwise specified, we use the latter.
Represent the point in the Cartesian space coordinate system Pc = ( x , y , z ) into the spherical coordinate system The form of Ps = ( θ , ϕ , r ).

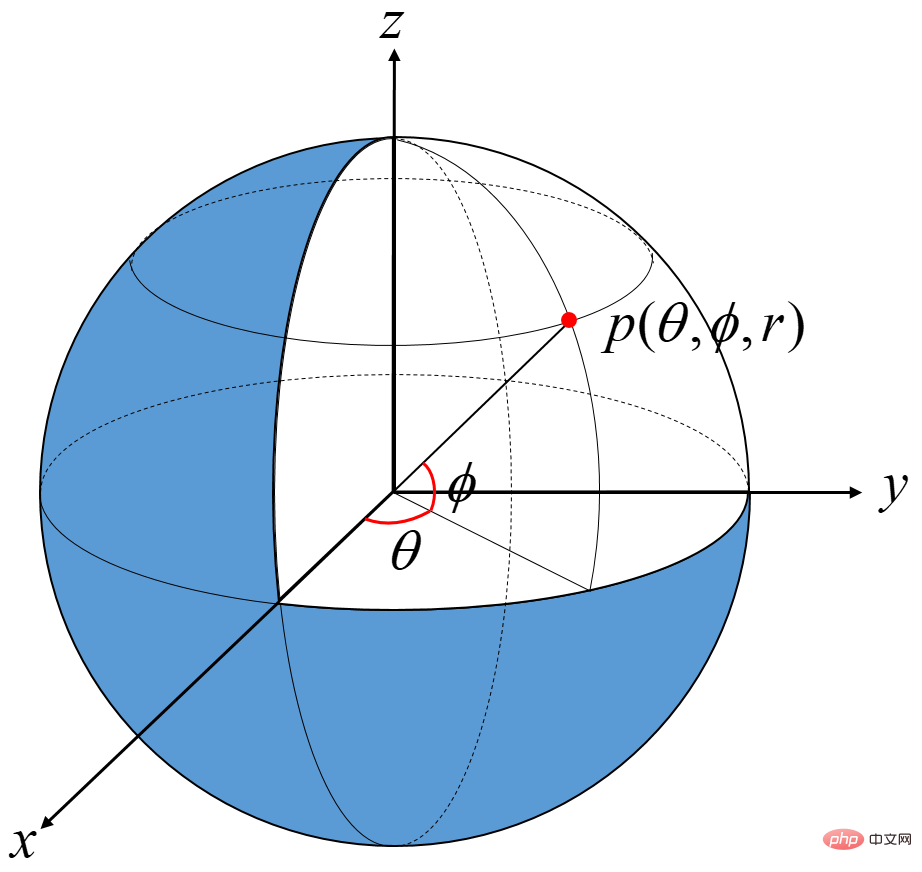
where

According to the definition of spherical coordinates, it is required that θ∈[−π,π], ϕ∈[−π/2,π/2], r∈[0, ∞).

Forθ, the period of the tangent function is π, so the arctangent function arctan generally only takes one period, its domain is R, and its value range is (−π /2, π/2). To solve this problem, the Arctan function, also known as the arctan2 function, was introduced.

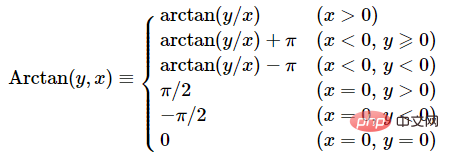
atan2 Function usage atan2(delta_y, delta_x)

import math
a = math.atan2(400,-692.820)
# 2.6179936760992044
angle = a/math.pi*180
# 149.99998843242386

atan Function usage atan(delta_y / delta_x)

import math
delta_y = 400
delta_x = -692.820

if delta_x == 0:
    b = math.pi / 2.0
    angle = b/math.pi*180
    if delta_y == 0:
        angle = 0.0
    elif delta_y < 0:
        angle -= 180
else:
    b =  math.atan(delta_y/delta_x) 
    angle = b/math.pi*180
    if delta_y > 0 and delta_x < 0:
        angle = angle + 180
    if delta_y < 0 and delta_x < 0:
        angle = angle - 180

b,angle
# (-0.5235989774905888, 149.99998843242386)

atan Similarities and differences with atan2

• The number of parameters is different

• The return value of both is radians

• If delta_x is equal to 0, atan2 can still be calculated, but atan needs to be judged in advance, otherwise it will cause a program error

• Quadrant processing

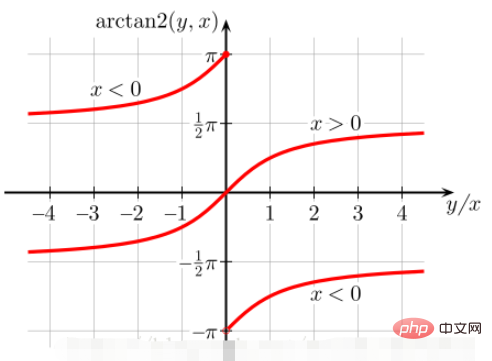
atan2(b,a) is the 4-quadrant arctangent. Its value depends not only on the tangent value b/a, but also on which quadrant the point (b,a) falls into:

• When point (b,a) falls into the first quadrant (b>0, a>0), the range of atan2(b,a) is 0 ~ pi /2

• ##When point (b,a) falls into the second quadrant (b>0, a<0), the range of atan2(b,a) is

  pi/2 ~ pi

• When point (b,a) falls into the third quadrant (b<0, a<0), atan2(b,a ) range is

  -pi~-pi/2

• When point (b, a) falls into the fourth quadrant (b<0, a>0) When, the range of atan2(b,a) is

  -pi/2～0

and atan(b/a) is a/b only based on the tangent value Find the corresponding angle (can be regarded as just the arc tangent of the two quadrants):

• When b/a > 0, the value range of atan(b/a) is

  0 ~ pi/2

• When b/a < 0, the value range of atan(b/a) is

  -pi/2~0

Value range

##Point(b ,a) When falling into
• the first quadrant (b>0, a>0)

  or the fourth quadrant (b<0, a>0), atan2(b ,a) = atan(b/a)

  ##Point (b,a) falls into
the second quadrant (b>0, a<0)
• , b/a<0, so the value range of atan(b/a) is always

  -pi/2~0, however, the range of atan2(b,a) is pi/2 ~ pi, so atan(b/a) needs to add 180 to calculate the angle value.

  Point (b,a) falls into the
third quadrant (b<0, a<0)
• , b/a>0, so atan(b/ a) The value range is

  0 ~ pi/2, and at this time the range of atan2(b,a) is -pi~-pi/2, so atan(b/a ) To calculate the angle value, subtract 180.

  Conclusion: atan and atan2 functions, it is recommended to use the atan2 function

The above is the detailed content of How to implement arctan conversion angle in Python. For more information, please follow other related articles on the PHP Chinese website!