What is the principle of merge sort algorithm in Java and how to implement it

1. Basic idea

Merge sort is an effective sorting algorithm based on merge operations. This algorithm is a very typical application using the divide and conquer method (Divide and Conquer). Merge the already ordered subsequences to obtain a completely ordered sequence; that is, first make each subsequence orderly, and then make the subsequence segments orderly. If two ordered lists are merged into one ordered list, it is called a 2-way merge.

2. Algorithm analysis

1. Algorithm description

Divide the input sequence of length n into two subsequences of length n/2; for these two subsequences Merge sorting is used respectively; two sorted subsequences are merged into a final sorting sequence.

2. Process Analysis

(1). Now we will split items [1] (index from 0 to 0, both sides included) and [28] index from 1 to 1, Both sides included) are merged together.

(2), because 1 (left split) <= 28 (right split), we copy {rightPart} into a new array.

(3) Since the left split is empty, we copy 28 (right split) into a new array.

(4). We copy the elements in the new array back to the original array.

(5), because 3 (left split) <= 21 (right split), we copy {rightPart} into a new array.

(6). Because the left split is empty, we copy 21 (right split) into a new array.

(7), Now we will split the terms [1,28] (index from 0 to 1, both sides included) and [3,21] with index from 2 to 3, both sides included) merged together.

(8), because 1 (left split) <= 3 (right split), we copy {rightPart} into a new array.

(9), because 28 (left split) > 3 (right split), we copy {rightPart} into a new array.

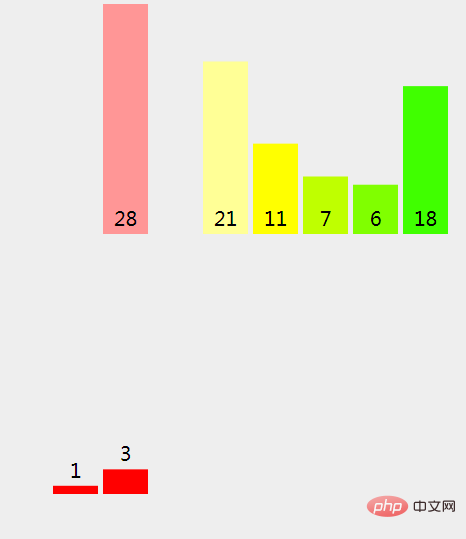
(10), because 28 (left split) > 21 (right split), we copy {rightPart} into a new array.

(11), because the right split is empty, we copy 28 (left split) into the new array.

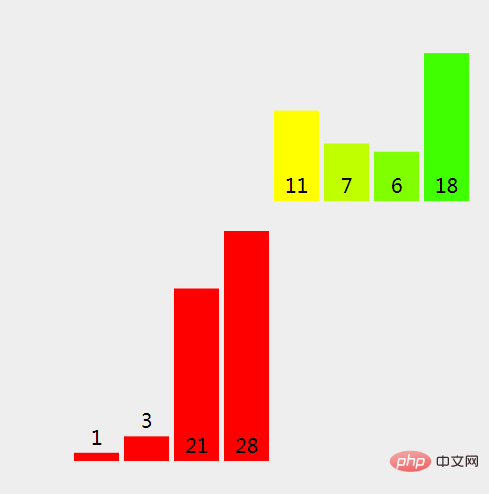
# (12), we copy the elements in the new array back to the original array.

(13), Now we will split the terms [11] (index from 4 to 4, both sides included) and [7] with index from 5 to 5, both sides All included) are merged together.

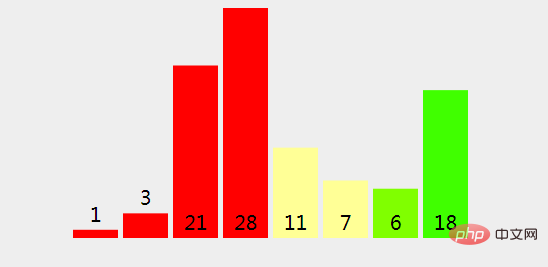
(14), because 11 (left split) > 7 (right split), we copy {rightPart} into a new array.

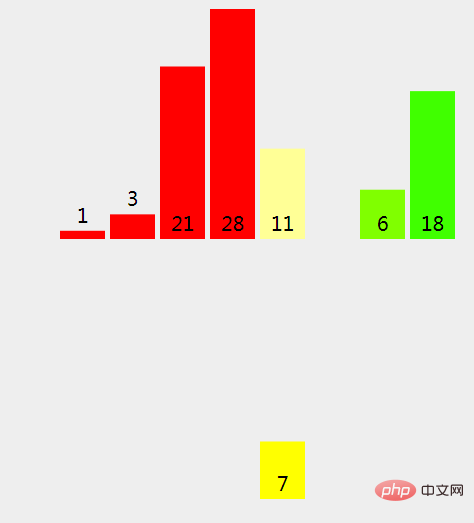
(15), because the right split is empty, we copy 11 (left split) into the new array.

(16). We copy the elements in the new array back to the original array.

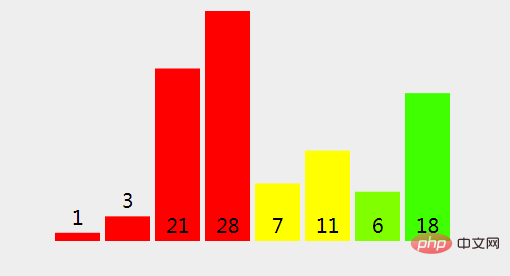
(17), and so on

(18), because 1 (left split) <= 6 (right split), we Copy {rightPart} into a new array.

(19), because 3 (left split) <= 6 (right split), we copy {rightPart} into a new array.

(20), because 21 (left split) > 6 (right split), we copy {rightPart} into a new array.

(21), because 21 (left split) > 7 (right split), we copy {rightPart} into a new array.

# (22), and so on, we copy the elements in the new array back to the original array.

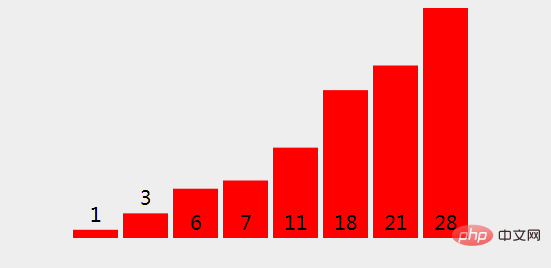
3. GIF demonstration

3. Algorithm implementation

package com.algorithm.tenSortingAlgorithm;

import java.util.Arrays;

public class MergeSort {
    private static void mergeSort(int[] arr, int low, int high) {
        if (low < high) { //当子序列中只有一个元素时结束递归
            int mid = (low + high) / 2; //划分子序列
            mergeSort(arr, low, mid); //对左侧子序列进行递归排序
            mergeSort(arr, mid + 1, high); //对右侧子序列进行递归排序
            merge(arr, low, mid, high); //合并
        }
    }

    private static void merge(int[] arr, int low, int mid, int high) {
        int[] temp = new int[arr.length]; //辅助数组
        int k = 0, i = low, j = mid + 1; //i左边序列和j右边序列起始索引,k是存放指针
        while (i <= mid && j <= high) {
            if (arr[i] <= arr[j]) {
                temp[k++] = arr[i++];
            } else {
                temp[k++] = arr[j++];
            }
        }
        //如果第一个序列未检测完，直接将后面所有元素加到合并的序列中
        while (i <= mid) {
            temp[k++] = arr[i++];
        }
        //同上
        while (j <= high) {
            temp[k++] = arr[j++];
        }
        //复制回原数组
        for (int t = 0; t < k; t++) {
            arr[low + t] = temp[t];
        }
    }

    public static void main(String[] args) {
        int[] arr = {1,28,3,21,11,7,6,18};
        mergeSort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }
}

The above is the detailed content of What is the principle of merge sort algorithm in Java and how to implement it. For more information, please follow other related articles on the PHP Chinese website!