
Data normalization is a very critical step in deep learning data preprocessing, which can unify dimensions and prevent small data from being swallowed up.
Normalization is to convert all data into [0,1] or [-1,1] The purpose is to cancel the order of magnitude difference between each dimension of data and avoid excessive network prediction errors due to large order of magnitude differences in input and output data.
For the convenience of subsequent data processing, normalization can avoid some unnecessary numerical problems.
In order to converge faster when the program is running
Unify the dimensions. The evaluation criteria for sample data are different, so it needs to be dimensionalized and the evaluation criteria unified. This is considered a requirement at the application level.
Avoid neuronal saturation. That is to say, when the activation of neurons is close to 0 or 1, in these areas, the gradient is almost 0, so that during the back propagation process, the local gradient will be close to 0, which is very unfavorable for network training.
Ensure that small values in the output data are not swallowed.
Linear normalization is also calledminimum- Maximum normalization; discrete normalization, is a linear transformation of the original data, mapping the data value to [0,1]. It is expressed as:
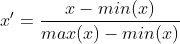
#Difference standardization retains the relationship existing in the original data and is the simplest method to eliminate the influence of dimensions and data value ranges. The code is implemented as follows:
def MaxMinNormalization(x,Max,Min):
x = (x - Min) / (Max - Min);
return xScope of application: more suitable for situations where numerical values are relatively concentrated
Disadvantages:
If max and min are unstable, it is very difficult to It is easy to make the normalized results unstable, making subsequent use effects also unstable. If the value range exceeds the current attribute [min, max], it will cause the system to report an error. Min and max need to be redetermined.
If a certain value in the value set is very large, then the normalized values will be close to 0 and will not differ much. (such as 1,1.2,1.3,1.4,1.5,1.6,10) this set of data.
Z-score standardization is also called standard deviation standardization, the mean of the processed data is 0 and the standard deviation is 1. The conversion formula is:
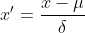
where 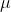 is the mean of the original data,
is the mean of the original data, 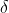 is the standard deviation of the original data, and is the most commonly used standardization formula
is the standard deviation of the original data, and is the most commonly used standardization formula
This method gives the mean and standard deviation of the original data to standardize the data. The processed data conforms to the standard normal distribution, that is, the mean is 0 and the standard deviation is 1. The key here is the composite standard normal distribution
The code is implemented as follows:
def Z_ScoreNormalization(x,mu,sigma):
x = (x - mu) / sigma;
return xThis method maps the attribute value to between [-1,1] by moving the decimal places of the attribute value. The number of decimal places moved depends on the maximum absolute value of the attribute value. The conversion formula is:
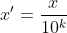
This method includes log, exponential, tangent
Scope of application: often It is used in scenarios where data analysis is relatively large. Some values are very large and some are very small. The original values are mapped.
In the past neural network training, only the input layer data was normalized. But there is no normalization processing in the middle layer. Although we have normalized the input data, after the input data has undergone matrix multiplication like  , its data distribution is likely to change greatly, and as the number of layers of the network continues to deepen. Data distribution will change more and more. Therefore, this normalization process in the middle layer of the neural network, which makes the training effect better, is called batch normalization (BN)
, its data distribution is likely to change greatly, and as the number of layers of the network continues to deepen. Data distribution will change more and more. Therefore, this normalization process in the middle layer of the neural network, which makes the training effect better, is called batch normalization (BN)
Reduces artificial selection of parameters
Reduces the requirement for learning rate, we can use a large learning rate in the initial state or use a smaller learning rate rate, the algorithm can also quickly train to converge.
Replaces the original data distribution and alleviates overfitting to a certain extent (preventing a certain sample from being frequently selected in each batch of training)
Reduce gradient disappearance, speed up convergence, and improve training accuracy.
Input: The output result of the previous layer X={x1,x2,...xm} ,Learning parameters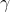 ,
,
Algorithm process:
1) Calculate the mean value of the output data of the previous layer:
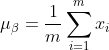
Among them, m is the size of this training sample batch.
2) Calculate the standard deviation of the output data of the previous layer:
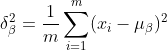
3) Normalize to get
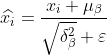
The  in the formula is a small value close to 0 that is added to avoid the denominator being 0.
in the formula is a small value close to 0 that is added to avoid the denominator being 0.
4) Reconstruction, reconstruct the data obtained after the above normalization process, and get:
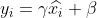
where 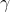 ,
, 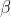 are learnable parameters.
are learnable parameters.
The above is the detailed content of What are the common normalization methods in Python?. For more information, please follow other related articles on the PHP Chinese website!




