How to implement Java stack and queue-javaTutorial-php.cn

1. Implement circular queue

[OJ link]

Circular queue is generally implemented through an array. We need to solve several problems.

(1) Array subscript implements loop

a, the subscript finally goes back (offset is less than array.length): index = (index offset) % array.length. To put it more simply, if the size of our array is 8 and the subscript reaches 7, then how to return to 0, we can achieve it by (index 1)%8.

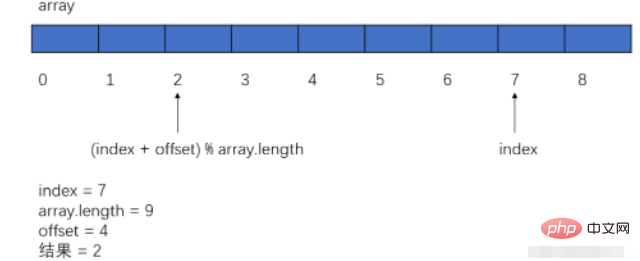
How to implement Java stack and queue

b. When the subscript is the first and then forward, we make a special judgment and set it to the array size minus one.

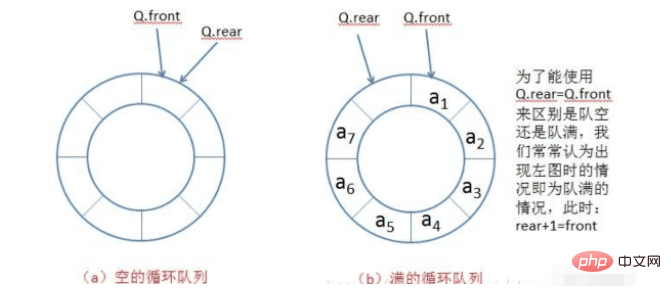
(2) Distinguish between full and empty queues

We can reserve a position for the array. If rear 1=front, it means that the queue is full; if rear=front, it means that the queue is null. In this case, we need to consider the queue size. When defining the array size, it needs to be one larger than the original one.

How to implement Java stack and queue

[The code is as follows]

class MyCircularQueue {
    public int front;
    public int rear;
    public int[] array;
 
    //构造方法
    public MyCircularQueue(int k) {
       //因为预留位置的缘故，数组的大小要定义为k+1
       this.array=new int[k+1];
    }
    //入队
    public boolean enQueue(int value) {
        if(isFull()){
            return false;
        }
        this.array[this.rear]=value;
        this.rear=(this.rear+1)%this.array.length;
        return true;
    }
    //出队
    public boolean deQueue() {
        if(isEmpty()){
            return false;
        }
        this.front=(this.front+1)%this.array.length;
        return true;
    }
    //获取队头
    public int Front() {
        if(isEmpty()){
            return -1;
        }
        return this.array[front];
    }
    //获取队尾
    public int Rear() {
        if(isEmpty()){
            return -1;
        }
        int index=-1;
        if(this.rear==0){
            index=this.array.length-1;
        }else{
            index=this.rear-1;
        }
        return this.array[index];
    }
    //判断是否为空
    public boolean isEmpty() {
        if(this.front==this.rear){
            return true;
        }
        return false;
    }
    //判断队列是否满
    public boolean isFull() {
        if((this.rear+1)%this.array.length==this.front){
            return true;
        }
        return false;
    }
}

Copy after login

2. Queue implementation stack

[OJ link]

Because of the stack First-in-last-out, first-in-first-out principle for queues. We need two queues to implement the stack. When both queues are empty, the stack is empty.

Push: It doesn’t matter the first time you push into the stack. Both queues are empty. Just choose a queue and put it into the queue. When you push into the stack later, there will definitely be one. The queue is not empty. Find a queue that is not empty and perform the enqueue operation.
Pop (pop): First, when the stack is empty, the pop operation cannot be performed; when the stack is not empty, there must be one queue that is empty (queue1), and one queue that is not Empty (queue2), pop size-1 elements in queue1 into queue2 (pay special attention not to put the function for finding the size of queue1 into the loop. When the queue is dequeued, its size changes), and finally The last element in queue1 is dequeued and is the return value.
Getting the top element of the stack (top): It’s almost the same as popping the stack, so I won’t go into details

[The code is as follows]

class MyStack {
    private Queue<Integer> queue1;
    private Queue<Integer> queue2;
 
    //构造方法
    public MyStack() {
        queue1=new LinkedList<>();
        queue2=new LinkedList<>();
    }
    //入栈
    public void push(int x) {
        if(!queue2.isEmpty()){
            queue2.offer(x);
        }else{
            queue1.offer(x);
        }
    }
    //出栈
    public int pop() {
        if(empty()){
            return -1;
        }
        if(queue1.isEmpty()){
            int size=queue2.size();
            for(int i=0;i<size-1;++i){
                int x=queue2.poll();
                queue1.offer(x);
            }
            return queue2.poll();
        }else{
            int size=queue1.size();
            for(int i=0;i<size-1;++i){
                int x=queue1.poll();
                queue2.offer(x);
            }
            return queue1.poll();
        }
    }
    //获取栈顶元素
    public int top() {
        if(empty()){
            return -1;
        }
        if(queue1.isEmpty()){
            int x=-1;
            int size=queue2.size();
            for(int i=0;i<size;++i){
                x=queue2.poll();
                queue1.offer(x);
            }
           return x;
        }else{
            int size=queue1.size();
            int x=-1;
            for(int i=0;i<size;++i){
                x=queue1.poll();
                queue2.offer(x);
            }
            return x;
        }
    }
    //判断栈是否为空
    public boolean empty() {
        if(queue1.isEmpty()&&queue2.isEmpty()){
            return true;
        }
        return false;
    }
}

Copy after login

3. Stack implementation queue

[OJ link]

Still the same as above, two stacks (stack1, stack2) are needed. Different from the implementation of stack queue, enqueueing can only operate on the same stack. If both stacks are empty, the queue is empty.

Enter the team (push): It is specified that stack1 is used to join the team. Each time you join the queue, just push stack1 into the stack.
Dequeue (pop): Requires stack2 to perform dequeue operation. If the queue is empty, the dequeue operation cannot be performed. When stack2 is empty, we need to pop all elements in stack1 into stack2, and then pop stack2. If stack2 is not empty, just pop stack2 directly.
Get the beginning element of the queue (peek): It is the same as the pop operation. In the end, you only need to get the top element of stack2.

[The code is as follows]

class MyQueue {
    private Stack<Integer> stack1;
    private Stack<Integer> stack2;
    //构造方法
    public MyQueue() {
        stack1=new Stack<>();
        stack2=new Stack<>();
    }
    //入队操作
    public void push(int x) {
        stack1.push(x);
    }
    //出队操作
    public int pop() {
        if(stack2.empty()){
            int size=stack1.size();
            for(int i=0;i<size;++i){
                int x=stack1.pop();
                stack2.push(x);
            }
        }
        return stack2.pop();
 
    }
    //获取队列开头的元素
    public int peek() {
        if(stack2.empty()){
            int size=stack1.size();
            for(int i=0;i<size;++i){
                int x=stack1.pop();
                stack2.push(x);
            }
        }
        return stack2.peek();
    }
    //判断队列是否为空
    public boolean empty() {
        if(stack1.empty()&&stack2.empty()){
            return true;
        }
        return false;
    }
}

Copy after login

4. Implement the minimum stack

[OJ link]

In fact, it is to be in O( 1) Find the smallest element of the stack within the time complexity. Two stacks are needed to implement it, and one stack is used for popping and pushing operations. Just make sure that no matter how you operate, the top element of the other stack is the smallest element of the current stack.

Two stacks stack1 and stack2, the operations of the station are all in stack1:

Pushing to the stack: If it is pushed to the stack for the first time, we need to put it too In stack2, when pushed onto the stack, the pushed element is compared with the top element of stack2. If it is smaller than the top element of stack2, it is put into stack2.
Pop: When popping stack1, compare it with the top element of stack2. If it is equal to the top element of stack2, pop stack2.

This ensures that the top element of stack2 is always the smallest element of stack1. Note: If two identical minimum elements are pushed into stack1, stack2 needs to be pushed into the stack.

[The code is as follows]

class MinStack {
    private Stack<Integer> stack1;
    private Stack<Integer> stack2;
    //构造方法
    public MinStack() {
        stack1=new Stack<>();
        stack2=new Stack<>();
    }
    //入栈
    public void push(int val) {
        stack1.push(val);
        if(stack2.empty()){
            stack2.push(val);
        }else{
            if(val<=stack2.peek()){
                stack2.push(val);
            }
        }
    }
    //出栈
    public void pop() {
        int x=stack1.pop();
        if(x==stack2.peek()){
            stack2.pop();
        }
    }
    //获取栈顶元素
    public int top() {
        return stack1.peek();
    }
    //获取栈的最小元素
    public int getMin() {
        return stack2.peek();
    }
}

Copy after login

The above is the detailed content of How to implement Java stack and queue. For more information, please follow other related articles on the PHP Chinese website!