How to use heap to solve Top-k problem in Java?
1. What is a heap?
Heap structure
Heap is actually a kind of binary tree, but ordinary binary trees store data in a chain structure, while heaps store data sequentially in arrays. So what kind of binary tree is suitable for sequential storage?
We assume that an ordinary binary tree can be stored in an array, then we can get the following structure:
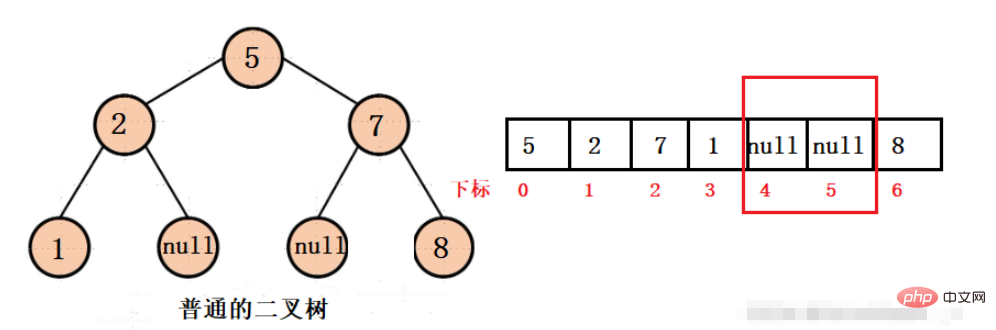
We can see that when there is space in the middle of the binary tree value, the storage space of the array will be wasted, so under what circumstances will the space not be wasted? That is a complete binary tree.
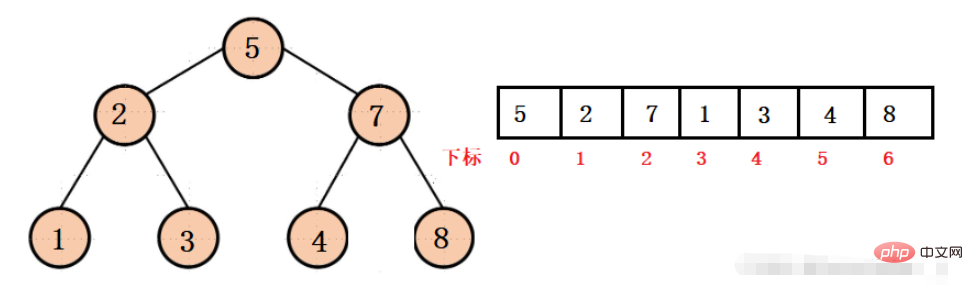
From the above structure, we cannot use the pointer of the chain structure to access the child node or parent node. We can only access it through the corresponding subscript, which is actually relatively simple.
For example, in the picture below:
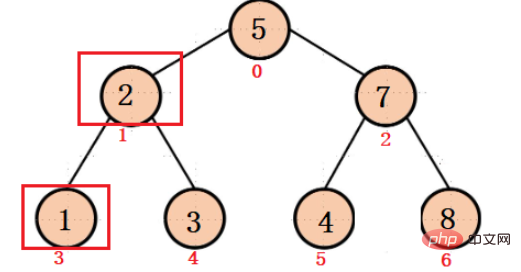
It is known that the subscript of node 2 is 1, then
The subscript of its left child is: 2 * 2 1 = 3
The subscript of his right child is: 2 * 2 2 = 4
On the contrary, it is known that the subscript of node 1 is 3 and the subscript of node 3 is 4, then
The parent node index of node 1 is: (3 - 1) / 2 = 1
The parent node index of node 3 is: (4 - 1) / 2 = 1
Big root heap VS small root heap
Big root heap (maximum heap)
The big root heap guarantees that the root node of each binary tree is larger than the left and right child nodes
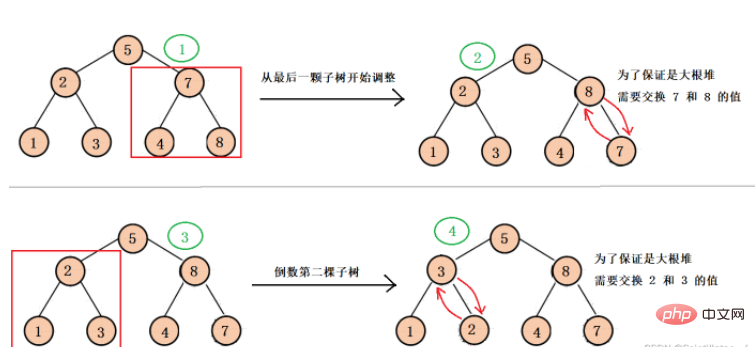
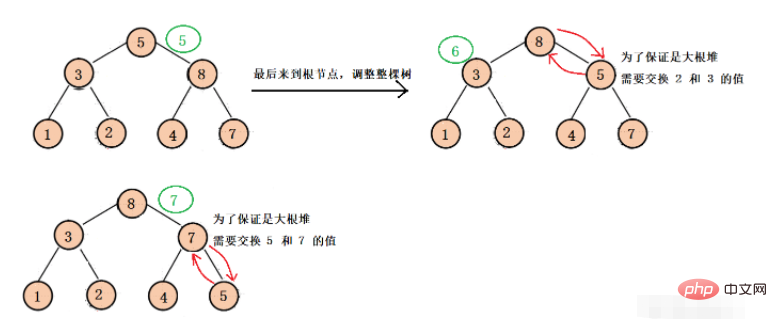
Start adjusting from the root node of the last subtree to the root node of each subtree, so that each subtree is adjusted downwards into a large root heap, and finally make the final adjustment downward to ensure that the entire binary tree is a large root heap ( This adjustment is mainly for the later heap sorting).
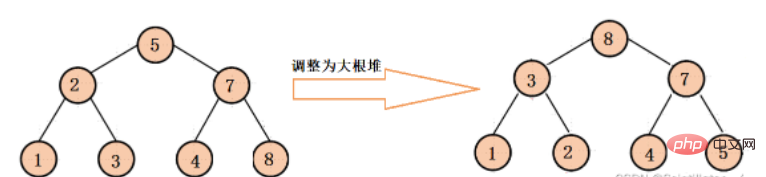
The specific adjustment process is as follows:
How to implement it with code?
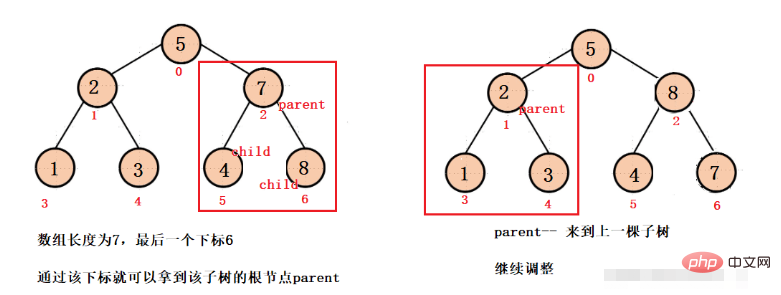
We first adjust from the last subtree, then we need to get the root node parent of the last subtree. We know that the last node subscript of the array is len - 1, and this node is the last subtree. For the left or right child of the tree, you can get the root node subscript (parent) based on the child subscript. Parent-- allows each subtree to be adjusted until it reaches the root node, and then adjust downward for the last time. , you can get a big root pile.
// 将数组变成大根堆结构
public void createHeap(int[] arr){
for (int i = 0; i < arr.length; i++) {
elem[i] = arr[i];// 放入elem[],假设不需要扩容
usedSize++;
}
// 得到根节点parent, parent--依次来到每颗子树的根节点,
for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {
// 依次向下搜索,使得每颗子树都变成大根堆
shiftDown(parent,usedSize);
}
}
// 向下搜索变成大根堆
public void shiftDown(int parent,int len){
int child = parent*2+1;// 拿到左孩子
while (child < len){
// 如果有右孩子,比较左右孩子大小,得到较大的值和父节点比较
if (child+1 < len && (elem[child] < elem[child+1])){
child++;
}
// 比较较大的孩子和父节点,看是否要交换
int max = elem[parent] >= elem[child] ? parent : child;
if (max == parent) break;// 如果不需要调整了,说明当前子树已经是大根堆了,直接 break
swap(elem,parent,child);
parent = child;// 继续向下检测,看是否要调整
child = parent*2+1;
}
}
public void swap(int[] arr,int i,int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
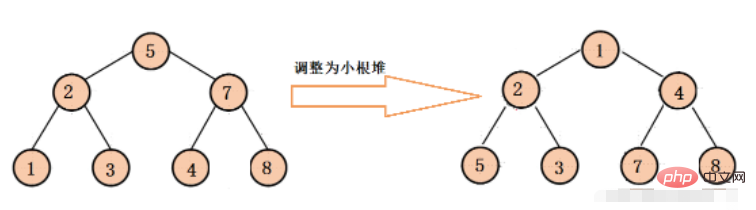
}Small root heap (minimum heap)
The small root heap ensures that the root node of each binary tree is smaller than the left and right child nodes
The adjustment process is the same as above.
Priority Queue (PriorityQueue)
In java, a heap data structure (PriorityQueue) is provided, also called a priority queue. When we When creating such an object, we get a small root heap with no added data. We can add or delete elements to it. Every time an element is deleted or added to it, the system will make an overall adjustment and adjust it to the small root heap again. heap.
// 默认得到一个小根堆
PriorityQueue<Integer> smallHeap = new PriorityQueue<>();
smallHeap.offer(23);
smallHeap.offer(2);
smallHeap.offer(11);
System.out.println(smallHeap.poll());// 弹出2,剩余最小的元素就是11,会被调整到堆顶,下一次弹出
System.out.println(smallHeap.poll());// 弹出11
// 如果需要得到大根堆,在里面传一个比较器
PriorityQueue<Integer> BigHeap = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});2. Ideas for solving top-k problems
Example: There are a bunch of elements and you are asked to find the first three smallest elements.
Idea 1: Sort the array from small to large and get the first 3 elements of the array. However, it can be found that the time complexity of this method is too high and is not advisable.
Idea 2: Put all the elements into a heap structure, and then pop up three elements. Each pop-up element is the smallest in the current heap, then the three pop-up elements are the first three smallest elements. .
This idea can be done, but assuming I have 1,000,000 elements and only pop up the first three smallest elements, then a heap of size 1,000,000 will be used. The space complexity of doing this is too high, so this method is not recommended.
Three ideas:
We need to get the three smallest elements, then build a heap with a size of 3. Assume that the current heap structure is filled with exactly 3 elements, then this The three elements are the current three smallest elements. Assuming that the fourth element is one of the elements we want, then at least one of the first three elements is not what we want, and it needs to be popped. So who should pop up?
What we want to get is the first three smallest elements, so the largest element in the current heap structure must not be what we want, so here we build a large root heap. Pop the element and then put in the fourth element until the entire array is traversed.
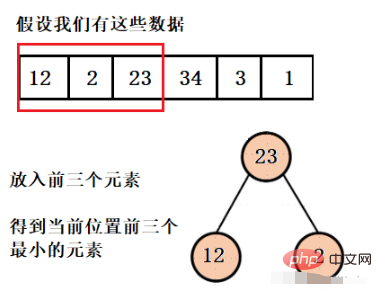
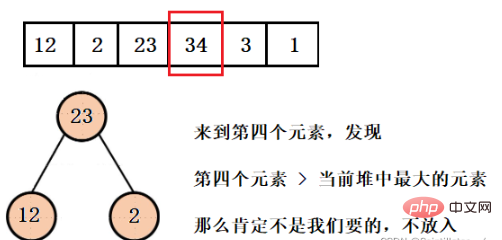
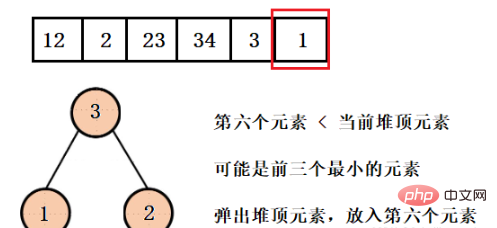
这样我们就得到了只含有前三个最小元素的堆,并且可以看到堆的大小一直都是3,而不是有多少数据就建多大的堆,然后再依次弹出元素就行了。
// 找前 k个最小的元素
public static int[] topK(int[] arr,int k){
// 创建一个大小为 k的大根堆
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k,new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
for (int i = 0; i < arr.length; i++) {
if (i < k){
// 放入前 k 个元素
maxHeap.offer(arr[i]);
}else{
// 从第 k+1个元素开始进行判断是否要入堆
if (maxHeap.peek() > arr[i]){
maxHeap.poll();
maxHeap.offer(arr[i]);
}
}
}
int[] ret = new int[k];
for (int i = 0; i < k; i++) {
ret[i] = maxHeap.poll();
}
return ret;
}The above is the detailed content of How to use heap to solve Top-k problem in Java?. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Square Root in Java
Aug 30, 2024 pm 04:26 PM
Square Root in Java
Aug 30, 2024 pm 04:26 PM
Guide to Square Root in Java. Here we discuss how Square Root works in Java with example and its code implementation respectively.
 Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Perfect Number in Java. Here we discuss the Definition, How to check Perfect number in Java?, examples with code implementation.
 Random Number Generator in Java
Aug 30, 2024 pm 04:27 PM
Random Number Generator in Java
Aug 30, 2024 pm 04:27 PM
Guide to Random Number Generator in Java. Here we discuss Functions in Java with examples and two different Generators with ther examples.
 Armstrong Number in Java
Aug 30, 2024 pm 04:26 PM
Armstrong Number in Java
Aug 30, 2024 pm 04:26 PM
Guide to the Armstrong Number in Java. Here we discuss an introduction to Armstrong's number in java along with some of the code.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Guide to Weka in Java. Here we discuss the Introduction, how to use weka java, the type of platform, and advantages with examples.
 Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Smith Number in Java. Here we discuss the Definition, How to check smith number in Java? example with code implementation.
 Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
In this article, we have kept the most asked Java Spring Interview Questions with their detailed answers. So that you can crack the interview.
 Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Java 8 introduces the Stream API, providing a powerful and expressive way to process data collections. However, a common question when using Stream is: How to break or return from a forEach operation? Traditional loops allow for early interruption or return, but Stream's forEach method does not directly support this method. This article will explain the reasons and explore alternative methods for implementing premature termination in Stream processing systems. Further reading: Java Stream API improvements Understand Stream forEach The forEach method is a terminal operation that performs one operation on each element in the Stream. Its design intention is






