What are the basic knowledge and concepts of binary trees in Java?
1. Tree structure
1.1 Concept
Tree is a non-linear data structure, which is composed of n (n> ;=0) finite nodes form a set with hierarchical relationships. It is called a tree because it looks like an upside-down tree, that is to say, it has the roots facing up and the leaves facing down.
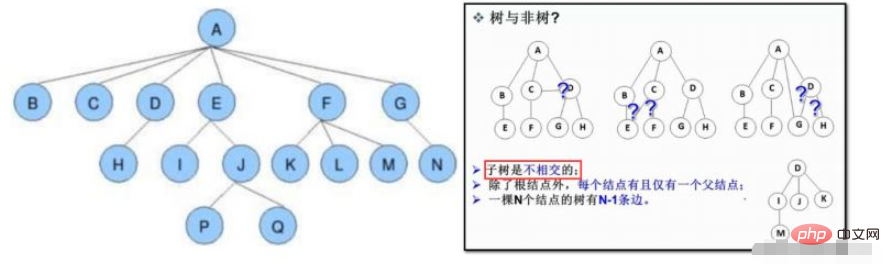
1.2 Concept (Important)
a. The degree of a node: the number of subtrees of the node; as shown above: the degree of A is 6, J The degree of is 2
b. The degree of the tree: In this tree, the degree of the largest node is the degree of the number; as shown in the figure above: the degree of the tree is 6
c. The leaf node ( Terminal node): A node with degree 0 (node without subtree)
d. Parent node/parent node: As shown above: D is the parent node of H
Child node/child Node: As shown in the picture above: H is the child node of D
e. Root node: A node without parents; as shown in the picture above: A
f. Node level: Starting from the root, the root is Level 1, the child node of the root is level 2, and so on;
g. The height or depth of the tree: the maximum level of nodes in the tree; As shown above: the height of the tree is 4
2. Binary tree (key point)
2.1 Concept
Each node has at most two subtrees, degree
2.2 Basic form of binary tree
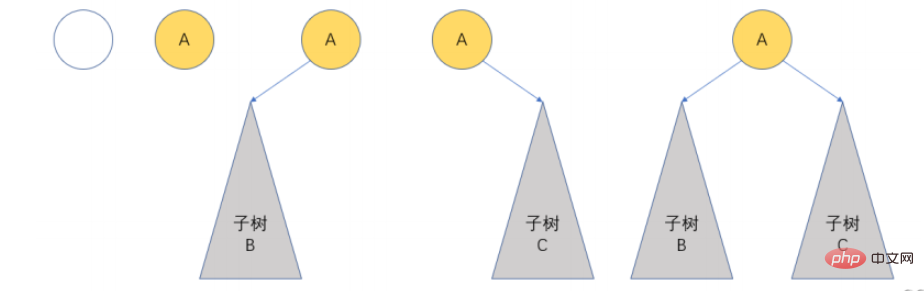
2.3 Two special binary trees
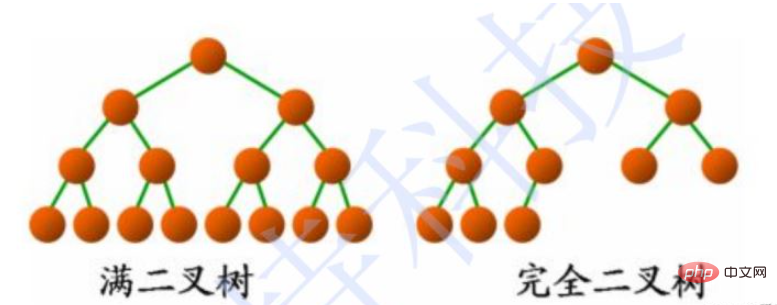
a. Full binary tree: non-cotyledon degree is 2
b. Complete binary tree: a full binary tree is missing the "lower right corner"
2.4 Properties of binary trees
a. Full binary tree
1. Height is K, then there are 2^k-1 nodes
2. The level is K, then the layer has 2^(k-1) nodes
3. Number of edges = nodes Number - 1
4. There are n0 with degree 0, and n2 with degree 2, then n0 = n2 1
b. Complete binary tree
1. If there is a right child, there must be a left child
2. There can only be one node with degree 1
2.5 Storage of binary trees
The storage structure of binary trees is divided into For: sequential storage and linked list-like storage.
Sequential storage: only complete binary trees can be stored
Chained storage: ordinary binary trees
This time we show chained storage
The chained storage of binary trees is Referenced by nodes one by one, common representation methods include binary and trifurcated representations,
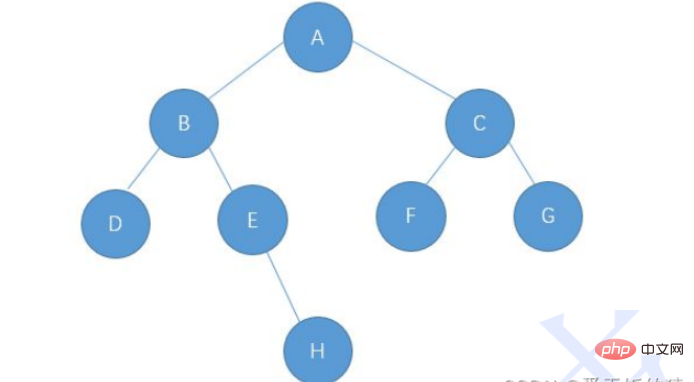
Take this picture as an example, the details are as follows:
// 孩子表示法
private static class TreeNode{
char val;
TreeNode left;
TreeNode right;
public TreeNode(char val) {
this.val = val;
}
}Initialization:
public static TreeNode build(){
TreeNode nodeA=new TreeNode('A');
TreeNode nodeB=new TreeNode('B');
TreeNode nodeC=new TreeNode('C');
TreeNode nodeD=new TreeNode('D');
TreeNode nodeE=new TreeNode('E');
TreeNode nodeF=new TreeNode('F');
TreeNode nodeG=new TreeNode('G');
TreeNode nodeH=new TreeNode('H');
nodeA.left=nodeB;
nodeA.right=nodeC;
nodeB.left=nodeD;
nodeB.right=nodeE;
nodeE.right=nodeH;
nodeC.left=nodeF;
nodeC.right=nodeG;
return nodeA;
}2.6 Basic operations of binary trees
2.6.1 Binary tree traversal (recursive)
1. NLR: Preorder Traversal (also known as Preorder Traversal) Order traversal)—— Visit the root node---> the left subtree of the root---> the right subtree of the root.
//先序遍历 : 根左右
public static void preOrder(TreeNode root){
if(root==null){
return;
}
System.out.print(root.val+" ");
preOrder(root.left);
preOrder(root.right);
}2. LNR: Inorder Traversal (Inorder Traversal)—— The left subtree of the root ---> The root node ---> The right subtree of the root.
//中序遍历
public static void inOrder(TreeNode root){
if(root==null){
return;
}
preOrder(root.left);
System.out.print(root.val+" ");
preOrder(root.right);
}3. LRN: Postorder Traversal - left subtree of the root ---> right subtree of the root ---> root node.
//后序遍历
public static void postOrder(TreeNode root){
if(root==null){
return;
}
preOrder(root.left);
preOrder(root.right);
System.out.print(root.val+" ");
}2.6.2 Binary tree traversal (iteration)
1. Preorder traversal
//方法2(迭代)
//先序遍历 (迭代)
public static void preOrderNonRecursion(TreeNode root){
if(root==null){
return ;
}
Deque<TreeNode> stack=new LinkedList<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode cur=stack.pop();
System.out.print(cur.val+" ");
if(cur.right!=null){
stack.push(cur.right);
}
if(cur.left!=null){
stack.push(cur.left);
}
}
}2. Inorder traversal
//方法2(迭代)
//中序遍历 (迭代)
public static void inorderTraversalNonRecursion(TreeNode root) {
if(root==null){
return ;
}
Deque<TreeNode> stack=new LinkedList<>();
// 当前走到的节点
TreeNode cur=root;
while (!stack.isEmpty() || cur!=null){
// 不管三七二十一,先一路向左走到根儿~
while (cur!=null){
stack.push(cur);
cur=cur.left;
}
// 此时cur为空,说明走到了null,此时栈顶就存放了左树为空的节点
cur=stack.pop();
System.out.print(cur.val+" ");
// 继续访问右子树
cur=cur.right;
}
}3.Postorder traversal Traversing
//方法2(迭代)
//后序遍历 (迭代)
public static void postOrderNonRecursion(TreeNode root){
if(root==null){
return;
}
Deque<TreeNode> stack=new LinkedList<>();
TreeNode cur=root;
TreeNode prev=null;
while (!stack.isEmpty() || cur!=null){
while (cur!=null){
stack.push(cur);
cur=cur.left;
}
cur=stack.pop();
if(cur.right==null || prev==cur.right){
System.out.print(cur.val+" ");
prev=cur;
cur=null;
}else {
stack.push(cur);
cur=cur.right;
}
}
}2.6.3 Basic operations of binary trees
1. Find the number of nodes (recursion & iteration)
//方法1(递归)
//传入一颗二叉树的根节点,就能统计出当前二叉树中一共有多少个节点,返回节点数
//此时的访问就不再是输出节点值,而是计数器 + 1操作
public static int getNodes(TreeNode root){
if(root==null){
return 0;
}
return 1+getNodes(root.left)+getNodes(root.right);
}
//方法2(迭代)
//使用层序遍历来统计当前树中的节点个数
public static int getNodesNoRecursion(TreeNode root){
if(root==null){
return 0;
}
int size=0;
Deque<TreeNode> queue=new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
size++;
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
return size;
}2. Find the number of leaf nodes (recursion & iteration)
//方法1(递归)
//传入一颗二叉树的根节点,就能统计出当前二叉树的叶子结点个数
public static int getLeafNodes(TreeNode root){
if(root==null){
return 0;
}
if(root.left==null && root.right==null){
return 1;
}
return getLeafNodes(root.left)+getLeafNodes(root.right);
}
//方法2(迭代)
//使用层序遍历来统计叶子结点的个数
public static int getLeafNodesNoRecursion(TreeNode root){
if(root==null){
return 0;
}
int size=0;
Deque<TreeNode> queue=new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
TreeNode cur=queue.poll();
if(cur.left==null && cur.right==null){
size++;
}
if(cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
}
return size;
}3. Find the number of nodes in the kth layer
//求出以root为根节点的二叉树第k层的节点个数
public static int getKLevelNodes(TreeNode root,int k){
if(root==null || k<=0){
return 0;
}
if(k==1){
return 1;
}
return getKLevelNodes(root.left,k-1)+getKLevelNodes(root.right,k-1);
}4. Find the height of the tree
//传入一个以root为根节点的二叉树,就能求出该树的高度
public static int height(TreeNode root){
if(root==null){
return 0;
}
return 1+ Math.max(height(root.left),height(root.right));
}5. Determine whether there is a value in the binary tree number. The node of value
//判断当前以root为根节点的二叉树中是否包含指定元素val,
//若存在返回true,不存在返回false
public static boolean contains(TreeNode root,char value){
if(root==null){
return false;
}
if(root.val==value){
return true;
}
return contains(root.left,value) || contains(root.right,value);
}2.7 Level-order traversal of binary tree
//层序遍历
public static void levelOrder(TreeNode root) {
if(root==null){
return ;
}
// 借助队列来实现遍历过程
Deque<TreeNode> queue =new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
int size=queue.size();
for (int i = 0; i < size; i++) {
TreeNode cur=queue.poll();
System.out.print(cur.val+" ");
if(cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
}
}
}The above is the detailed content of What are the basic knowledge and concepts of binary trees in Java?. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1393
1393
 52
52
 1205
1205
 24
24
 Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Perfect Number in Java. Here we discuss the Definition, How to check Perfect number in Java?, examples with code implementation.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Guide to Weka in Java. Here we discuss the Introduction, how to use weka java, the type of platform, and advantages with examples.
 Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Smith Number in Java. Here we discuss the Definition, How to check smith number in Java? example with code implementation.
 Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
In this article, we have kept the most asked Java Spring Interview Questions with their detailed answers. So that you can crack the interview.
 Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Java 8 introduces the Stream API, providing a powerful and expressive way to process data collections. However, a common question when using Stream is: How to break or return from a forEach operation? Traditional loops allow for early interruption or return, but Stream's forEach method does not directly support this method. This article will explain the reasons and explore alternative methods for implementing premature termination in Stream processing systems. Further reading: Java Stream API improvements Understand Stream forEach The forEach method is a terminal operation that performs one operation on each element in the Stream. Its design intention is
 TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
Guide to TimeStamp to Date in Java. Here we also discuss the introduction and how to convert timestamp to date in java along with examples.
 Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Capsules are three-dimensional geometric figures, composed of a cylinder and a hemisphere at both ends. The volume of the capsule can be calculated by adding the volume of the cylinder and the volume of the hemisphere at both ends. This tutorial will discuss how to calculate the volume of a given capsule in Java using different methods. Capsule volume formula The formula for capsule volume is as follows: Capsule volume = Cylindrical volume Volume Two hemisphere volume in, r: The radius of the hemisphere. h: The height of the cylinder (excluding the hemisphere). Example 1 enter Radius = 5 units Height = 10 units Output Volume = 1570.8 cubic units explain Calculate volume using formula: Volume = π × r2 × h (4
 Create the Future: Java Programming for Absolute Beginners
Oct 13, 2024 pm 01:32 PM
Create the Future: Java Programming for Absolute Beginners
Oct 13, 2024 pm 01:32 PM
Java is a popular programming language that can be learned by both beginners and experienced developers. This tutorial starts with basic concepts and progresses through advanced topics. After installing the Java Development Kit, you can practice programming by creating a simple "Hello, World!" program. After you understand the code, use the command prompt to compile and run the program, and "Hello, World!" will be output on the console. Learning Java starts your programming journey, and as your mastery deepens, you can create more complex applications.




