Steps and implementation of Timsort sorting algorithm in Java
Background
Timsort is a hybrid and stable sorting algorithm. Simply put, it is a mixture of merge sort and binary insertion sort algorithms. It is known as the world's best sorting algorithm. The best sorting algorithm. Timsort has always been Python's standard sorting algorithm. The Timsort API was added after Java SE 7. We can see from Arrays.sort that it is already the default sorting algorithm for non-primitive type arrays. So whether it is advanced programming learning or an interview, it is more important to understand Timsort.
// List sort()
default void sort(Comparator<? super E> c) {
Object[] a = this.toArray();
//数组排序
Arrays.sort(a, (Comparator) c);
...
}
// Arrays.sort
public static <T> void sort(T[] a, Comparator<? super T> c) {
if (c == null) {
sort(a);
} else {
// 废弃版本
if (LegacyMergeSort.userRequested)
legacyMergeSort(a, c);
else
TimSort.sort(a, 0, a.length, c, null, 0, 0);
}
}
public static void sort(Object[] a) {
if (LegacyMergeSort.userRequested)
legacyMergeSort(a);
else
ComparableTimSort.sort(a, 0, a.length, null, 0, 0);
}Prerequisite knowledge
To understand Timsort, you need to review the following knowledge first.
Exponential Search
Exponential search, also known as doubling search, is an algorithm created for searching for elements in large arrays. It is a two-step process. First, the algorithm tries to find the range (L,R) in which the target element exists, and then uses binary search within this range to find the exact location of the target. The time complexity is O(lgn). This search algorithm is effective in large ordered arrays.
Binary Insertion Sort
The insertion sort algorithm is very simple. The general process is to start from the second element and move forward and exchange elements until the appropriate position is found.

The optimal time complexity of insertion sort is also O(n). We can use binary search to reduce the number of comparisons of elements during insertion and reduce the time complexity to logn. . However, note that binary search insertion sort still requires moving the same number of elements, but the time consumption of copying the array is lower than that of a one-by-one swap operation.
Features: The main advantage of binary insertion sort is that the sorting efficiency is very high in small data set scenarios.
public static int[] sort(int[] arr) throws Exception {
// 开始遍历第一个元素后的所有元素
for (int i = 1; i < arr.length; i++) {
// 需要插入的元素
int tmp = arr[i];
// 从已排序最后一个元素开始,如果当前元素比插入元素大,就往后移动
int j = i;
while (j > 0 && tmp < arr[j - 1]) {
arr[j] = arr[j - 1];
j--;
}
// 将元素插入
if (j != i) {
arr[j] = tmp;
}
}
return arr;
}
public static int[] binarySort(int[] arr) throws Exception {
for (int i = 1; i < arr.length; i++) {
// 需要插入的元素
int tmp = arr[i];
// 通过二分查找直接找到插入位置
int j = Math.abs(Arrays.binarySearch(arr, 0, i, tmp) + 1);
// 找到插入位置后,通过数组复制向后移动,腾出元素位置
System.arraycopy(arr, j, arr, j + 1, i - j);
// 将元素插入
arr[j] = tmp;
}
return arr;
}Merge sort
Merge sort is an algorithm that utilizes the divide-and-conquer strategy and contains two main operations: Split and Merge . The general process is to recursively divide the array into two halves until it can no longer be divided (that is, the array is empty or has only one element left), and then merge and sort. Simply put, the merge operation is to continuously take two smaller sorted arrays and combine them into a larger array.
Features: Merge sort is a sorting algorithm mainly designed for large data set scenarios.

public static void mergeSortRecursive(int[] arr, int[] result, int start, int end) {
// 跳出递归
if (start >= end) {
return;
}
// 待分割的数组长度
int len = end - start;
int mid = (len >> 1) + start;
int left = start; // 左子数组开始索引
int right = mid + 1; // 右子数组开始索引
// 递归切割左子数组,直到只有一个元素
mergeSortRecursive(arr, result, left, mid);
// 递归切割右子数组,直到只有一个元素
mergeSortRecursive(arr, result, right, end);
int k = start;
while (left <= mid && right <= end) {
result[k++] = arr[left] < arr[right] ? arr[left++] : arr[right++];
}
while (left <= mid) {
result[k++] = arr[left++];
}
while (right <= end) {
result[k++] = arr[right++];
}
for (k = start; k <= end; k++) {
arr[k] = result[k];
}
}
public static int[] merge_sort(int[] arr) {
int len = arr.length;
int[] result = new int[len];
mergeSortRecursive(arr, result, 0, len - 1);
return arr;
}Timsort execution process
The general process of the algorithm, if the array length is less than the specified threshold (MIN_MERGE), use it directly The binary insertion algorithm completes the sorting, otherwise perform the following steps:
Start from the left side of the array and execute Ascending order to obtain a subsequence.
Put this subsequence into the running stack and wait for to execute the merge.
Check the subsequence in the running stack, and execute the merge if merging conditions are met.
Repeat the first step and perform the next ascending run.
Ascending order operation
Ascending order operation is the process of finding a continuous increasing (ascending order) or decreasing (descending order) subsequence from the array. If the subsequence If the sequence is in descending order, reverse it to ascending order. This process can also be referred to as run. For example, in the array [2,3,6,4,9,30], you can find three subsequences, [2,3,6], [4,9], [30], or 3 run.
Several key thresholds
MIN_MERGE
This is a constant value, which can be simply understood as the minimum threshold for merging. If the entire array length If it is smaller than it, there is no need to perform such complicated sorting, just binary insertion. In Tim Peter's C implementation, it is 64, but in actual experience, setting it to 32 works better, so the value in java is 32.
To ensure stability when reversing descending order, the same elements will not be reversed.
minrun
When merging sequences, if the number run is equal to or slightly less than the power of 2, merge The highest efficiency; if it is slightly larger than a power of 2, the efficiency will be significantly reduced. Therefore, in order to improve the efficiency of merging, it is necessary to control the length of each run as much as possible. By defining a minrun to represent the minimum length of each run, if the length is too short , just use binary insertion sort to insert the elements after run into the previous run.
Generally, before executing the sorting algorithm, this minrun will be calculated first (it adjusts itself according to the characteristics of the data). minrun will select a number from 32 to 64, so the size of the data divided by minrun is equal to Or slightly less than a power of 2. For example, if the length is 65, then the value of minrun is 33; if the length is 165, the value of minrun is 42.
看下 Java 里面的实现,如果数据长度(n) < MIN_MERGE,则返回数据长度。如果数据长度恰好是 2 的幂次方,则返回MIN_MERGE/2
也就是16,否则返回一个MIN_MERGE/2 <= k <= MIN_MERGE范围的值k,这样可以使的 n/k 接近但严格小于 2 的幂次方。
private static int minRunLength(int n) {
assert n >= 0;
int r = 0; // 如果低位任何一位是1,就会变成1
while (n >= MIN_MERGE) {
r |= (n & 1);
n >>= 1;
}
return n + r;
}MIN_GALLOP
MIN_GALLOP 是为了优化合并的过程设定的一个阈值,控制进入 GALLOP 模式中, GALLOP 模式放在后面讲。
下面是 Timsort 执行流程图
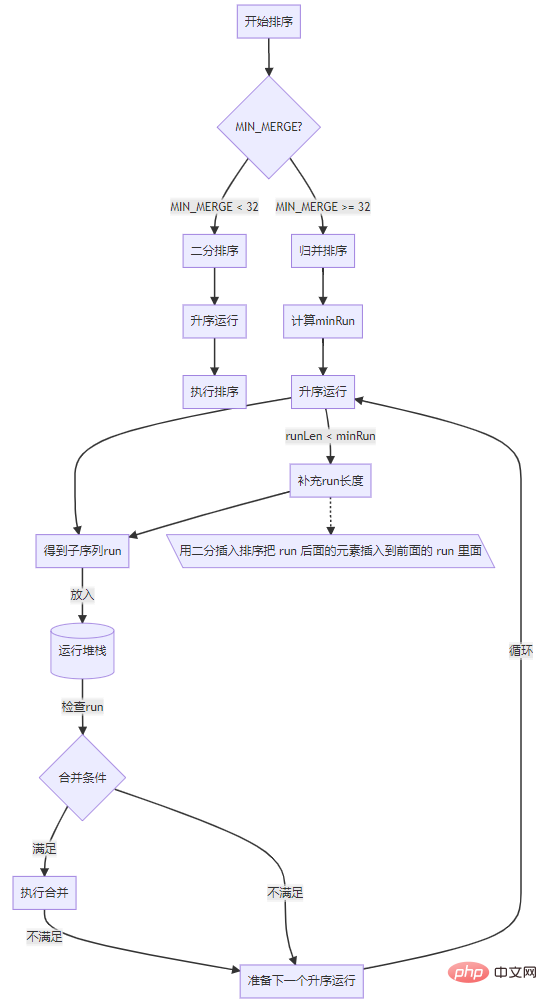
运行合并
当栈里面的 run 满足合并条件时,它就将栈里面相邻的两个run 进行合并。
合并条件
Timsort 为了执行平衡合并(让合并的 run 大小尽可能相同),制定了一个合并规则,对于在栈顶的三个run,分别用X、Y 和 Z 表示他们的长度,其中 X 在栈顶,它们必须始终维持一下的两个规则:
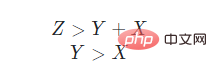
一旦有其中的一个条件不被满足,则将 Y 与 X 或 Z 中的较小者合并生成新的 run,并再次检查栈顶是否仍然满足条件。如果不满足则会继续进行合并,直至栈顶的三个元素都满足这两个条件,如果只剩两个run,则满足 Y > X 即可。
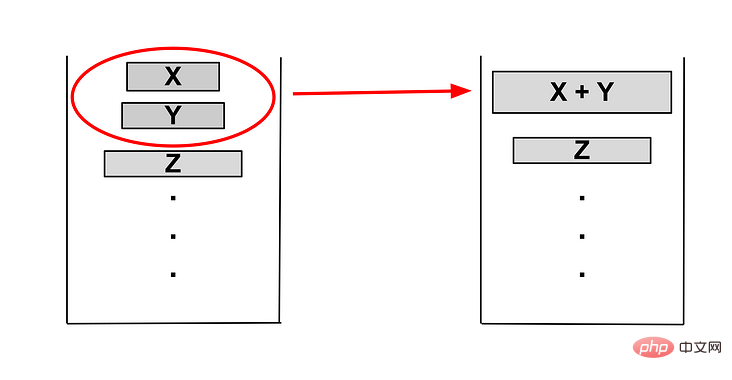
如下下图例子
当 Z <= Y+X ,将 X+Y 合并,此时只剩下两个run。
检测 Y < X ,执行合并,此时只剩下 X,则退出合并检测。
我们看下 Java 里面的合并实现
private void mergeCollapse() {
// 当存在两个以上run执行合并检查
while (stackSize > 1) {
// 表示 Y
int n = stackSize - 2;
// Z <= Y + X
if (n > 0 && runLen[n-1] <= runLen[n] + runLen[n+1]) {
// 如果 Z < X 合并Z+Y ,否则合并X+Y
if (runLen[n - 1] < runLen[n + 1])
n--;
// 合并相邻的两个run,也就是runLen[n] 和 runLen[n+1]
mergeAt(n);
} else if (runLen[n] <= runLen[n + 1]) {
// Y <= X 合并 Y+X
mergeAt(n);
} else {
// 满足两个条件,跳出循环
break;
}
}
}合并内存开销
原始归并排序空间复杂度是 O(n)也就是数据大小。为了实现中间项,Timsort 进行了一次归并排序,时间开销和空间开销都比 O(n)小。
优化是为了尽可能减少数据移动,占用更少的临时内存,先找出需要移动的元素,然后将较小序列复制到临时内存,在按最终顺序排序并填充到组合序列中。
比如我们需要合并 X [1, 2, 3, 6, 10] 和 Y [4, 5, 7, 9, 12, 14, 17],X 中最大元素是10,我们可以通过二分查找确定,它需要插入到 Y 的第 5个位置才能保证顺序,而 Y 中最小元素是4,它需要插入到 X 中的第4个位置才能保证顺序,那么就知道了[1, 2, 3] 和 [12, 14, 17] 不需要移动,我们只需要移动 [6, 10] 和 [4, 5, 7, 9],然后只需要分配一个大小为 2 临时存储就可以了。
合并优化
在归并排序算法中合并两个数组需要一一比较每个元素,为了优化合并的过程,设定了一个阈值 MIN_GALLOP,当B中元素向A合并时,如果A中连续 MIN_GALLOP 个元素比B中某一个元素要小,那么就进入GALLOP模式。
根据基准测试,比如当A中连续7个以上元素比B中某一元素小时切入该模式效果才好,所以初始值为7。
当进入GALLOP模式后,搜索算法变为指数搜索,分为两个步骤,比如想确定 A 中元素x在 B 中确定的位置
首先在 B 中找到合适的索引区间(2k−1,2k+1−1) 使得 x 元素在这个范围内;
然后在第一步找到的范围内通过二分搜索来找到对应的位置。
只有当一次运行的初始元素不是另一次运行的前七个元素之一时,驰骋才是有益的。这意味着初始阈值为 7。
The above is the detailed content of Steps and implementation of Timsort sorting algorithm in Java. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Square Root in Java
Aug 30, 2024 pm 04:26 PM
Square Root in Java
Aug 30, 2024 pm 04:26 PM
Guide to Square Root in Java. Here we discuss how Square Root works in Java with example and its code implementation respectively.
 Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Perfect Number in Java. Here we discuss the Definition, How to check Perfect number in Java?, examples with code implementation.
 Random Number Generator in Java
Aug 30, 2024 pm 04:27 PM
Random Number Generator in Java
Aug 30, 2024 pm 04:27 PM
Guide to Random Number Generator in Java. Here we discuss Functions in Java with examples and two different Generators with ther examples.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Guide to Weka in Java. Here we discuss the Introduction, how to use weka java, the type of platform, and advantages with examples.
 Armstrong Number in Java
Aug 30, 2024 pm 04:26 PM
Armstrong Number in Java
Aug 30, 2024 pm 04:26 PM
Guide to the Armstrong Number in Java. Here we discuss an introduction to Armstrong's number in java along with some of the code.
 Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Smith Number in Java. Here we discuss the Definition, How to check smith number in Java? example with code implementation.
 Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
In this article, we have kept the most asked Java Spring Interview Questions with their detailed answers. So that you can crack the interview.
 Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Java 8 introduces the Stream API, providing a powerful and expressive way to process data collections. However, a common question when using Stream is: How to break or return from a forEach operation? Traditional loops allow for early interruption or return, but Stream's forEach method does not directly support this method. This article will explain the reasons and explore alternative methods for implementing premature termination in Stream processing systems. Further reading: Java Stream API improvements Understand Stream forEach The forEach method is a terminal operation that performs one operation on each element in the Stream. Its design intention is






