
Recursion is: the process of calling a method by itself.
There are two prerequisites for using recursion:
1. There is an approach and termination condition.
2. Call yourself.
How to implement recursion?
The most important way is: to implement recursion, you need to derive a recursive formula.
The way to think about recursion: think laterally and think according to the recursive formula.
Code execution: vertical execution.
First look at the following code:
public class TestDemo {
public static void func(){
func(); //自己调用自己本身
}
public static void main(String[] args) {
func();
}
}The code above is a simple recursion.
Let’s take a look at the running results of this code.
Drawing explanation:
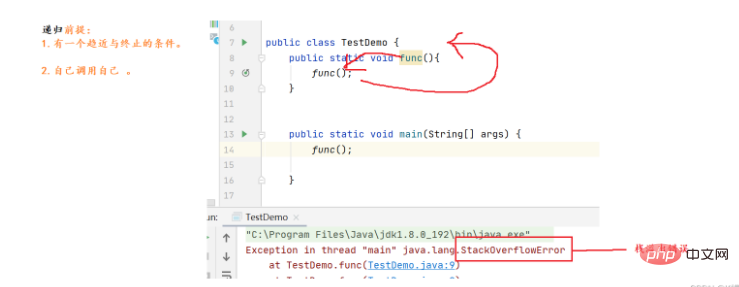
For the recursion in the above picture, there is no A condition that tends to terminate, so this function will recurse endlessly. Every time you recurse, memory must be allocated on the stack. If you keep allocating memory on the stack, the stack will eventually overflow.
Veterans, please remember: Once there is a problem with the recursion you write, if the boundary is not found correctly, a

will be reported. If it is reported, This error must be because your termination condition is wrong, or the termination condition is not written, which causes your recursion to be too deep, and eventually the stack overflows.
If we want the above code to be correct, we need to add a termination condition to it.
The correct code is as follows:
public class TestDemo {
public static void func(int n){
if(n == 1) return;
func(n -1);
}
public static void main(String[] args) {
func(3);
}
}The following will give you a deeper understanding of recursion through simple examples
Example: Recursion Method to find the factorial of n Drawing analysis:

Implementation code:
public class TestDemo {
public static int fac(int n){
if(n == 1) {
return 1;
}
int tmp = n * fac(n - 1);
return tmp;
}
public static void main(String[] args) {
System.out.println(fac(5));
}
}Code drawing explanation:
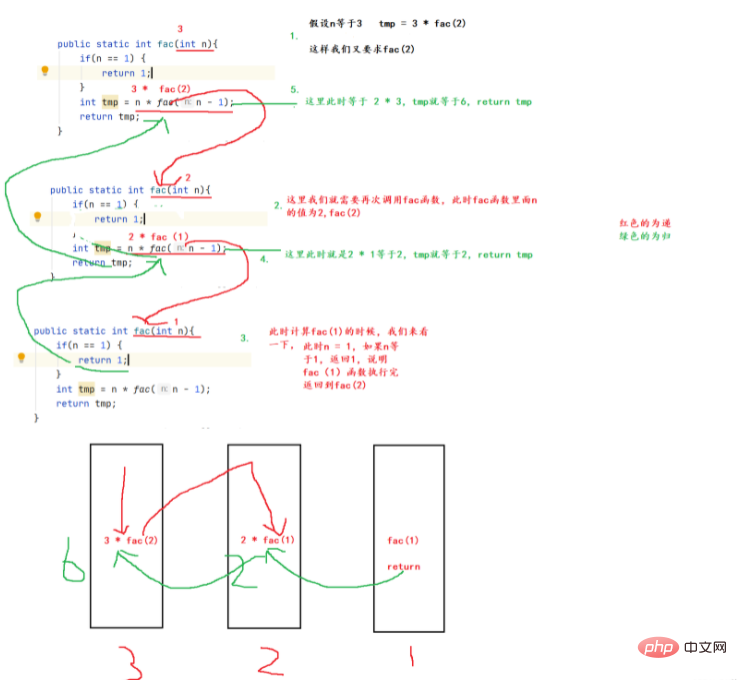
Example question: Find the sum of n
Drawing analysis:

Implementation code:
第一种写法:
public class TestDemo {
public static int sumAdd(int n){
if(n == 1) {
return 1;
}
int tmp = n + sumAdd(n - 1);
return tmp;
}
public static void main(String[] args) {
System.out.println(sumAdd(3));
}
}
第二种写法:
public class TestDemo {
public static int sumAdd(int n){
if(n == 1) {
return 1;
}
return n + sumAdd(n -1);
}
public static void main(String[] args) {
System.out.println(sumAdd(3));
}
}Example question: Recursive implementation prints each item in order One-digit number
Drawing analysis:
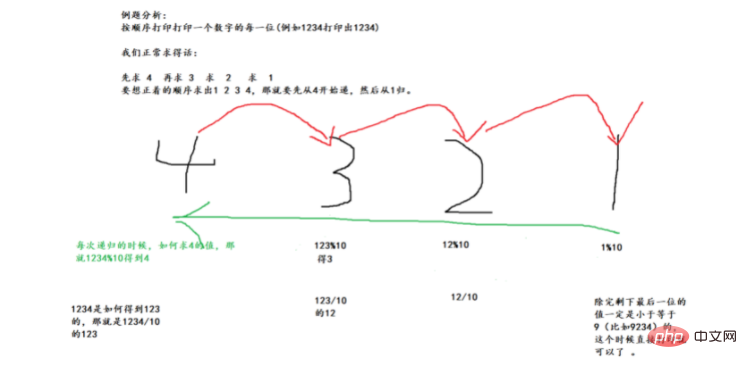
Implementation code:
public class TestDemo {
public static void print(int n){
if(n < 10){
System.out.print(n+" ");
}else{
print(n/10);
System.out.print(n%10+" ");
}
}
public static void main(String[] args) {
print(1234);
}
}Example: Write a recursive method and input a non-negative integer , returns the sum of the numbers that make up it. For example: if you enter 1729, it should return 1 7 2 9
Implementation code:
public class TestDemo {
public static int sumEveryone(int n){
if(n < 10){
return n;
}else{
return n%10 + sumEveryone(n/10);
}
}
public static void main(String[] args) {
System.out.println(sumEveryone(7910));
}
}Example question: Find the nth Fibonacci number
Drawing analysis:

Implementation code:
第一种方法:递归
public class TestDemo {
public static int fib(int n){
if(n == 1 || n == 2){
return 1;
}else{
return fib(n-2)+fib(n-1);
}
}
public static void main(String[] args) {
System.out.println(fib(5));
}
第二种方法:叫做循环(迭代)实现
public static int fib2(int n){
if(n == 1 || n==2){
return 1;
}
int f1 = 1;
int f2 = 1;
int f3 = 0;
for (int i = 3; i < n; i++) {
f3 = f1+f2;
f1 = f2;
f2 = f3;
}
return f3;
}
public static void main(String[] args) {
System.out.println(fib2(45));
}The above is the detailed content of Java Recursion: Concepts and Usage. For more information, please follow other related articles on the PHP Chinese website!




