How to implement an undirected graph in Java?

Basic concepts

Definition of graph

A graph is composed of a point set V={v_i} A tuple consisting of a set E={e_k} of unordered pairs of elements in VV is recorded as G=(V,E), and the element v_{i## in V # is called a vertex, and the element e}k _{in E is called an edge.}

For two points u, v in V, if the edge (u, v) belongs to E, then the two points u and v are said to be adjacent, and u and v are called the endpoints of the edge (u, v) .

We can use m(G)=|E| to represent the number of edges in graph G, and n(G)=|V| to represent the number of vertices in graph G.

Definition of undirected graph

For any edge (vi, vj) in E, if the endpoints of the edge (vi, vj) are unordered, it is an undirected edge. At this time Graph G is called an undirected graph. Undirected graph is the simplest graph model. The following figure shows the same undirected graph. The vertices are represented by circles, and the edges are the connections between vertices without arrows (picture from "Algorithm 4th Edition"):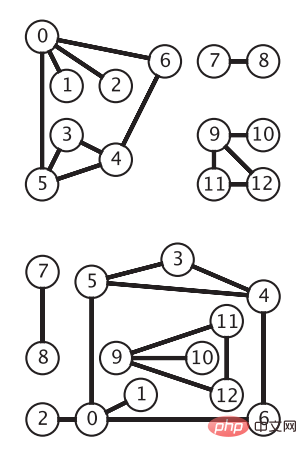

API of undirected graph

For an undirected graph, we care about the number of vertices, the number of edges, the sum of the adjacent vertices of each vertex and The edge addition operation, so the interface is as follows:

package com.zhiyiyo.graph;

/**
 * 无向图
 */
public interface Graph {
    /**
     * 返回图中的顶点数
     */
    int V();

    /**
     * 返回图中的边数
     */
    int E();

    /**
     * 向图中添加一条边
     * @param v 顶点 v
     * @param w 顶点 w
     */
    void addEdge(int v, int w);

    /**
     * 返回所有相邻顶点
     * @param v 顶点 v
     * @return 所有相邻顶点
     */
    Iterable<Integer> adj(int v);
}

Implementation method of undirected graph

Adjacency matrix

Using a matrix to represent a graph is often used to study the properties and applications of graphs It is more convenient. There are various matrix representation methods for various graphs, such as weight matrix and adjacency matrix. Here we only focus on the adjacency matrix. It is defined as:

For the graph G=(V,E), |V|=n, construct a matrix A=(a

ij₎n×n _{, where:}

# Then matrix A is called the adjacency matrix of graph G.

It can be seen from the definition that we can use a two-dimensional Boolean array

A to implement the adjacency matrix. When A[i][j] = true, the vertex i and j are adjacent.

For a graph G with n vertices, the space consumed by the adjacency matrix is ​​the size of n

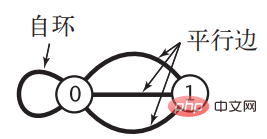
2 ^{Boolean values, which will cause a lot of waste for sparse graphs. When the number of vertices When it is very large, the space consumed will be an astronomical figure. At the same time, when the graph is special and has self-loops and parallel edges, the adjacency matrix representation is powerless. "Algorithm" gives graphs with these two situations:}

#Array of edges

For undirected graphs, we can implement a class

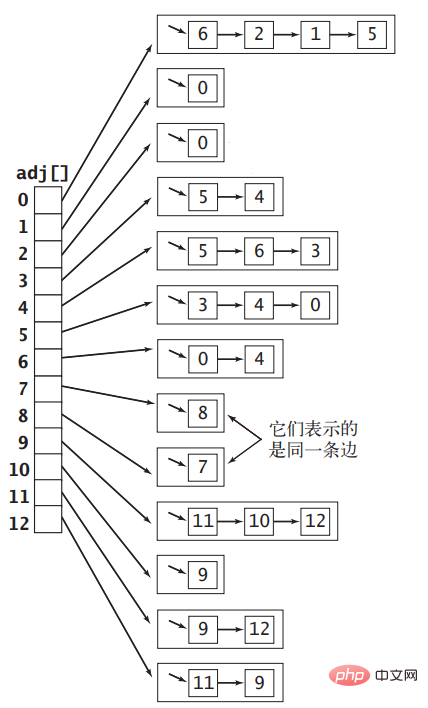
Edge, only two instance variables are used to store the two vertices u and v, and then all Edge can be saved in an array. There is a big problem with this, that is, when obtaining all adjacent vertices of vertex v, you must traverse the entire array to obtain them. The time complexity is O(|E|). Since obtaining adjacent vertices is a very common operation, This way of expressing it doesn't work either.

Adjacency list array

If we represent the vertex as an integer with a value range of 0∼|V|−1, then we can use an array of length |V| The index represents each vertex, and each array element is then set to a linked list on which other vertices adjacent to the vertex represented by the index are mounted. The undirected graph shown in Figure 1 can be represented by the adjacency list array shown in the following figure:

The code for using the adjacency list to implement the undirected graph is as follows, since Each linked list in the adjacency list array will save the vertices adjacent to the vertex, so when adding edges to the graph, you need to add nodes to the two linked lists in the array:

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.stack.LinkStack;

/**
 * 使用邻接表实现的无向图
 */
public class LinkGraph implements Graph {
    private final int V;
    private int E;
    private LinkStack<Integer>[] adj;

    public LinkGraph(int V) {
        this.V = V;
        adj = (LinkStack<Integer>[]) new LinkStack[V];
        for (int i = 0; i < V; i++) {
            adj[i] = new LinkStack<>();
        }
    }

    @Override
    public int V() {
        return V;
    }

    @Override
    public int E() {
        return E;
    }

    @Override
    public void addEdge(int v, int w) {
        adj[v].push(w);
        adj[w].push(v);
        E++;
    }

    @Override
    public Iterable<Integer> adj(int v) {
        return adj[v];
    }
}

used here The stack code is as follows. The implementation of the stack is not the focus of this blog, so I won’t explain too much here:

package com.zhiyiyo.collection.stack;

import java.util.EmptyStackException;
import java.util.Iterator;

/**
 * 使用链表实现的堆栈
 */
public class LinkStack<T> {
    private int N;
    private Node first;

    public void push(T item) {
        first = new Node(item, first);
        N++;
    }

    public T pop() throws EmptyStackException {
        if (N == 0) {
            throw new EmptyStackException();
        }

        T item = first.item;
        first = first.next;
        N--;
        return item;
    }

    public int size() {
        return N;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    public Iterator<T> iterator() {
        return new ReverseIterator();
    }

    private class Node {
        T item;
        Node next;

        public Node() {
        }

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }


    private class ReverseIterator implements Iterator<T> {
        private Node node = first;

        @Override
        public boolean hasNext() {
            return node != null;
        }

        @Override
        public T next() {
            T item = node.item;
            node = node.next;
            return item;
        }

        @Override
        public void remove() {
        }
    }
}

Traversal of undirected graphs

Given the following picture, now It is required to find the path from each vertex to vertex 0. How to achieve this? Or to put it simply, given vertices 0 and 4, it is required to determine whether starting from vertex 0 can reach vertex 4. How to achieve this? This requires the use of two graph traversal methods: depth-first search and breadth-first search.

Before introducing these two traversal methods, let’s first give the API that needs to be implemented to solve the above problems:

package com.zhiyiyo.graph;

public interface Search {
    /**
     * 起点 s 和 顶点 v 之间是否连通
     * @param v 顶点 v
     * @return 是否连通
     */
    boolean connected(int v);

    /**
     * 返回与顶点 s 相连通的顶点个数（包括 s）
     */
    int count();

    /**
     * 是否存在从起点 s 到顶点 v 的路径
     * @param v 顶点 v
     * @return 是否存在路径
     */
    boolean hasPathTo(int v);

    /**
     * 从起点 s 到顶点 v 的路径，不存在则返回 null
     * @param v 顶点 v
     * @return 路径
     */
    Iterable<Integer> pathTo(int v);
}

深度优先搜索

深度优先搜索的思想类似树的先序遍历。我们从顶点 0 开始，将它的相邻顶点 2、1、5 加到栈中。接着弹出栈顶的顶点 2，将它相邻的顶点 0、1、3、4 添加到栈中，但是写到这你就会发现一个问题：顶点 0 和 1明明已经在栈中了，如果还把他们加到栈中，那这个栈岂不是永远不会变回空。所以还需要维护一个数组 boolean[] marked，当我们将一个顶点 i 添加到栈中时，就将 marked[i] 置为 true，这样下次要想将顶点 i 加入栈中时，就得先检查一个 marked[i] 是否为 true，如果为 true 就不用再添加了。重复栈顶节点的弹出和节点相邻节点的入栈操作，直到栈为空，我们就完成了顶点 0 可达的所有顶点的遍历。

为了记录每个顶点到顶点 0 的路径，我们还需要一个数组 int[] edgeTo。每当我们访问到顶点 u 并将其一个相邻顶点 i 压入栈中时，就将 edgeTo[i] 设置为 u，说明要想从顶点i 到达顶点 0，需要先回退顶点 u，接着再从顶点 edgeTo[u] 处获取下一步要回退的顶点直至找到顶点 0。

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.stack.LinkStack;
import com.zhiyiyo.collection.stack.Stack;


public class DepthFirstSearch implements Search {
    private boolean[] marked;
    private int[] edgeTo;
    private Graph graph;
    private int s;
    private int N;

    public DepthFirstSearch(Graph graph, int s) {
        this.graph = graph;
        this.s = s;
        marked = new boolean[graph.V()];
        edgeTo = new int[graph.V()];
        dfs();
    }

    /**
     * 递归实现的深度优先搜索
     *
     * @param v 顶点 v
     */
    private void dfs(int v) {
        marked[v] = true;
        N++;
        for (int i : graph.adj(v)) {
            if (!marked[i]) {
                edgeTo[i] = v;
                dfs(i);
            }
        }
    }

    /**
     * 堆栈实现的深度优先搜索
     */
    private void dfs() {
        Stack<Integer> vertexes = new LinkStack<>();
        vertexes.push(s);
        marked[s] = true;

        while (!vertexes.isEmpty()) {
            Integer v = vertexes.pop();
            N++;

            // 将所有相邻顶点加到堆栈中
            for (Integer i : graph.adj(v)) {
                if (!marked[i]) {
                    edgeTo[i] = v;
                    marked[i] = true;
                    vertexes.push(i);
                }
            }
        }
    }

    @Override
    public boolean connected(int v) {
        return marked[v];
    }

    @Override
    public int count() {
        return N;
    }

    @Override
    public boolean hasPathTo(int v) {
        return connected(v);
    }

    @Override
    public Iterable<Integer> pathTo(int v) {
        if (!hasPathTo(v)) return null;
        Stack<Integer> path = new LinkStack<>();

        int vertex = v;
        while (vertex != s) {
            path.push(vertex);
            vertex = edgeTo[vertex];
        }

        path.push(s);
        return path;
    }
}

广度优先搜索

广度优先搜索的思想类似树的层序遍历。与深度优先搜索不同，从顶点 0 出发，广度优先搜索会先处理完所有与顶点 0 相邻的顶点 2、1、5 后，才会接着处理顶点 2、1、5 的相邻顶点。这个搜索过程就是一圈一圈往外扩展、越走越远的过程，所以可以用来获取顶点 0 到其他节点的最短路径。只要将深度优先搜索中的堆换成队列，就能实现广度优先搜索：

package com.zhiyiyo.graph;

import com.zhiyiyo.collection.queue.LinkQueue;

public class BreadthFirstSearch implements Search {
    private boolean[] marked;
    private int[] edgeTo;
    private Graph graph;
    private int s;
    private int N;

    public BreadthFirstSearch(Graph graph, int s) {
        this.graph = graph;
        this.s = s;
        marked = new boolean[graph.V()];
        edgeTo = new int[graph.V()];
        bfs();
    }

    private void bfs() {
        LinkQueue<Integer> queue = new LinkQueue<>();
        marked[s] = true;
        queue.enqueue(s);

        while (!queue.isEmpty()) {
            int v = queue.dequeue();
            N++;

            for (Integer i : graph.adj(v)) {
                if (!marked[i]) {
                    edgeTo[i] = v;
                    marked[i] = true;
                    queue.enqueue(i);
                }
            }
        }
    }
}

队列的实现代码如下：

package com.zhiyiyo.collection.queue;


import java.util.EmptyStackException;


public class LinkQueue<T> {
    private int N;
    private Node first;
    private Node last;

    public void enqueue(T item) {
        Node node = new Node(item, null);
        if (++N == 1) {
            first = node;
        } else {
            last.next = node;
        }
        last = node;
    }

    public T dequeue() throws EmptyStackException {
        if (N == 0) {
            throw new EmptyStackException();
        }

        T item = first.item;
        first = first.next;
        if (--N == 0) {
            last = null;
        }
        return item;
    }

    public int size() {
        return N;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    private class Node {
        T item;
        Node next;

        public Node() {
        }

        public Node(T item, Node next) {
            this.item = item;
            this.next = next;
        }
    }
}

The above is the detailed content of How to implement an undirected graph in Java?. For more information, please follow other related articles on the PHP Chinese website!