New research reveals the potential of quantum Monte Carlo to surpass neural networks in breaking through limitations, and a Nature sub-issue details the latest progress

After four months, another collaborative work between ByteDance Research and Chen Ji’s research group at the School of Physics at Peking University has been published in top international publications Nature Communications: the paper "Towards the ground state of molecules via diffusion Monte Carlo on neural networks 》Combines the neural network with the diffusion Monte Carlo method, greatly improving the computational accuracy, efficiency and system scale of the neural network method in quantum chemistry-related tasks, becoming the latest SOTA.

• Paper link:
  ​​https://www.nature.com/articles/s41467-023-37609-3​
• ##Code address:
  ​##​https://github.com/bytedance/jaqmc​
Introduction

The author applies the trial wave function based on the neural network to the diffusion Monte Carlo method (Diffusion Monte Carlo, or DMC) of the fixed node surface to accurately calculate atomic and molecular systems with different electronic properties.

The diffusion Monte Carlo method is one of the commonly used methods in the field of quantum chemistry to accurately calculate the ground state energy of molecules and materials. By combining it with the diffusion Monte Carlo method, the authors significantly improved the computational accuracy and efficiency of the neural network SOTA method in quantum chemistry. In addition, the author also proposed an extrapolation method based on empirical linear relationships, which greatly improved the calculation of molecular binding energy. Overall, this computational framework serves as a high-precision method for solving quantum many-body problems and provides a more powerful tool for in-depth understanding of the properties of chemical molecules.

Quantum Monte Carlo method based on neural network

Since 2018, multiple research groups have applied neural networks to variable In the Variational Monte Carlo method (Variational Monte Carlo, or VMC) [1,2,3], more accurate molecular ground state energy is obtained with the help of the powerful expression ability of neural networks. When this work was published in 2022, the SOTA work in the neural network-based variational Monte Carlo method was FermiNet [2] proposed by DeepMind in 2019, which was able to obtain very accurate results on a smaller scale system. However, the accuracy of the variational Monte Carlo method is limited by the expression ability of the neural network, and there will be increasingly obvious accuracy problems when dealing with larger systems. In addition, this type of method converges very slowly when dealing with larger systems, posing a huge challenge to computing resources.

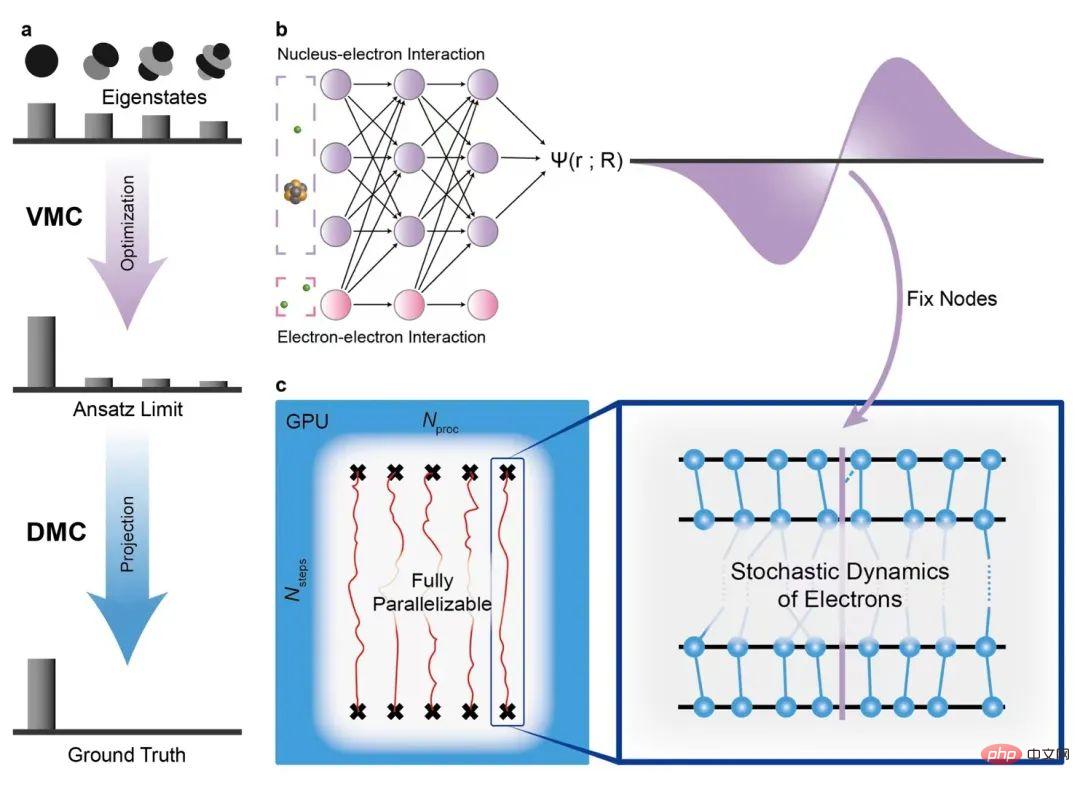
The diffusion Monte Carlo method is one of the classic high-precision algorithms in the field of quantum chemistry. It has excellent characteristics such as high accuracy, good parallelizability, and is suitable for large-scale calculations. In addition, diffusion Monte Carlo can break through the limitations of the expression ability of neural networks and use projection algorithms to surpass the accuracy of the variational Monte Carlo method.

In this work, the author combines SOTA's neural network (FermiNet) as a trial wave function with the diffusion Monte Carlo method. The new calculation method significantly improves the accuracy and reduces the number of required calculation steps compared to FermiNet. The diffusion Monte Carlo software designed and implemented in this work is neural network friendly, GPU friendly, and parallel friendly. It can be combined with a wide range of neural network wave functions to automatically improve its accuracy and efficiency.

Calculation results

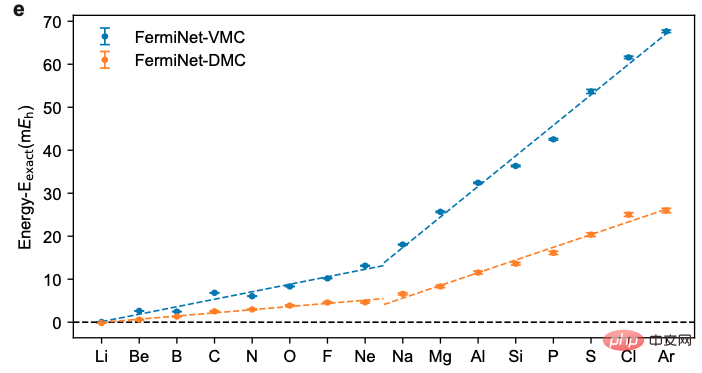
1. Atom​

Use neural network to perform calculation on large molecular systems During quantum Monte Carlo calculations, due to limitations in computing power, the expression capabilities of the neural networks that can be used are also subject to certain limitations. To simulate this scenario, the authors used only two layers of neural networks to study the second and third rows of atoms. The calculation results show that as the system becomes larger, the accuracy of the variational Monte Carlo method becomes worse and worse, while the accuracy improvement brought by the diffusion Monte Carlo method becomes more and more obvious.

2. Molecule​

The author also verified the effectiveness of the neural network-based diffusion Monte Carlo method on a series of molecular systems, including nitrogen molecules, cyclobutadiene and double water molecules. Significant improvements in computational accuracy were observed on all tested systems.

3. Benzene ring and biphenyl ring​

This work Before its publication, the neural network wave function method based on variational Monte Carlo in the field of quantum chemistry had only dealt with small molecules within 30 electrons. This work applies the neural network wave function method to systems with 42 to 84 electrons, namely benzene rings and biphenyl rings, for the first time. The calculation results show that the diffusion Monte Carlo method is significantly better than the variational Monte Carlo method in accuracy, and can achieve the same or better accuracy with one order of magnitude fewer calculation steps.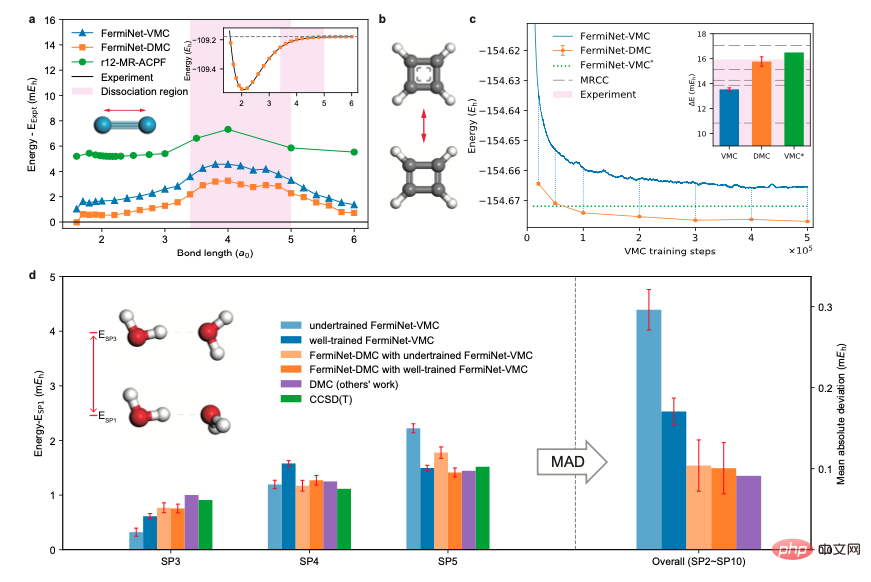

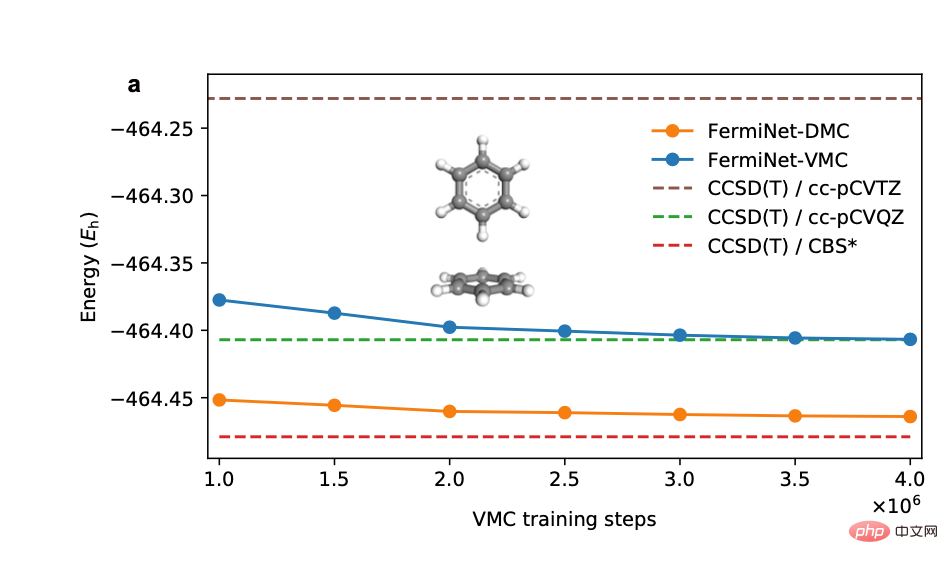
##4. Linear relationship and extrapolation method ​

When the author examined the energy corresponding to different training stages of the neural network, he found that the calculation results of variational Monte Carlo and diffusion Monte Carlo were empirical in many systems. linear relationship (left picture below). Using this linear relationship to extrapolate the dissociation energy calculation of the diphenyl ring significantly improves the calculation accuracy and obtains results that are consistent with chemical experiments (right picture below).

Conclusion and Outlook

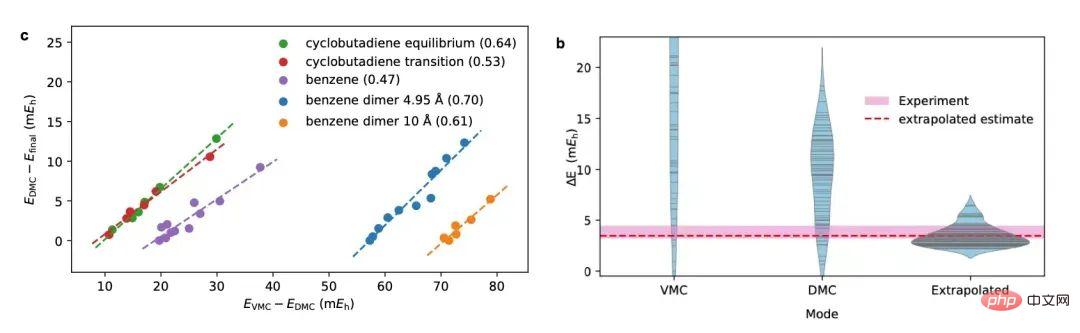
This work shows that the diffusion Monte Carlo method based on neural networks is superior in both accuracy and efficiency. for the variational Monte Carlo method. The author's open-source diffusion Monte Carlo code can be quickly combined with the continuously innovative neural networks [4,5] in the field of quantum chemistry to empower the research community. In addition, the diffusion Monte Carlo method can also be combined with a series of methods such as periodic neural networks [6] and neural networks with pseudopotentials [7] that deal with real solids to improve computing effects on corresponding tasks.

The above is the detailed content of New research reveals the potential of quantum Monte Carlo to surpass neural networks in breaking through limitations, and a Nature sub-issue details the latest progress. For more information, please follow other related articles on the PHP Chinese website!