By converting mathematical problems into code, Google's research has greatly improved the accuracy of machine proofs.

Computers have been used to verify mathematical proofs for some time, but they were only able to do so if the problems were prepared using a specially designed proof language and could not handle the mixture of mathematical notation and written text used by mathematicians .

If you convert mathematical problems written in natural language into formal code and make them easier for computers to solve, it may help build machines that can explore new discoveries in mathematics.

This process is called formalisation, but just one proof can take years of work, so only a small part of mathematical knowledge is formalized and then proven by machines.

Autoformalization refers to the task of automatically translating mathematics from natural language to formal language. The practical and philosophical implications of a successful automated formalization tool would be enormous, it could reduce the current excessive formalization costs, and in the long run, it could connect automated aspects of mathematical reasoning in various research areas.

In a recent study, Google's Yuhuai Wu and his collaboratorsused neural networks from OpenAI Codex to automate formalization work. Codex has been trained on large amounts of text and programming data from the web, and programmers can use it to generate reliable code.

Paper link: https://arxiv.org/pdf/2205.12615.pdf

Formalizing 12,500 middle school mathematics competition problems

A series of recent advances in large-scale language models demonstrate the potential of models to understand formal languages. However, existing successes have been limited to formal languages ​​(such as Python) for which large corpora exist on the web. In contrast, formal mathematical data is very scarce. One of the largest formal mathematical language libraries, Archive of Formal Proofs, is only 180mb in size, which is less than 0.18% of the training data of the large language model Codex.

Furthermore, unlike the case for general-purpose programming languages, where natural language docstrings are widely available, there is little alignment of data between natural languages ​​and formal mathematical languages. Therefore, it is still unknown whether the success of large-scale language models can directly promote the development of automatic formalization.

Given the similarities between proof languages ​​and programming languages, the team decided to see if Codex could formalize a library of 12,500 middle school math competition problems. It is able to convert a quarter of the problems into a format compatible with the formal proof solver Isabelle.

Wu said many unsuccessful conversions are the result of the system not understanding certain mathematical concepts. "If you show the model with an example that explains the concept, then the model can quickly grasp it."

This work explores the prospects of automatic formalization of large language models. The researchers found that large language models Already have a pretty good ability to formalize natural language mathematics in an interactive theorem prover.

Figure 1 below is a perfect example of automatic formalization. Not only does the model convert syntactically correct Isabelle code, it is also able to capture important reasoning points in natural language.

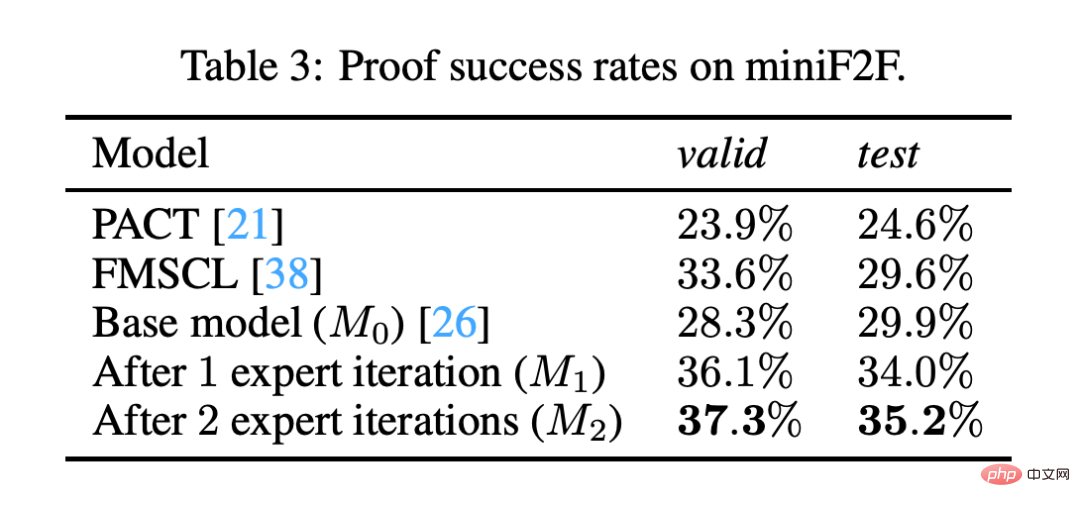
To test the effectiveness of this automated formalization process, the team then applied Codex to a set of problems that already had human formalized versions, for which the Codex was also generated Developed its own formalized version. The team used another AI called MiniF2F to solve both versions of the problem.

Automatically formalizing the problem increases MiniF2F’s success rate from 29% to 35%, indicating that Codex has made important progress in problem formalization.

It is worth noting that presentations in many mathematics competitions tend to be of the form: one is asked to find the answer to a certain problem, rather than to prove a given proposition. However, formal mathematical statements are in the form of propositions, not questions.

In order to convert a question into a proposition, the researcher attached "The Final Answer" after the question:

is used for automatic formalization The prompt format is:

Will AI compete with human mathematicians?

It's an interesting development, but Wu says the team's work is just a proof of concept. "If the goal is to train a machine that is comparable to the top human mathematicians, then automatic formalization seems to be the key path to achieve this goal."

Albert Jiang, a member of the Cambridge University team, said that if the success rate is further improved, AI will be able to compete with human mathematicians. "If we reach 100%, we will definitely create an AI agent that wins the International Mathematical Olympiad gold medal."

The team's immediate goal is to improve automatic formal models and automation Proof of the machine, but the future impact of the research findings will be far more profound. Wu says these models can reveal areas of mathematics currently unknown to humans.

The reasoning capabilities of this machine are also very suitable for verification tasks in a wider range of fields. "You can verify that a piece of software does exactly what you want it to do, or you can verify a hardware chip, so it has applications in financial trading algorithms and hardware design."

Using machines to explore mathematics is an exciting Excited about the development, says Yang-Hui He of the Institute of Mathematical Sciences in London, but the real challenge is using the model in mathematical research that is mostly written in LaTex. "We only use LaTex because it is smooth to type, but it is a natural language in a sense and has its own rules."

He said, because users can define their own functions and Notations, these functions and symbols may only be used in one mathematics paper, which can be tricky for neural networks trained only on plain text.

The above is the detailed content of By converting mathematical problems into code, Google's research has greatly improved the accuracy of machine proofs.. For more information, please follow other related articles on the PHP Chinese website!