
Today I would like to introduce to you a multivariate time series prediction article posted on arixv in 2023.1. The starting point is quite interesting: how to improve the fairness of multivariate time series. The modeling methods used in this article are all conventional operations that have been used in space-time prediction, Domain Adaptation, etc., but the point of multi-variable fairness is relatively new.

Fairness issues, It is a macro concept in the field of machine learning. One understanding of fairness in machine learning is the consistency of the fitting effect of a model on different samples. If a model performs well on some samples and poorly on other samples, then the model is less fair. For example, a common scenario is that in a recommendation system, the model's prediction effect on head samples is better than that on tail samples, which reflects the unfairness of the model's prediction effect on different samples.
Back to the problem of multivariate time series prediction, fairness refers to whether the model has a better prediction effect on each variable. If the model's prediction effect on different variables is very different, then this multivariate time series forecasting model is unfair. For example, in the example in the figure below, the first row of the table is the variance of the MAE of the prediction effects of various models on each variable. It can be seen that there is a certain degree of unfairness in different models. The sequence in the picture below is an example. Some sequences are better at predicting, while others are worse at predicting.
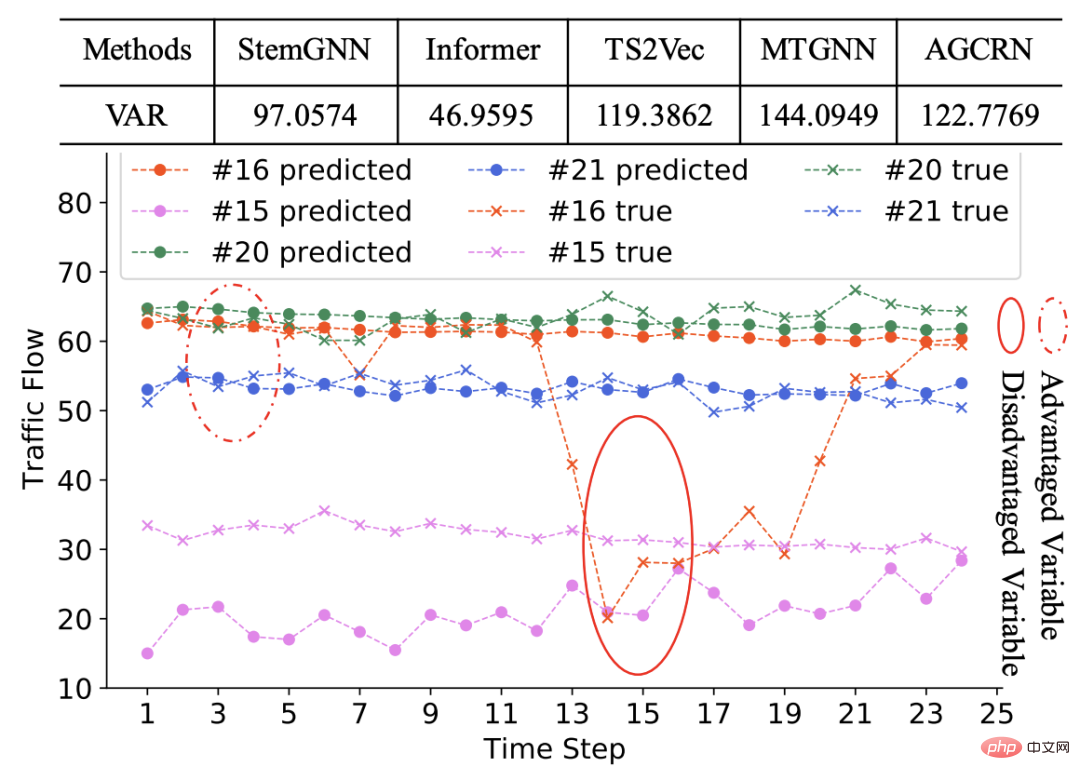
Why does unfairness occur? Whether in multivariate time series or in other machine learning fields, one of the major reasons for the large differences in prediction effects of different samples is that different samples have different characteristics, and the model may be dominated by the characteristics of certain samples during the training process, resulting in The model predicts well on samples that dominate training, but poorly on non-dominated samples.
In multivariate time series, different variables may have very different sequence patterns. For example, in the example shown above, most of the sequences are stationary, which dominates the model training process. A small number of sequences exhibit different volatility from other sequences, resulting in poor prediction performance of the model on these sequences.
How to solve the unfairness in multivariate time series? One way of thinking is that since the unfairness is caused by the different characteristics of different sequences, if the commonalities between the sequences and the differences between the sequences can be decomposed and modeled independently, the above-mentioned problems can be alleviated. question.
This article is based on this idea. The overall architecture is to use the clustering method to group multi-variable sequences and obtain the common features of each group; further use the adversarial learning method to learn from the original representation. Peel off the information unique to each group and obtain common information. Through the above process, the public information and sequence-specific information are separated, and the final prediction is made based on these two parts of information.
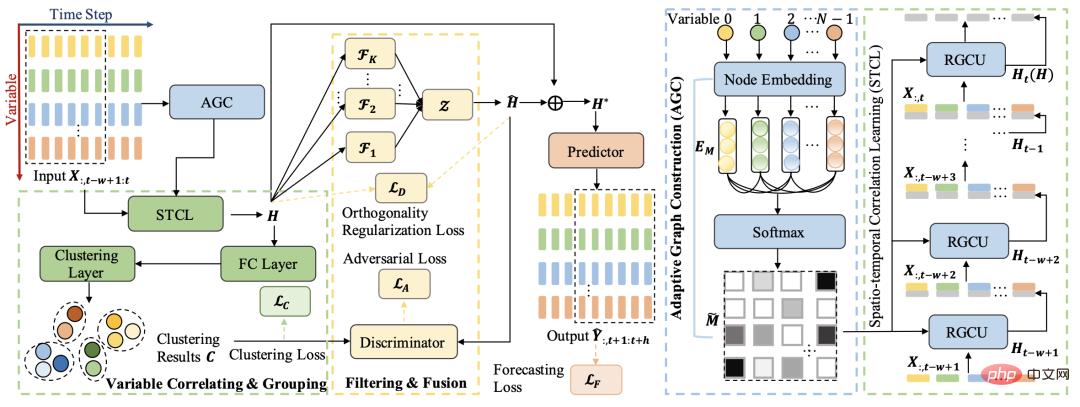
The overall model structure mainly includes 4 modules: multi-variable sequence relationship learning, spatiotemporal relationship network, sequence clustering, and decomposition study.
One of the key points of multivariate time series is to learn the relationship between each sequence. This article uses the Spatial-Temporal method to learn this relationship. Since multivariate time series is not like many spatiotemporal prediction tasks, the relationship between various variables can be defined in advance, so the automatic learning method of adjacency matrix is used here. The specific calculation logic is to generate a randomly initialized embedding for each variable, and then use the inner product of the embedding and some post-processing to calculate the relationship between the two variables as the elements at the corresponding positions of the adjacency matrix. The formula is as follows:
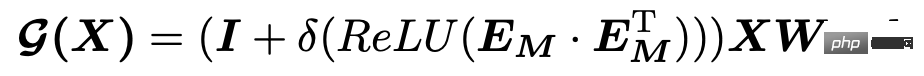
This method of automatically learning adjacency matrices is very commonly used in spatio-temporal forecasting, in Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks (KDD 2020), REST : This approach is adopted in articles such as Reciprocal Framework for Spatiotemporal-coupled Prediction (WWW 2021). I have introduced the principle implementation of the relevant model in detail in the Planet article KDD2020 classic space-time prediction model MTGNN code analysis. Interested students can read further.
After having the adjacency matrix, the article uses a graph time series prediction model to spatio-temporally encode the multi-variable time series to obtain the representation of each variable sequence. The specific model structure is very similar to DCRNN. Based on GRU, the GCN module is introduced into the calculation of each unit. It can be understood that in the calculation process of each unit of the normal GRU, the vector of the neighbor node is introduced to do a GCN to obtain an updated representation. Regarding the implementation code principle of DCRNN, you can refer to this article on DCRNN model source code analysis.
After obtaining the representation of each variable time series, the next step is to cluster these representations to obtain the grouping of each variable sequence, and then extract the unique characteristics of each group of variables. Information. The following loss function is introduced in this article to guide the clustering process, where H represents the representation of each variable sequence, and F represents the affiliation of each variable sequence with K categories.
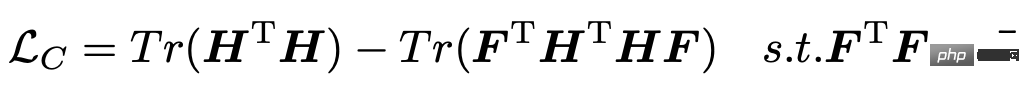
The update process of this loss function requires the use of the EM algorithm, that is, fixing the sequence to represent H, optimizing F, and fixing F, optimizing H. The method adopted in this article is to use SVD to update the matrix F once after training several rounds of models to obtain the representation H.
The core of the decomposition learning module is to distinguish the public representation and private representation of each category variable. The public representation refers to the characteristics shared by the sequence of each cluster variable, and the private representation Refers to the unique characteristics of the variable sequence within each cluster. In order to achieve this goal, the paper adopts the ideas of decomposition learning and adversarial learning to separate the representation of each cluster from the original sequence representation. The cluster representation represents the characteristics of each class, and the stripped representation represents the commonality of all sequences. Using this common representation for prediction can achieve fairness in predicting each variable.
This article uses the idea of adversarial learning to directly calculate the L2 distance between the public representation and the private representation (that is, the representation of each cluster obtained by clustering), and uses this as a reverse optimization of loss to let the public part represent The gap with private representation is as wide as possible. In addition, an orthogonal constraint will be added to make the inner product of the public representation and the private representation close to 0.
The experiments in this article are mainly compared from two aspects: fairness and prediction effect. The compared models include basic time series prediction models (LSTNet, Informer), graph time series prediction Models etc. In terms of fairness, the variance of the prediction results of different variables is used. Through comparison, the fairness of this method is significantly improved compared to other models (as shown in the table below).
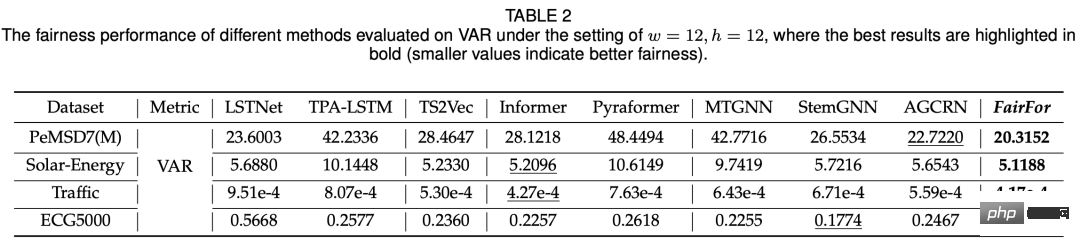
In terms of prediction effect, the model proposed in this article can basically achieve equivalent results to SOTA:
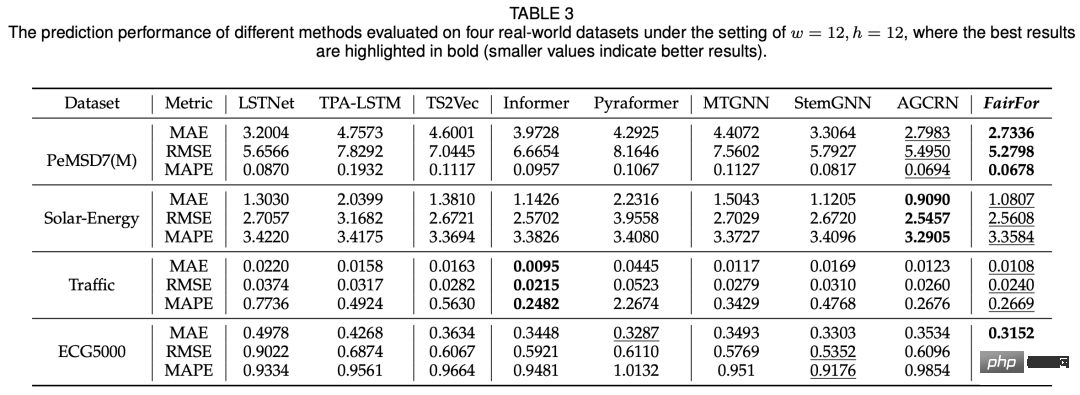
The above is the detailed content of On the issue of fairness in multivariate time series. For more information, please follow other related articles on the PHP Chinese website!
 mybatis first level cache and second level cache
mybatis first level cache and second level cache
 What to do if your IP address is attacked
What to do if your IP address is attacked
 Solution to the problem that the input is not supported when the computer starts up
Solution to the problem that the input is not supported when the computer starts up
 What is the article tag used to define?
What is the article tag used to define?
 Introduction to input functions in c language
Introduction to input functions in c language
 How to use rank function
How to use rank function
 Win10 pauses updates
Win10 pauses updates
 How to set the width of fieldset
How to set the width of fieldset
 Detailed explanation of setinterval
Detailed explanation of setinterval




