 Backend Development
Backend Development
 Python Tutorial
Python Tutorial
 How to use dendrogram to implement visual clustering in Python
How to use dendrogram to implement visual clustering in Python
How to use dendrogram to implement visual clustering in Python
Dendogram
A dendrogram is a diagram that shows hierarchical relationships between objects, groups, or variables. A dendrogram consists of branches connected at nodes or clusters that represent groups of observations with similar characteristics. The height of a branch or the distance between nodes indicates how different or similar the groups are. That is, the longer the branches or the greater the distance between nodes, the less similar the groups are. The shorter the branches or the smaller the distance between nodes, the more similar the groups are.
Dendograms are useful for visualizing complex data structures and identifying subgroups or clusters of data with similar characteristics. They are commonly used in biology, genetics, ecology, social sciences, and other fields where data can be grouped based on similarity or correlation.
Background knowledge:
The word "dendrogram" comes from the Greek words "dendron" (tree) and "gramma" (drawing). In 1901, British mathematician and statistician Karl Pearson used a tree diagram to show the relationship between different plant species [1]. He called this graph a "cluster graph." This can be considered the first use of dendrograms.
Data preparation
We will use the real stock prices of several companies for clustering. For easy access, data is collected using the free API provided by Alpha Vantage. Alpha Vantage provides both free API and premium API. Access through the API requires a key, please refer to his website.
import pandasaspd
import requests
companies={'Apple':'AAPL','Amazon':'AMZN','Facebook':'META','Tesla':'TSLA','Alphabet (Google)':'GOOGL','Shell':'SHEL','Suncor Energy':'SU',
'Exxon Mobil Corp':'XOM','Lululemon':'LULU','Walmart':'WMT','Carters':'CRI','Childrens Place':'PLCE','TJX Companies':'TJX',
'Victorias Secret':'VSCO','MACYs':'M','Wayfair':'W','Dollar Tree':'DLTR','CVS Caremark':'CVS','Walgreen':'WBA','Curaleaf':'CURLF'}Twenty companies were selected from technology, retail, oil and gas and other industries.
import time
all_data={}
forkey,valueincompanies.items():
# Replace YOUR_API_KEY with your Alpha Vantage API key
url=f'https://www.alphavantage.co/query?function=TIME_SERIES_DAILY_ADJUSTED&symbol={value}&apikey=<YOUR_API_KEY>&outputsize=full'
response=requests.get(url)
data=response.json()
time.sleep(15)
if'Time Series (Daily)'indataanddata['Time Series (Daily)']:
df=pd.DataFrame.from_dict(data['Time Series (Daily)'], orient='index')
print(f'Received data for {key}')
else:
print("Time series data is empty or not available.")
df.rename(columns= {'1. open':key}, inplace=True)
all_data[key]=df[key]The above code sets a 15-second pause between API calls to ensure that it will not be blocked too frequently.
# find common dates among all data frames
common_dates=None
fordf_key, dfinall_data.items():
ifcommon_datesisNone:
common_dates=set(df.index)
else:
common_dates=common_dates.intersection(df.index)
common_dates=sorted(list(common_dates))
# create new data frame with common dates as index
df_combined=pd.DataFrame(index=common_dates)
# reindex each data frame with common dates and concatenate horizontally
fordf_key, dfinall_data.items():
df_combined=pd.concat([df_combined, df.reindex(common_dates)], axis=1)Integrate the above data into the DF we need, which can be used directly below
Hierarchical clustering
Hierarchical clustering is a kind of application Clustering algorithms for machine learning and data analysis. It uses a hierarchy of nested clusters to group similar objects into clusters based on similarity. The algorithm can be either agglomerative, which starts with single objects and merges them into clusters, or divisive, which starts with a large cluster and recursively divides it into smaller clusters.
It should be noted that not all clustering methods are hierarchical clustering methods, and dendrograms can only be used on a few clustering algorithms.
Clustering Algorithm We will use hierarchical clustering provided in scipy module.
1. Top-down clustering
import numpyasnp import scipy.cluster.hierarchyassch import matplotlib.pyplotasplt # Convert correlation matrix to distance matrix dist_mat=1-df_combined.corr() # Perform top-down clustering clustering=sch.linkage(dist_mat, method='complete') cuts=sch.cut_tree(clustering, n_clusters=[3, 4]) # Plot dendrogram plt.figure(figsize=(10, 5)) sch.dendrogram(clustering, labels=list(df_combined.columns), leaf_rotation=90) plt.title('Dendrogram of Company Correlations (Top-Down Clustering)') plt.xlabel('Companies') plt.ylabel('Distance') plt.show()
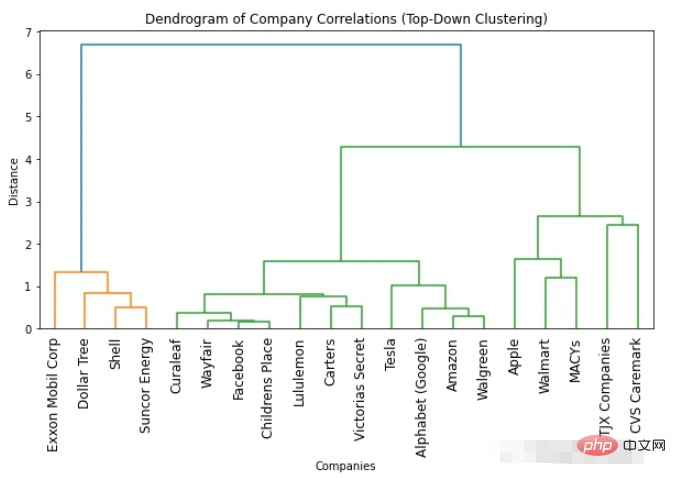
##How to determine the optimal number of clusters based on the dendrogram
The easiest way to find the optimal number of clusters is to look at the number of colors used in the resulting dendrogram. The optimal number of clusters is one less than the number of colors. So according to the dendrogram above, the optimal number of clusters is two. Another way to find the optimal number of clusters is to identify points where the distance between clusters suddenly changes. This is called the "inflection point" or "elbow point" and can be used to determine the number of clusters that best captures the variation in the data. We can see in the above figure that the maximum distance change between different numbers of clusters occurs between 1 and 2 clusters. So again, the optimal number of clusters is two.Get any number of clusters from the dendrogram
One advantage of using a dendrogram is that you can cluster objects into any number of clusters by looking at the dendrogram in clusters. For example, if you need to find two clusters, you can look at the top vertical line on the dendrogram and decide on the clusters. For example, in this example, if two clusters are required, then there are four companies in the first cluster and 16 companies in the second cluster. If we need three clusters we can further split the second cluster into 11 and 5 companies. If you need more, you can follow this example.2. Bottom-up clustering
import numpyasnp import scipy.cluster.hierarchyassch import matplotlib.pyplotasplt # Convert correlation matrix to distance matrix dist_mat=1-df_combined.corr() # Perform bottom-up clustering clustering=sch.linkage(dist_mat, method='ward') # Plot dendrogram plt.figure(figsize=(10, 5)) sch.dendrogram(clustering, labels=list(df_combined.columns), leaf_rotation=90) plt.title('Dendrogram of Company Correlations (Bottom-Up Clustering)') plt.xlabel('Companies') plt.ylabel('Distance') plt.show()
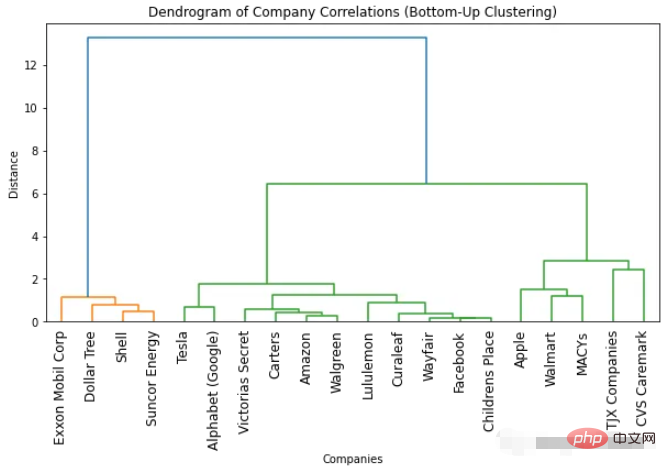 ##The dendrogram we obtained for bottom-up clustering Similar to top-down clustering. The optimal number of clusters is still two (based on the number of colors and the "inflection point" method). But if we require more clusters, some subtle differences will be observed. This is normal because the methods used are different, resulting in slight differences in the results.
##The dendrogram we obtained for bottom-up clustering Similar to top-down clustering. The optimal number of clusters is still two (based on the number of colors and the "inflection point" method). But if we require more clusters, some subtle differences will be observed. This is normal because the methods used are different, resulting in slight differences in the results.
The above is the detailed content of How to use dendrogram to implement visual clustering in Python. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Is there any mobile app that can convert XML into PDF?
Apr 02, 2025 pm 08:54 PM
Is there any mobile app that can convert XML into PDF?
Apr 02, 2025 pm 08:54 PM
An application that converts XML directly to PDF cannot be found because they are two fundamentally different formats. XML is used to store data, while PDF is used to display documents. To complete the transformation, you can use programming languages and libraries such as Python and ReportLab to parse XML data and generate PDF documents.
 How to convert XML files to PDF on your phone?
Apr 02, 2025 pm 10:12 PM
How to convert XML files to PDF on your phone?
Apr 02, 2025 pm 10:12 PM
It is impossible to complete XML to PDF conversion directly on your phone with a single application. It is necessary to use cloud services, which can be achieved through two steps: 1. Convert XML to PDF in the cloud, 2. Access or download the converted PDF file on the mobile phone.
 Is there a mobile app that can convert XML into PDF?
Apr 02, 2025 pm 09:45 PM
Is there a mobile app that can convert XML into PDF?
Apr 02, 2025 pm 09:45 PM
There is no APP that can convert all XML files into PDFs because the XML structure is flexible and diverse. The core of XML to PDF is to convert the data structure into a page layout, which requires parsing XML and generating PDF. Common methods include parsing XML using Python libraries such as ElementTree and generating PDFs using ReportLab library. For complex XML, it may be necessary to use XSLT transformation structures. When optimizing performance, consider using multithreaded or multiprocesses and select the appropriate library.
 What is the process of converting XML into images?
Apr 02, 2025 pm 08:24 PM
What is the process of converting XML into images?
Apr 02, 2025 pm 08:24 PM
To convert XML images, you need to determine the XML data structure first, then select a suitable graphical library (such as Python's matplotlib) and method, select a visualization strategy based on the data structure, consider the data volume and image format, perform batch processing or use efficient libraries, and finally save it as PNG, JPEG, or SVG according to the needs.
 How to open xml format
Apr 02, 2025 pm 09:00 PM
How to open xml format
Apr 02, 2025 pm 09:00 PM
Use most text editors to open XML files; if you need a more intuitive tree display, you can use an XML editor, such as Oxygen XML Editor or XMLSpy; if you process XML data in a program, you need to use a programming language (such as Python) and XML libraries (such as xml.etree.ElementTree) to parse.
 How to beautify the XML format
Apr 02, 2025 pm 09:57 PM
How to beautify the XML format
Apr 02, 2025 pm 09:57 PM
XML beautification is essentially improving its readability, including reasonable indentation, line breaks and tag organization. The principle is to traverse the XML tree, add indentation according to the level, and handle empty tags and tags containing text. Python's xml.etree.ElementTree library provides a convenient pretty_xml() function that can implement the above beautification process.
 Is the conversion speed fast when converting XML to PDF on mobile phone?
Apr 02, 2025 pm 10:09 PM
Is the conversion speed fast when converting XML to PDF on mobile phone?
Apr 02, 2025 pm 10:09 PM
The speed of mobile XML to PDF depends on the following factors: the complexity of XML structure. Mobile hardware configuration conversion method (library, algorithm) code quality optimization methods (select efficient libraries, optimize algorithms, cache data, and utilize multi-threading). Overall, there is no absolute answer and it needs to be optimized according to the specific situation.
 How to control the size of XML converted to images?
Apr 02, 2025 pm 07:24 PM
How to control the size of XML converted to images?
Apr 02, 2025 pm 07:24 PM
To generate images through XML, you need to use graph libraries (such as Pillow and JFreeChart) as bridges to generate images based on metadata (size, color) in XML. The key to controlling the size of the image is to adjust the values of the <width> and <height> tags in XML. However, in practical applications, the complexity of XML structure, the fineness of graph drawing, the speed of image generation and memory consumption, and the selection of image formats all have an impact on the generated image size. Therefore, it is necessary to have a deep understanding of XML structure, proficient in the graphics library, and consider factors such as optimization algorithms and image format selection.





