
The sorting algorithm uses a specific algorithm factor to process one or more sets of data according to an established pattern. rearrange. The final sequence is presented according to certain rules.
In sorting algorithms, stability and efficiency are issues we often have to consider.
Stability: Stability means that when two identical elements appear in a sequence at the same time, after a certain sorting algorithm, the relative positions of the two before and after sorting do not change.
Complexity analysis:
(1) Time complexity: that is, the process from the initial state of the sequence to the final sorted result state after operations such as transformation and shifting of the sorting algorithm. A measure of time spent.
(2) Space complexity: It is the space overhead spent from the initial state of the sequence through the process of sorting and shift transformation to the final state.
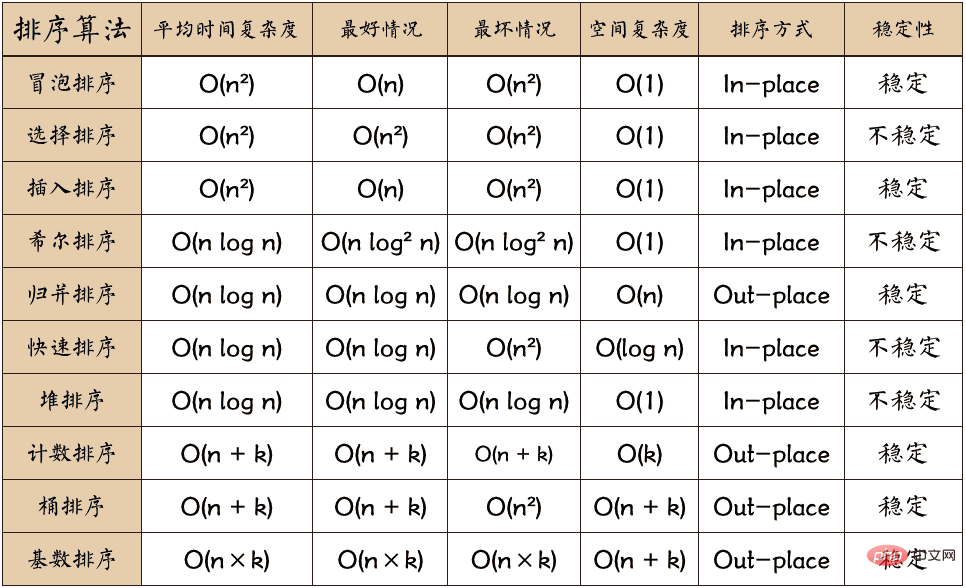
Common sorting algorithms are divided into the following types:
halved insertion sort (Binary Insertion Sort) is an improvement on the insertion sort algorithm. Continuously insert elements into the previously sorted sequence. Since the first half is a sorted sequence, we don't have to search for the insertion point in sequence. We can use the half search method to speed up the search for the insertion point.
In the process of inserting a new element into the sorted array, when looking for the insertion point, set the first element of the area to be inserted to a[low], and the last element If the element is set to a[high], then in each round of comparison, the element to be inserted will be compared with a[m], where m = (low high)/2. If it is smaller than the reference element, select a[low] to a[ m-1] is the new insertion area (i.e. high=m-1), otherwise select a[m 1] to a[high] as the new insertion area (i.e. low=m 1), and so on until low
In short: take advantage of the ordering characteristics of the arranged elements and use the characteristics of half search to quickly find the position to be inserted.
// Binary Insertion Sort method
private static void binaryInsertSort(int[] array){
for(int i = 1; i < array.length; i++){
int temp = array[i];
int low = 0;
int high = i - 1;
while(low <= high){
int mid = (low + high) / 2;
if(temp < array[mid]){
high = mid - 1;
}else{
low = mid + 1;
}
}
for(int j = i; j >= low + 1; j--){
array[j] = array[j - 1];
}
array[low] = temp;
}
}The half insertion sort algorithm is a stable sorting algorithm. It significantly reduces the number of comparisons between keywords compared to the direct insertion algorithm, so it is faster than the direct insertion sort algorithm. Fast, but the number of record moves has not changed, so the time complexity of the halved insertion sort algorithm is still O(n^2), which is the same as the direct insertion sort algorithm.
Time complexity
Best case: O(n). If the elements are sorted in forward order, the position will be found directly at the beginning, without searching and shifting.
Worst case: O(n^2). If the elements are sorted in reverse order, a data lookup is required every time.
Average complexity: O(n^2).
Space complexity: O(1). Only a few storage spaces are needed to record the key units of information, that is, the space complexity is O(1).
Example:
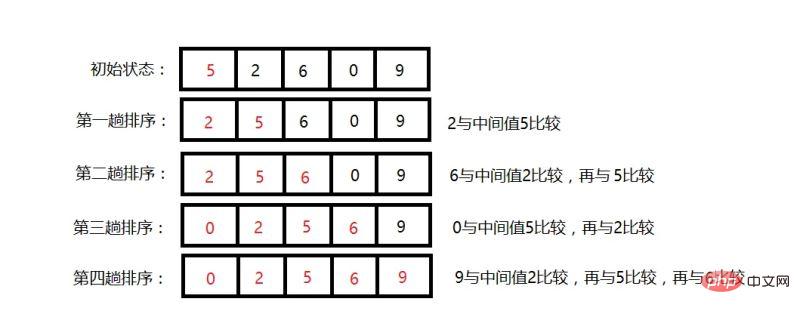
The overall idea of the algorithm has been described above. Let’s use an example to test the water directly. .
Half insertion sort
Problem description:
I give you an integer array nums, please sort the array in ascending order.
Example 1:
Input: nums = [5,2,3,1]
Output: [1,2,3,5]
Example 2:
Input: nums = [5,1,1,2,0,0]
Output: [0,0,1,1,2,5]
Tips:
1 <= nums.length <= 5 * 104
-5 * 104 <= nums[i] <= 5 * 104
class Solution {
public int[] sortArray(int[] nums) {
for(int i = 1; i < nums.length; i++){
int temp = nums[i];
int low = 0;
int high = i - 1;
while(low <= high){
int mid = (low + high) / 2;
if(temp < nums[mid]){
high = mid - 1;
}else{
low = mid + 1;
}
}
for(int j = i; j >= low + 1; j--){
nums[j] = nums[j - 1];
}
nums[low] = temp;
}
return nums;
}
}The above is the detailed content of How to implement half insertion sort algorithm in Java. For more information, please follow other related articles on the PHP Chinese website!




