 Backend Development
Backend Development
 Python Tutorial
Python Tutorial
 Clustering algorithm based on projection on convex sets (POCS)
Clustering algorithm based on projection on convex sets (POCS)
Clustering algorithm based on projection on convex sets (POCS)
POCS: Projections onto Convex Sets. In mathematics, a convex set is a set in which any line segment between any two points is within the set. Projection is the operation of mapping a point to a subspace in another space. Given a convex set and a point, you can operate by finding the projection of the point onto the convex set. The projection is the point in the convex set that is closest to the point and can be calculated by minimizing the distance between this point and any other point in the convex set. Since it is a projection, we can map the features to a convex set in another space, so that operations such as clustering or dimensionality reduction can be performed.
This article reviews a clustering algorithm based on the convex set projection method, that is, a clustering algorithm based on POCS. The original paper was published at IWIS2022.
convex set
A convex set is defined as a set of data points, in which the line segment connecting any two points x1 and x2 in the set is completely included in this set. According to the definition of convex set, the empty set ∅, unitary set, line segment, hyperplane, and Euclidean sphere are all considered to be convex sets. A data point is also considered a convex set because it is a singleton set (a set with only one element). This opens up a new path for applying the concept of POCS to clustered data points.
Projection of Convex Sets (POCS)
POCS methods can be roughly divided into two types: alternating and parallel.
1. Alternating poc
Starting from any point in the data space, the alternating projection from this point to two (or more) intersecting convex sets will converge to the intersection point of the sets. One point, such as the following figure:
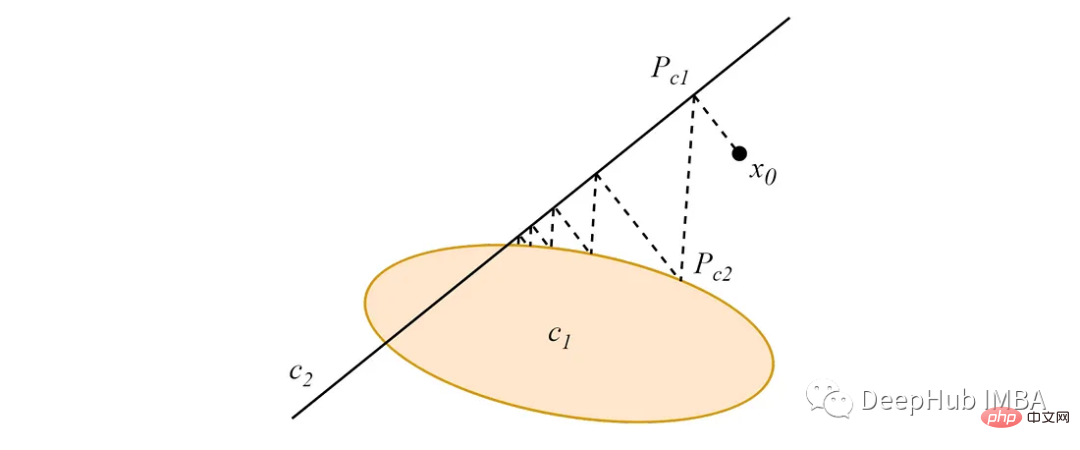
When the convex sets do not intersect, the alternating projection will converge to greedy limit cycles that depend on the projection order.
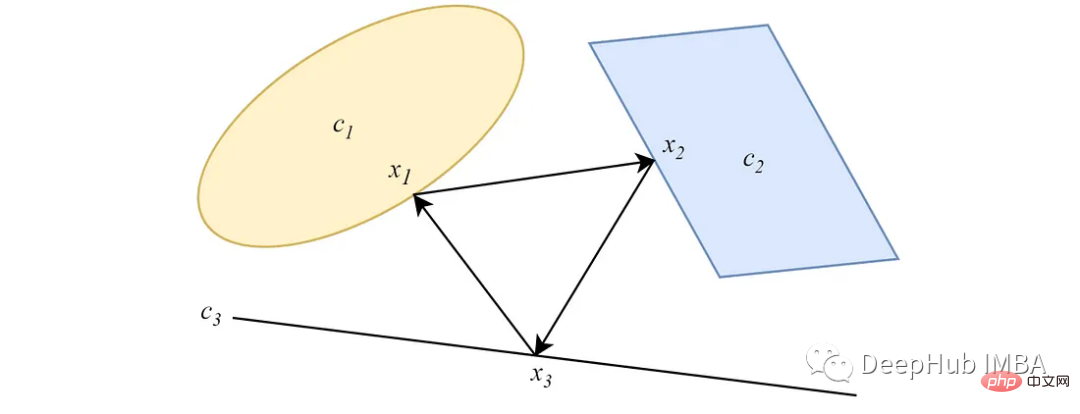
2. Parallel POCS
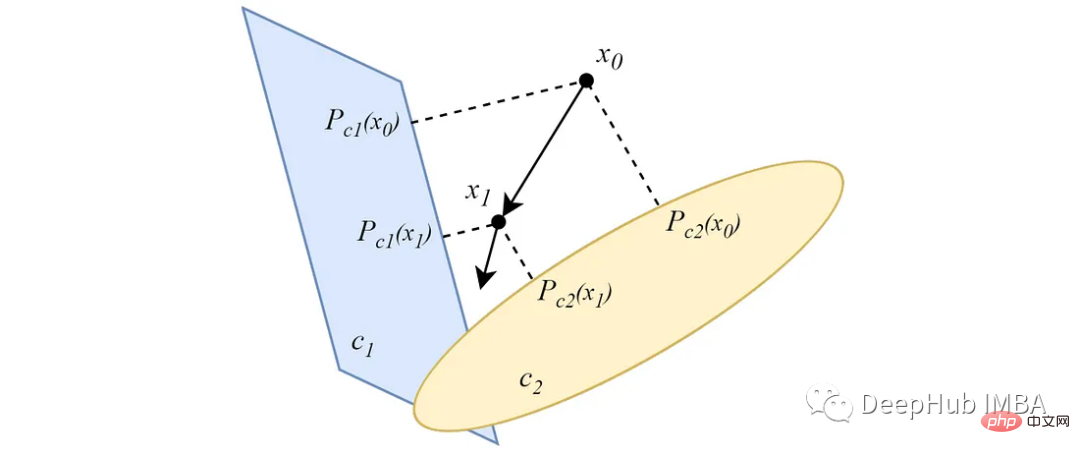
Different from the alternating form, parallel POCS projects from data points to all convex sets simultaneously, and each projection All have an importance weight. For two nonempty intersecting convex sets, similar to the alternating version, the parallel projection converges to a point at the intersection of the sets.
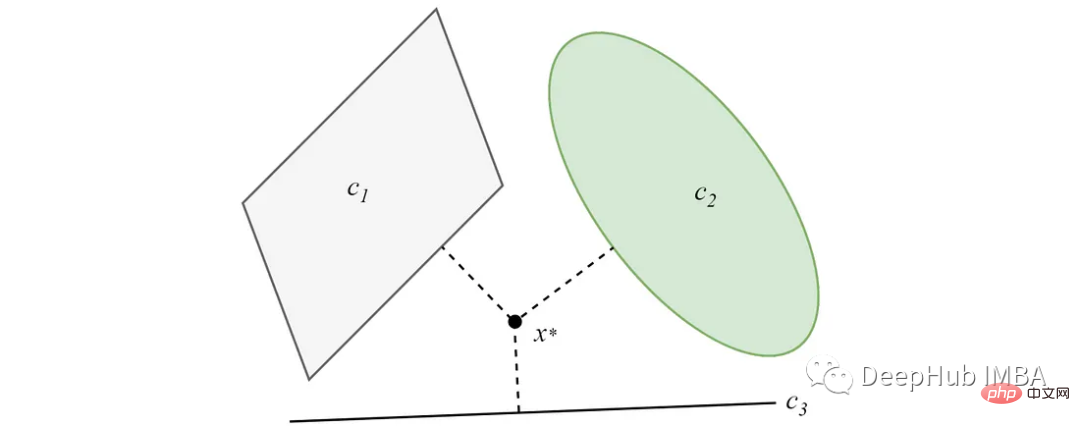
In the case where the convex sets do not intersect, the projection will converge to a minimum solution. The main idea of the POCs-based clustering algorithm comes from this feature.
For more details about POCS, you can view the original paper
Clustering algorithm based on pocs
Using the convergence of the parallel POCS method property, the author of the paper proposed a very simple but effective clustering algorithm to a certain extent. The algorithm works similarly to the classic K-Means algorithm, but there are differences in the way each data point is processed: the K-Means algorithm weights the importance of each data point the same, but the POCs-based clustering algorithm Each data point is weighted differently in importance, which is proportional to the distance of the data point from the cluster prototype.
The pseudo code of the algorithm is as follows:

Experimental results
The author tested the POCs-based algorithm on some public benchmark data sets Performance of clustering algorithms. The table below summarizes the descriptions of these datasets.
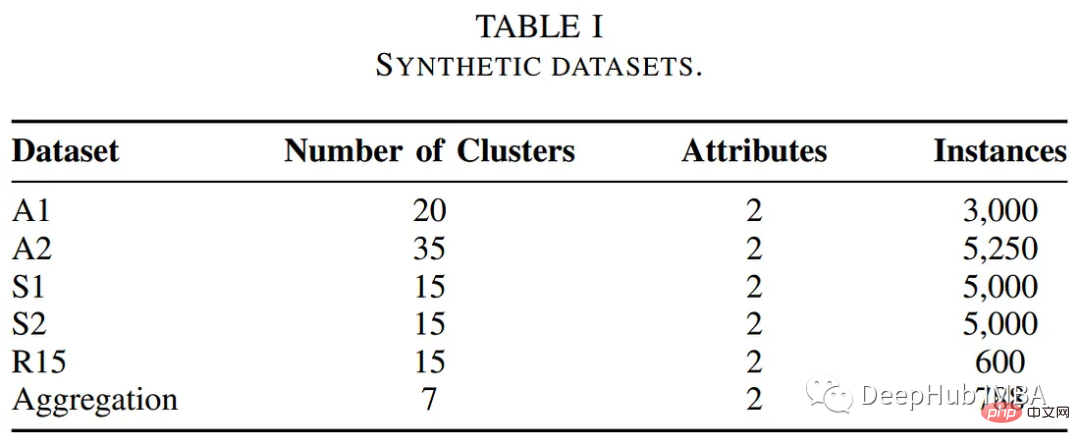
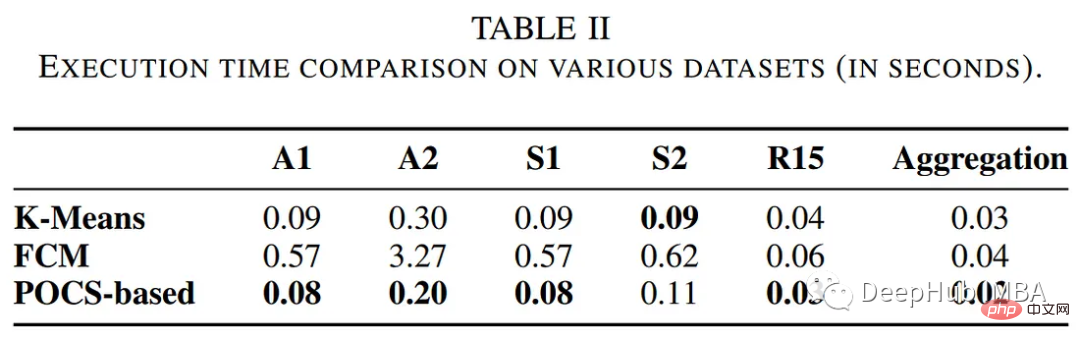
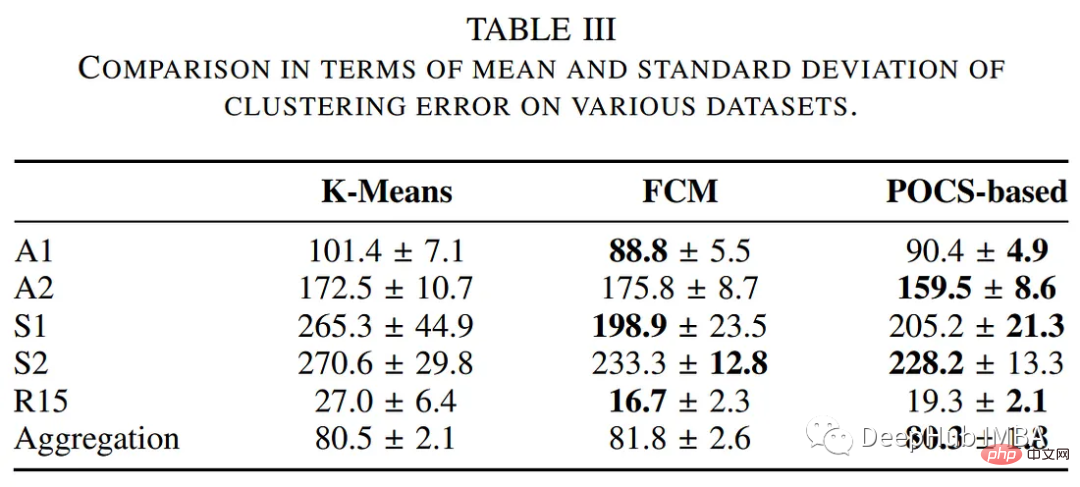
The authors compared the performance of the POCs-based clustering algorithm with other traditional clustering methods, including k-means and fuzzy c-means algorithms. The following table summarizes the evaluation in terms of execution time and clustering error.
The clustering results are shown below:

Example code
We use this algorithm on a very simple data set. The author has released a package for direct use. For applications, we can use it directly:
pip install pocs-based-clustering
Create a simple data set of 5000 data points centered on 10 clusters:
# Import packages import time import matplotlib.pyplot as plt from sklearn.datasets import make_blobs from pocs_based_clustering.tools import clustering # Generate a simple dataset num_clusters = 10 X, y = make_blobs(n_samples=5000, centers=num_clusters, cluster_std=0.5, random_state=0) plt.figure(figsize=(8,8)) plt.scatter(X[:, 0], X[:, 1], s=50) plt.show()

Perform clustering and display the results:
# POSC-based Clustering Algorithm centroids, labels = clustering(X, num_clusters, 100) # Display results plt.figure(figsize=(8,8)) plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis') plt.scatter(centroids[:, 0], centroids[:, 1], s=100, c='red') plt.show()

总结
我们简要回顾了一种简单而有效的基于投影到凸集(POCS)方法的聚类技术,称为基于POCS的聚类算法。该算法利用POCS的收敛特性应用于聚类任务,并在一定程度上实现了可行的改进。在一些基准数据集上验证了该算法的有效性。
论文的地址如下:https://arxiv.org/abs/2208.08888
作者发布的源代码在这里:https://github.com/tranleanh/pocs-based-clustering
The above is the detailed content of Clustering algorithm based on projection on convex sets (POCS). For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
Written above & the author’s personal understanding: At present, in the entire autonomous driving system, the perception module plays a vital role. The autonomous vehicle driving on the road can only obtain accurate perception results through the perception module. The downstream regulation and control module in the autonomous driving system makes timely and correct judgments and behavioral decisions. Currently, cars with autonomous driving functions are usually equipped with a variety of data information sensors including surround-view camera sensors, lidar sensors, and millimeter-wave radar sensors to collect information in different modalities to achieve accurate perception tasks. The BEV perception algorithm based on pure vision is favored by the industry because of its low hardware cost and easy deployment, and its output results can be easily applied to various downstream tasks.
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
The bottom layer of the C++sort function uses merge sort, its complexity is O(nlogn), and provides different sorting algorithm choices, including quick sort, heap sort and stable sort.
 Why is it difficult to implement collection-like functions in Go language?
Mar 24, 2024 am 11:57 AM
Why is it difficult to implement collection-like functions in Go language?
Mar 24, 2024 am 11:57 AM
It is difficult to implement collection-like functions in the Go language, which is a problem that troubles many developers. Compared with other programming languages such as Python or Java, the Go language does not have built-in collection types, such as set, map, etc., which brings some challenges to developers when implementing collection functions. First, let's take a look at why it is difficult to implement collection-like functionality directly in the Go language. In the Go language, the most commonly used data structures are slice and map. They can complete collection-like functions, but
 Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
01 Outlook Summary Currently, it is difficult to achieve an appropriate balance between detection efficiency and detection results. We have developed an enhanced YOLOv5 algorithm for target detection in high-resolution optical remote sensing images, using multi-layer feature pyramids, multi-detection head strategies and hybrid attention modules to improve the effect of the target detection network in optical remote sensing images. According to the SIMD data set, the mAP of the new algorithm is 2.2% better than YOLOv5 and 8.48% better than YOLOX, achieving a better balance between detection results and speed. 02 Background & Motivation With the rapid development of remote sensing technology, high-resolution optical remote sensing images have been used to describe many objects on the earth’s surface, including aircraft, cars, buildings, etc. Object detection in the interpretation of remote sensing images
 Can artificial intelligence predict crime? Explore CrimeGPT's capabilities
Mar 22, 2024 pm 10:10 PM
Can artificial intelligence predict crime? Explore CrimeGPT's capabilities
Mar 22, 2024 pm 10:10 PM
The convergence of artificial intelligence (AI) and law enforcement opens up new possibilities for crime prevention and detection. The predictive capabilities of artificial intelligence are widely used in systems such as CrimeGPT (Crime Prediction Technology) to predict criminal activities. This article explores the potential of artificial intelligence in crime prediction, its current applications, the challenges it faces, and the possible ethical implications of the technology. Artificial Intelligence and Crime Prediction: The Basics CrimeGPT uses machine learning algorithms to analyze large data sets, identifying patterns that can predict where and when crimes are likely to occur. These data sets include historical crime statistics, demographic information, economic indicators, weather patterns, and more. By identifying trends that human analysts might miss, artificial intelligence can empower law enforcement agencies
 Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
1. Background of the Construction of 58 Portraits Platform First of all, I would like to share with you the background of the construction of the 58 Portrait Platform. 1. The traditional thinking of the traditional profiling platform is no longer enough. Building a user profiling platform relies on data warehouse modeling capabilities to integrate data from multiple business lines to build accurate user portraits; it also requires data mining to understand user behavior, interests and needs, and provide algorithms. side capabilities; finally, it also needs to have data platform capabilities to efficiently store, query and share user profile data and provide profile services. The main difference between a self-built business profiling platform and a middle-office profiling platform is that the self-built profiling platform serves a single business line and can be customized on demand; the mid-office platform serves multiple business lines, has complex modeling, and provides more general capabilities. 2.58 User portraits of the background of Zhongtai portrait construction
 PHP algorithm analysis: efficient method to find missing numbers in an array
Mar 02, 2024 am 08:39 AM
PHP algorithm analysis: efficient method to find missing numbers in an array
Mar 02, 2024 am 08:39 AM
PHP algorithm analysis: An efficient method to find missing numbers in an array. In the process of developing PHP applications, we often encounter situations where we need to find missing numbers in an array. This situation is very common in data processing and algorithm design, so we need to master efficient search algorithms to solve this problem. This article will introduce an efficient method to find missing numbers in an array, and attach specific PHP code examples. Problem Description Suppose we have an array containing integers between 1 and 100, but one number is missing. We need to design a





