Java time complexity and space complexity example analysis

1. Algorithm efficiency

Algorithm efficiency analysis is divided into two types: the first is time efficiency, and the second is space efficiency. Time efficiency is called time complexity, and space efficiency is called space complexity. Time complexity mainly measures the running speed of an algorithm, while space complexity mainly measures the extra space required by an algorithm. In the early days of computer development, the storage capacity of computers was very small. So we care a lot about space complexity. However, after the rapid development of the computer industry, the storage capacity of computers has reached a very high level. So we no longer need to pay special attention to the space complexity of an algorithm.

2. Time complexity

1. Concept of time complexity

The time an algorithm takes is proportional to the number of executions of its statements. The basic operations in the algorithm are The number of executions is the time complexity of the algorithm. That is to say, when we get a code and look at the time complexity of the code, we mainly find how many times the code with the most executed statements in the code has been executed.

2. Asymptotic representation of Big O

Look at the picture analysis:

When the value of N becomes larger and larger, the sum of 2N and The value of 10 can be ignored.

In fact, when we calculate the time complexity, we do not actually have to calculate the exact number of executions, but only the approximate number of executions, so here we use the asymptotic representation of Big O.

Big O notation: It is a mathematical symbol used to describe the asymptotic behavior of a function.

1. Replace all additive constants in run time with constant 1.

2. In the modified running times function, only the highest order term is retained.

3. If the highest-order term exists and is not 1, remove the constant multiplied by this term. The result is Big O order.

Through the above we will find that the asymptotic representation of Big O removes those items that have little impact on the results, and expresses the number of executions concisely and clearly.

In addition, the time complexity of some algorithms has best, average and worst cases:

Worst case: the maximum number of runs (upper bound) for any input size

Average case: the expected number of runs for any input size

Best case: the minimum number of runs (lower bound) for any input size

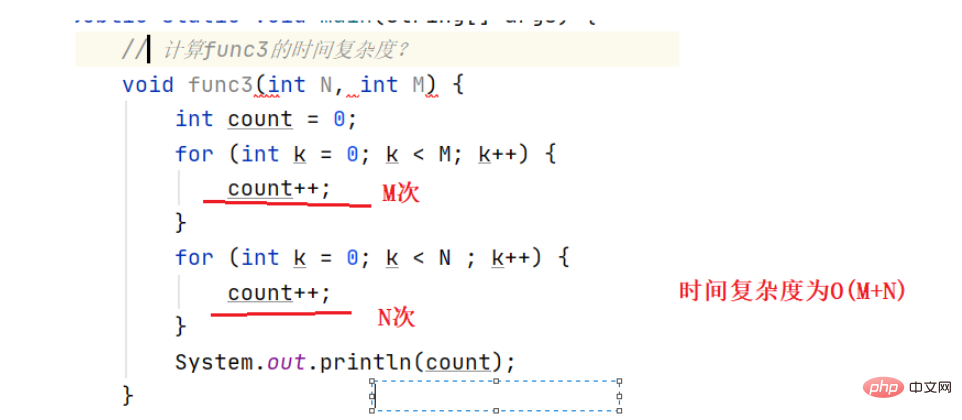
For example: Search for a data x## in an array of length N

#Best case: found 1 time

Worst case: found N times

Average case: found N/2 times

In actual practice, pay attention to the general situation is the worst operating situation of the algorithm, so the time complexity of searching data in the array is O(N)

Calculation time complexity

Example 1:

The basic operation was performed 2N 10 times. By deriving the big O-order method, we know that the time complexity is O(N)

Example 2:

The basic operation is performed M N times, there are two unknowns M and N, the time complexity is O(N M)

Example 3:

The basic operation was performed 100 times. By deriving the big O-order method, the time complexity is O(1)

Example 4: Calculating the time complexity of bubble sort

The basic operation is executed N times at best, and (N*(N-1))/2 times at worst. By deriving the time complexity of the big O-order method, the worst time complexity is generally O( N^2

Example 5: Time complexity of binary search

The basic operation is performed once at best and O(logN) times at worst, time The complexity is O(logN) ps: logN means that the base is 2 and the logarithm is N in algorithm analysis. In some places, it is written as lgN. (It is recommended to explain how logN is calculated through origami search) (because of binary search Each time half of the unsuitable values ​​are eliminated, the remaining values ​​after one halving are: n/2. The remaining values ​​are after two halvings: n/2/2 = n/4)

Example 6: Calculate the time complexity of factorial recursion

The time complexity of recursion = the number of recursions * the number of times each recursion is executed

Through calculation and analysis, it is found that the basic operation is recursed N times, and the time is complex The degree is O(N).

Example 7: Calculate the time complexity of Fibonacci recursion

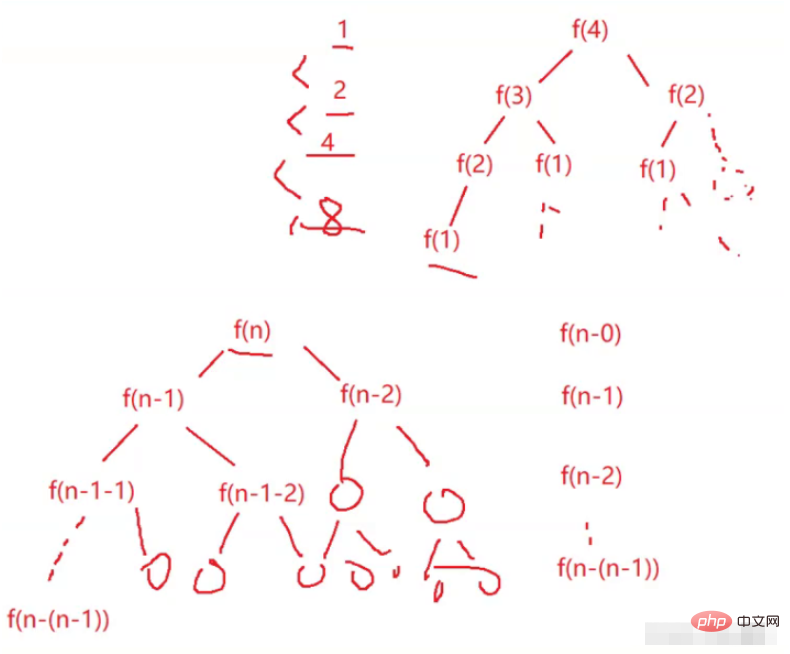
Through calculation and analysis, it is found that the basic operation is recursive 2^N times, and the time complexity is O(2^N).

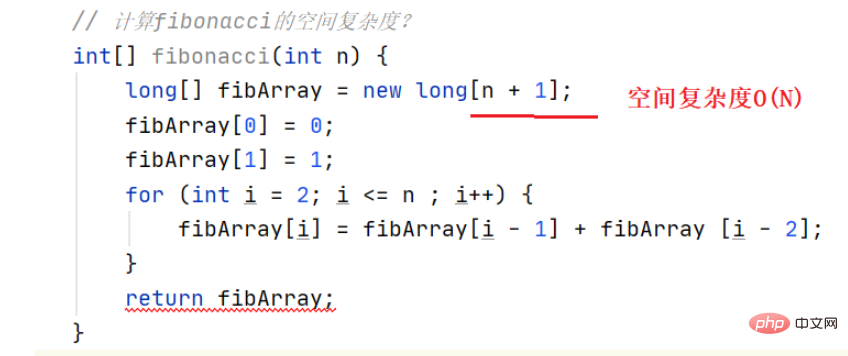
Rule:

## 2^0 2^1 2^2 2^3……2^(n-(n-1))

Sum of geometric sequence

a1 represents the first term, q is geometric, which is 2, 1(1-2^n)/-1 , equivalent to 2^n 1, so the time complexity is O(2^n)

3. Space complexity

Space complexity refers to the temporary occupation of storage by an algorithm during operation A measure of the size of a space. Space complexity is not how many bytes of space the program occupies, because this is not very meaningful, so space complexity is calculated by the number of variables. The space complexity calculation rules are basically similar to the practical complexity, and the big O asymptotic notation is also used.

Example 1: Calculate the space complexity of bubble sort

uses a constant extra space, so the space complexity is O(1)

Example 2: Calculate the space complexity of Fibonacci

N spaces are dynamically opened up, and the space complexity is O(N)

Example 3: Calculate the space complexity of factorial recursion

The recursion is called N times, N stack frames are opened, and each stack frame uses a constant amount of space. The space complexity is O(N)

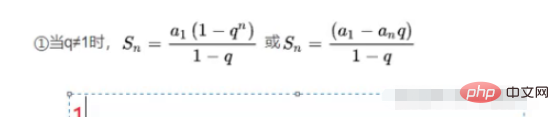
The above is the detailed content of Java time complexity and space complexity example analysis. For more information, please follow other related articles on the PHP Chinese website!