Come and challenge these ten Python questions, will you do it?

Hello, I am Brother Zheng. Python is easy to get started, but difficult to master. Even for experienced engineers, some phenomena are counter-intuitive. The following 10 questions are very interesting and challenging. , the result may make you confused, let’s see how many correct answers you can get?

Here are the questions first, and finally the answers. It is recommended to get a piece of paper first, write down your answers, and finally verify.

Please write the output of the following code:

1. Lazy Python

class A:
def function(self):
return A()
a = A()
A = int
print(a.function())

2. Rounding

>>> round(7 / 2)
>>> round(3 / 2)
>>> round(5 / 2)

3.type and object

>>> isinstance(type, object)
>>> isinstance(object, type)
>>> isinstance(object, object)
>>> isinstance(type, type)

4. Empty Boolean value

>>> any([])
>>> all([])

5. Priority of class internal functions

class A:
answer = 42
def __init__(self):
self.answer = 21
self.__add__ = lambda x, y: x.answer + y
def __add__(self, y):
return self.answer - y
print(A() + 5)

6.Sum

>>> sum("")
>>> sum("", [])
>>> sum("", {})

7. Unexpected attributes

>>> sum([
el.imag 
for el in [
0, 5, 10e9, float('inf'), float('nan')
]
])

8. Output a string that is a multiple of a negative number

>>> "this is a very long string" * (-1)

9. Have seen a negative number 0

max(-0.0, 0.0)

10. Violate the rules of mathematics

>>> x = (1 << 53) + 1
>>> x + 1.0 > x

Answers and explanations

The following results have been verified in Python 3.8.5 version.

1. Lazy Python

class A:
def function(self):
return A()
a = A()
A = int
print(a.function())

The correct result is 0:

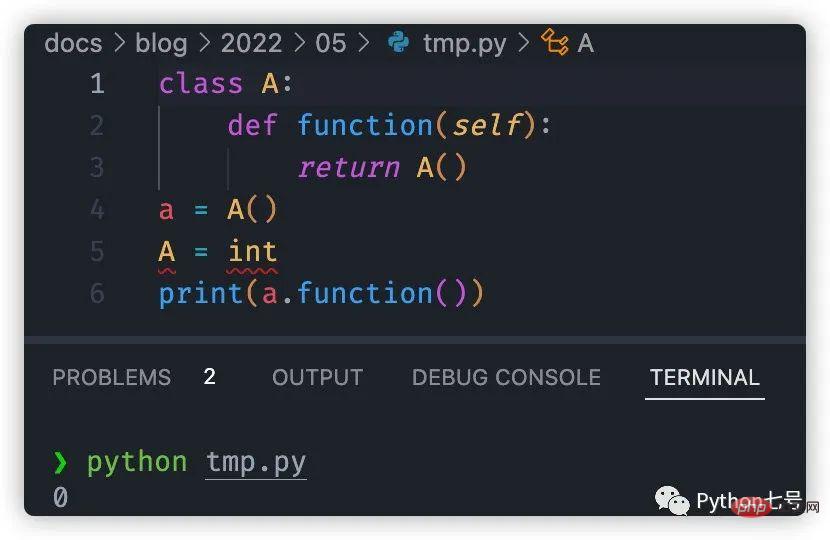
This is not difficult, because the function definition of Python is actually Executable statements and functions do not exist before they are called, and variables are bound only when they are actually called.

In the above example, during function definition, Python allows references to classes or functions that have not yet been defined. However, during execution, A is already of class int, which means that the function method will return a newly created int instance, whose default value is 0.

If there is no A = int, the result is:

2.Rounding

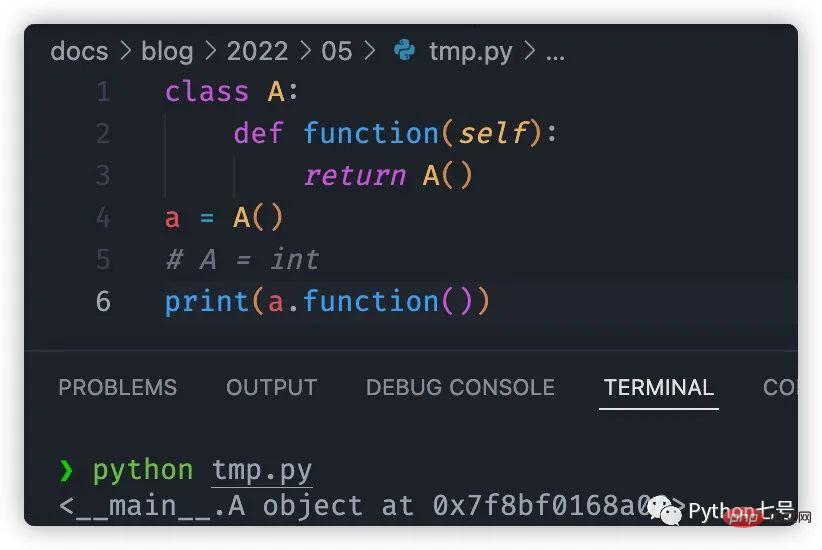
>>> round(7/2)
4
>>> round(3/2)
2
>>> round(5/2)
2

The correct result is 4 2 2, you must feel that the final round(2.5) == 2 is a bit against the rules of mathematics. This is because Python's round method implements banker's rounding [1], in which all half values ​​will be rounded to the nearest even number.

3.type and object

>>> isinstance(type, object)
True
>>> isinstance(object, type)
True
>>> isinstance(object, object)
True
>>> isinstance(type, type)
True
>>>

are both True. I wonder if object and true are the same thing?

In Python, everything is is an object, so any instance check on the object will return True.

isinstance(Anything, object) #=> True。

type represents the metaclass used to construct all Python types. Therefore, all types: int, str, object are instances of type class, which is also an object just like all objects in python. But type is the only object in Python that is an instance of itself.

>>> type(1)
<class 'int'>
>>> type(int)
<class 'type'>
>>> type(type)
<class 'type'>
>>> 

4.Empty Boolean value

>>> any([])
False
>>> all([])
True
>>> any([True,False])
True
>>> all([True,False])
False
>>> 

The results of any and all are a bit unexpected when the parameter is an empty list. But after understanding its checking logic, it makes sense:

Logical operators in Python are lazy. The algorithm of any is to find the element that appears true for the first time. If it is not found, it returns False. The sequence is empty, so no element can be true, so any([]) returns False.

Similarly, the all algorithm searches for the first false element. If it is not found, it returns True. Since there are no false elements in the empty sequence, all([]) returns True. Isn’t this a bit of an empty concept of truth? ?

5.Priority of class internal functions

class A:
answer = 42
def __init__(self):
self.answer = 21
self.__add__ = lambda x, y: x.answer + y
def __add__(self, y):
return self.answer - y
print(A() + 5)

The correct result is: 16:

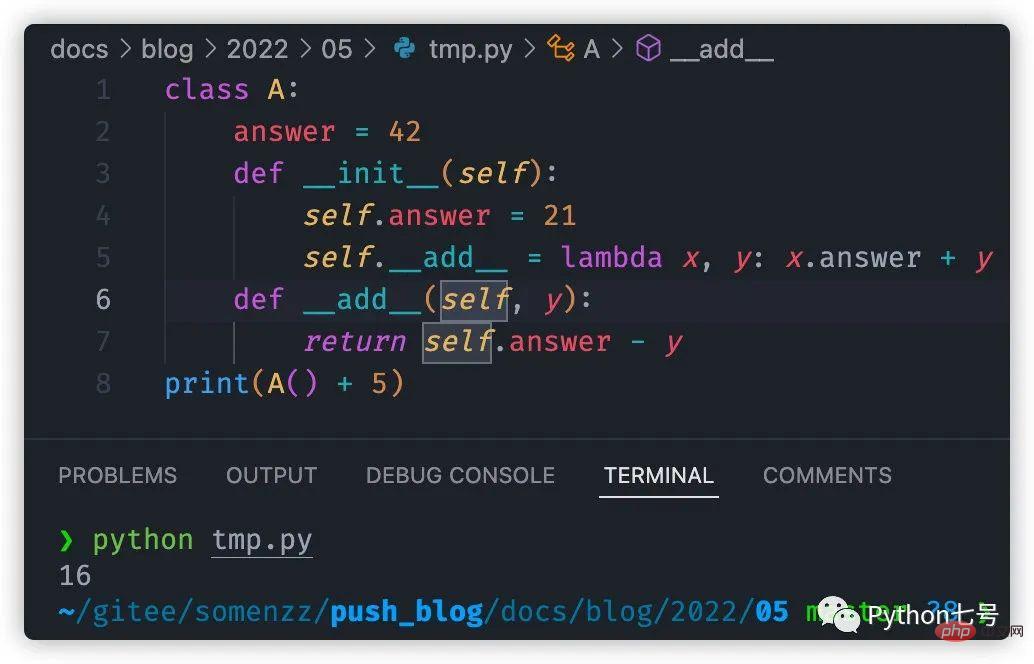
The search order of object functions is: instance level > class level > parent class level. In the above code, the function bound during initialization is the instance level, and the function defined inside the class is the class level.

But magic functions wrapped in double underscores are not within this rule, which means that Python will first look for class-level magic functions.

If you remove the double underline, the result is 26:

##6

.Sum

>>> sum("")
0
>>> sum("", [])
[]
>>> sum("", {})
{}

To figure out what's going on here, we need to check the signature of the sum function:

sum(iterable, /, start=0)

sum sums the items of the iterable starting from left to right and returns the total. iterable is generally a number, and the starting value is not allowed to be a string.

In all cases above, the empty string is treated as an empty sequence, so sum will simply return the starting argument as the total result. In the first case it defaults to zero, for the second and third cases it means the empty list and dictionary passed in as start arguments.

7

.Unexpected attribute

>>> sum([
... el.imag
... for el in [
... 0, 5, 10e9, float('inf'), float('nan')
... ]
... ])
0.0

The above code has an imag attribute, but we did not define it at all, and no error was reported when running. What happened?

This is because all numerical types (int, real, float) in Python inherit from the base object class, and they all support the real and imag attributes, which return the real and imaginary parts respectively. This also includes Infinity and NaN.

8.输出负数倍的字符串

>>> "this is a very long string" * (-1)
''
>>>

正确的结果是 ''，所有的负数倍的字符串，都当作 0 倍，返回 ''。

9.见过负数的 0.0

max(-0.0, 0.0)

为什么会这样?出现这种情况是由于两个原因。负零和零在 Python 中被视为相等。max 的逻辑是，如果多个最大值，返回遇到的第一个。因此 max 函数返回第一次出现的零，它恰好是负数。

10.违反数学规则

>>> x = (1 << 53) + 1
>>> x + 1.0 > x
False

正确的结果是 False，这违反了数学规则啊，为什么呢?

这种违反直觉的行为归咎于三件事：长算术、浮点精度限制和数值比较。

Python 可以支持非常大的整数，如果隐式超过限制则切换计算模式，但 Python 中的浮点精度是有限的。

2⁵³ + 1 = 9007199254740993

是不能完全表示为 Python 浮点数的最小整数。因此，为了执行加 1.0，Python 将 9007199254740993 转换为 float，将其四舍五入为 Python 可以表示的 9007199254740992.0，然后向其添加 1.0，但由于相同的表示限制，它将其设置回 9007199254740992.0：

>>> float(9007199254740993)
9007199254740992.0
>>> 9007199254740992.0 + 1.0
9007199254740992.0
>>>

此外 Python 在 float 与 int 比较时并不会抛出错误，也不会尝试将两个操作数转换为相同的类型。相反，他们比较实际的数值。因为 9007199254740992.0 比 9007199254740993 小，因此 Python 返回 False。

The above is the detailed content of Come and challenge these ten Python questions, will you do it?. For more information, please follow other related articles on the PHP Chinese website!