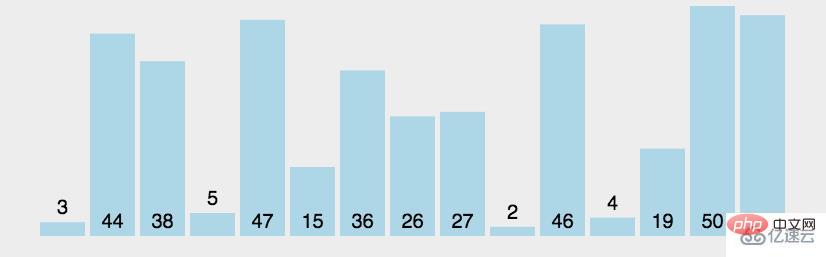
import java.util.Arrays;//冒泡排序public class BubbleSort_01 {
public static void main(String[] args) {
int a[]={3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
//记录比较次数
int count=0;
//i=0,第一轮比较
for (int i = 0; i < a.length-1; i++) {
//第一轮，两两比较
for (int j = 0; j < a.length-1-i; j++) {
if (a[j]>a[j+1]) {
int temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
count++;
}
}
System.out.println(Arrays.toString(a));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
System.out.println("一共比较了："+count+"次");//一共比较了：105次
}}Optimization of Bubble Sort 1:
import java.util.Arrays;public class BubbleSort1_01 {
public static void main(String[] args) {
int a[]={3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
int count=0;
for (int i = 0; i < a.length-1; i++) {
boolean flag=true;
for (int j = 0; j < a.length-1-i; j++) {
if (a[j]>a[j+1]) {
int temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
flag=false;
}
count++;
}
if (flag) {
break;
}
}
System.out.println(Arrays.toString(a));// [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
System.out.println("一共比较了："+count+"次");//一共比较了：95次
}}
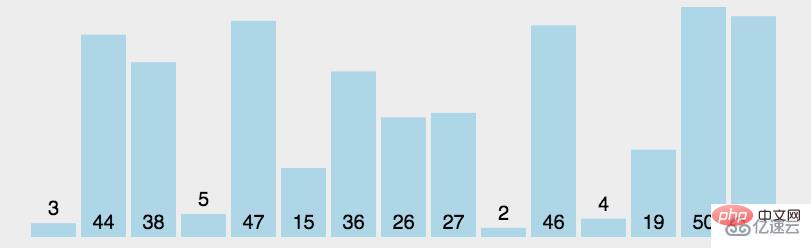
import java.util.Arrays;//选择排序:先定义一个记录最小元素的下标，然后循环一次后面的，找到最小的元素，最后将他放到前面排序好的序列。public class SelectSort_02 {
public static void main(String[] args) {
int a[]={3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
for (int i = 0; i < a.length-1; i++) {
int index=i;//标记第一个为待比较的数
for (int j = i+1; j < a.length; j++) { //然后从后面遍历与第一个数比较
if (a[j]<a[index]) { //如果小,就交换最小值
index=j;//保存最小元素的下标
}
}
//找到最小值后，将最小的值放到第一的位置，进行下一遍循环
int temp=a[index];
a[index]=a[i];
a[i]=temp;
}
System.out.println(Arrays.toString(a));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
}}
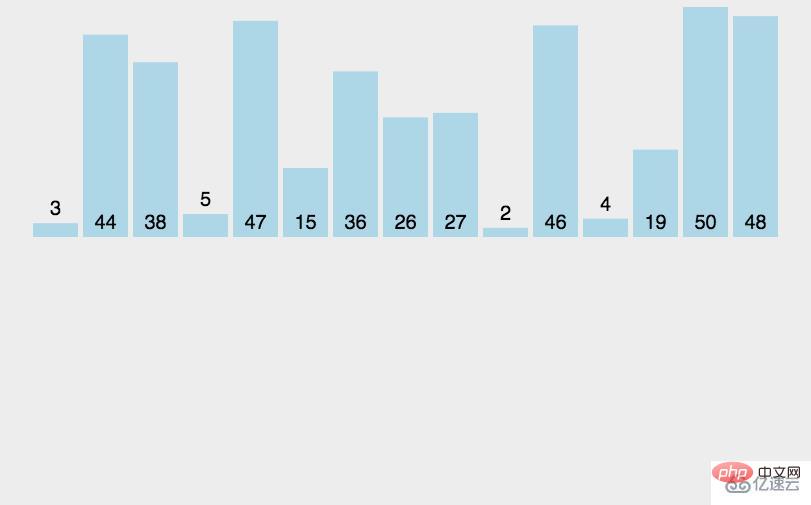
import java.util.Arrays;//插入排序:定义一个待插入的数，再定义一个待插入数的前一个数的下标，然后拿待插入数与前面的数组一一比较，最后交换。public class InsertSort_03 {
public static void main(String[] args) {
int a[]={3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
for (int i = 0; i < a.length; i++) { //长度不减1，是因为要留多一个位置方便插入数
//定义待插入的数
int insertValue=a[i];
//找到待插入数的前一个数的下标
int insertIndex=i-1;
while (insertIndex>=0 && insertValue <a[insertIndex]) {//拿a[i]与a[i-1]的前面数组比较
a[insertIndex+1]=a[insertIndex];
insertIndex--;
}
a[insertIndex+1]=insertValue;
}
System.out.println(Arrays.toString(a));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
}}
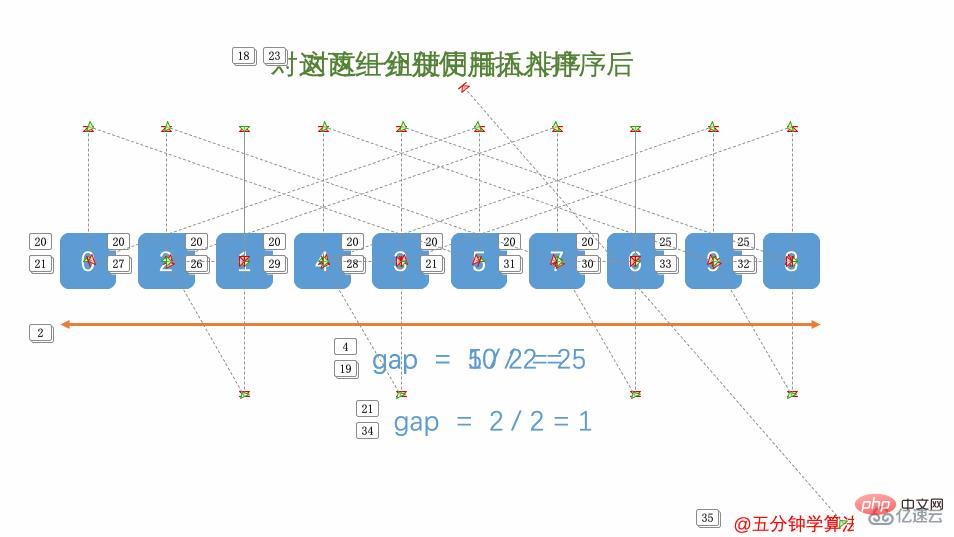
import java.util.Arrays;//希尔排序：插入排序的升级public class ShellSort_04 {
public static void main(String[] args) {
int a[]={3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
int count=0;//比较次数
for (int gap=a.length / 2; gap > 0; gap = gap / 2) {
//将整个数组分为若干个子数组
for (int i = gap; i < a.length; i++) {
//遍历各组的元素
for (int j = i - gap; j>=0; j=j-gap) {
//交换元素
if (a[j]>a[j+gap]) {
int temp=a[j];
a[j]=a[j+gap];
a[j+gap]=temp;
count++;
}
}
}
}
System.out.println(count);//16
System.out.println(Arrays.toString(a));//[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
}}Refer to this blog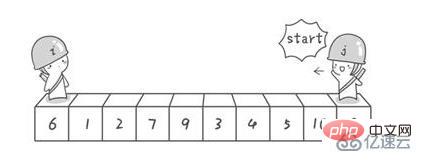
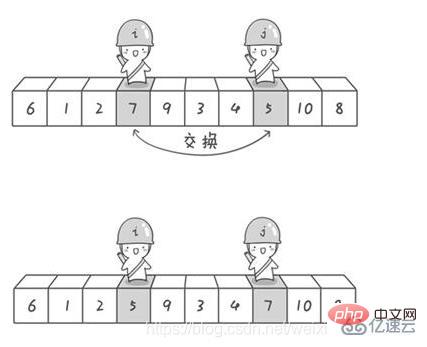
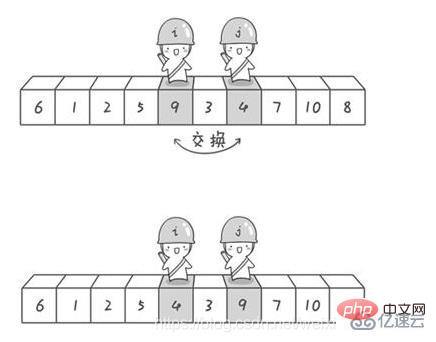
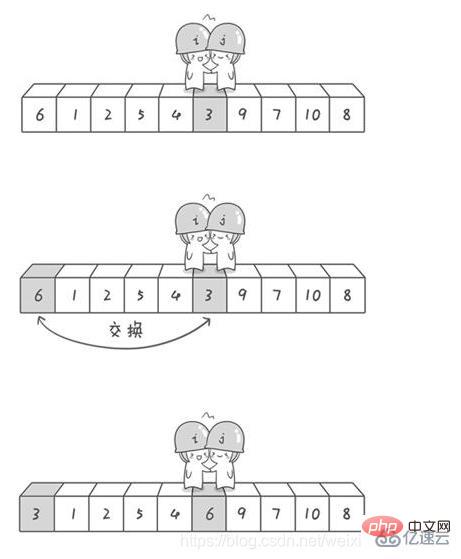
import java.util.Arrays;//快速排序：冒泡排序的升华版public class QuickSort_05 {
public static void main(String[] args) {
//int a[]={50,1,12,2};
int a[]={3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
quicksort(a,0,a.length-1);
System.out.println(Arrays.toString(a));
}
private static void quicksort(int[] a, int low, int high) {
int i,j;
if (low>high) {
return;
}
i=low;
j=high;
int temp=a[low];//基准位,low=length时，会报异常，java.lang.ArrayIndexOutOfBoundsException: 4 ，所以必须在if判断后面,就跳出方法。
while(i<j){
//先从右边开始往左递减，找到比temp小的值才停止
while ( temp<=a[j] && i<j) {
j--;
}
//再看左边开始往右递增，找到比temp大的值才停止
while ( temp>=a[i] && i<j) {
i++;
}
//满足 i<j 就交换,继续循环while(i<j)
if (i<j) {
int t=a[i];
a[i]=a[j];
a[j]=t;
}
}
//最后将基准位跟 a[i]与a[j]相等的位置，进行交换,此时i=j
a[low]=a[i];
a[i]=temp;
//左递归
quicksort(a, low, j-1);
//右递归
quicksort(a, j+1, high);
}}
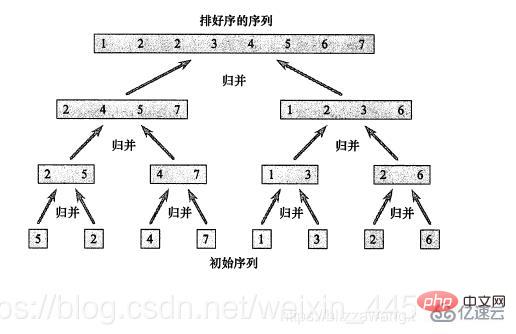
import java.util.Arrays;//归并排序public class MergeSort_06 {
public static void main(String[] args) {
int a[]={3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
//int a[]={5,2,4,7,1,3,2,2};
int temp[]=new int[a.length];
mergesort(a,0,a.length-1,temp);
System.out.println(Arrays.toString(a));
}
private static void mergesort(int[] a, int left, int right, int[] temp) {
//分解
if (left<right) {
int mid=(left+right)/2;
//向左递归进行分解
mergesort(a, left, mid, temp);
//向右递归进行分解
mergesort(a, mid+1, right, temp);
//每分解一次便合并一次
merge(a,left,right,mid,temp);
}
}
/**
*
* @param a 待排序的数组
* @param left 左边有序序列的初始索引
* @param right 右边有序序列的初始索引
* @param mid 中间索引
* @param temp 做中转的数组
*/
private static void merge(int[] a, int left, int right, int mid, int[] temp) {
int i=left; //初始i，左边有序序列的初始索引
int j=mid+1;//初始化j，右边有序序列的初始索引（右边有序序列的初始位置即中间位置的后一位置）
int t=0;//指向temp数组的当前索引，初始为0
//先把左右两边的数据（已经有序）按规则填充到temp数组
//直到左右两边的有序序列，有一边处理完成为止
while (i<=mid && j<=right) {
//如果左边有序序列的当前元素小于或等于右边的有序序列的当前元素，就将左边的元素填充到temp数组中
if (a[i]<=a[j]) {
temp[t]=a[i];
t++;//索引向后移
i++;//i后移
}else {
//反之，将右边有序序列的当前元素填充到temp数组中
temp[t]=a[j];
t++;//索引向后移
j++;//j后移
}
}
//把剩余数据的一边的元素填充到temp中
while (i<=mid) {
//此时说明左边序列还有剩余元素
//全部填充到temp数组
temp[t]=a[i];
t++;
i++;
}
while (j<=right) {
//此时说明左边序列还有剩余元素
//全部填充到temp数组
temp[t]=a[j];
t++;
j++;
}
//将temp数组的元素复制到原数组
t=0;
int tempLeft=left;
while (tempLeft<=right) {
a[tempLeft]=temp[t];
t++;
tempLeft++;
}
}
}Heap Sort
Step 1: Build the initial heap buildHeap, and use sink(arr,i, length) to adjust the value of the top of the heap;
Step 2: The purpose of sinking the top element of the heap is to float the largest element to the top of the heap, and then use sink(arr, 0,length) to adjust;
Illustration of heap sorting: link
public class Heap_Sort_07 {
public static void main(String[] args) {
int a[]={3,44,38,5,47,15,36,26,27,2,46,4,19,50,48};
sort(a);
System.out.println(Arrays.toString(a));
}
public static void sort(int[] arr) {
int length = arr.length;
//构建堆
buildHeap(arr,length);
for ( int i = length - 1; i > 0; i-- ) {
//将堆顶元素与末位元素调换
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
//数组长度-1 隐藏堆尾元素
length--;
//将堆顶元素下沉 目的是将最大的元素浮到堆顶来
sink(arr, 0,length);
}
}
private static void buildHeap(int[] arr, int length) {
for (int i = length / 2; i >= 0; i--) {
sink(arr,i, length);
}
}
private static void sink(int[] arr, int index, int length) {
int leftChild = 2 * index + 1;//左子节点下标
int rightChild = 2 * index + 2;//右子节点下标
int present = index;//要调整的节点下标
//下沉左边
if (leftChild < length && arr[leftChild] > arr[present]) {
present = leftChild;
}
//下沉右边
if (rightChild < length && arr[rightChild] > arr[present]) {
present = rightChild;
}
//如果下标不相等 证明调换过了
if (present != index) {
//交换值
int temp = arr[index];
arr[index] = arr[present];
arr[present] = temp;
//继续下沉
sink(arr, present, length);
}
}}Reference link
The steps of the algorithm are as follows:
Find the array array to be sorted The largest element max
Counts the number of occurrences of each element with a value of i in the array and stores it in the i-th item of the array count
Accumulate all counts (starting from the first element in count, adding each item to the previous item)
Fill the target array in reverse: add each element i Place it in the count [i] item of the new array. Every time an element is placed, count [i] is subtracted
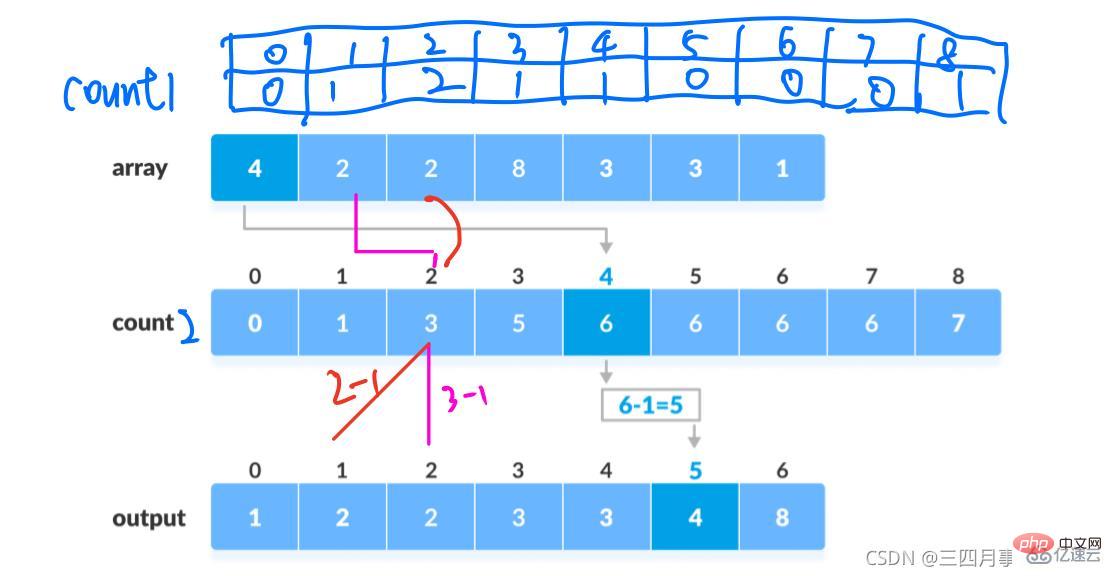
import java.util.Arrays;public class CountSort_08 {
public static void main(String[] args) {
int[] array = { 4, 2, 2, 8, 3, 3, 1 };
// 找到数组中最大的值 ---> max:8
int max = findMaxElement(array);
int[] sortedArr = countingSort(array, max + 1);
System.out.println("计数排序后的数组： " + Arrays.toString(sortedArr));
}
private static int findMaxElement(int[] array) {
int max = array[0];
for (int val : array) {
if (val > max)
max = val;
}
return max;
}
private static int[] countingSort(int[] array, int range) { //range:8+1
int[] output = new int[array.length];
int[] count = new int[range];
//初始化： count1数组
for (int i = 0; i < array.length; i++) {
count[array[i]]++;
}
//计数： count2数组，累加次数后的，这里用count2区分
for (int i = 1; i < range; i++) {
count[i] = count[i] + count[i - 1];
}
//排序：最后数组
for (int i = 0; i < array.length; i++) {
output[count[array[i]] - 1] = array[i];
count[array[i]]--;
}
return output;
}}Reference link
Bucket sort can be regarded as an upgraded version of counting sort. It divides the data to be sorted into multiple ordered buckets. The data is then sorted separately, and the data from each bucket is taken out in turn to complete the sorting.
Bucket sorting: Put the element with value i into bucket i, and finally pour out the elements in the bucket in sequence. 
Bucket sorting sequence idea:
Set a quantitative array as an empty bucket.
Search the sequence and put the items into the corresponding buckets one by one.
Sort each bucket that is not empty.
Put items from the bucket that are not empty back into the original sequence.
public class BucketSort_09 {
public static void sort(int[] arr){
//最大最小值
int max = arr[0];
int min = arr[0];
int length = arr.length;
for(int i=1; i<length; i++) {
if(arr[i] > max) {
max = arr[i];
} else if(arr[i] < min) {
min = arr[i];
}
}
//最大值和最小值的差
int diff = max - min;
//桶列表
ArrayList<ArrayList<Integer>> bucketList = new ArrayList<>();
for(int i = 0; i < length; i++){
bucketList.add(new ArrayList<>());
}
//每个桶的存数区间
float section = (float) diff / (float) (length - 1);
//数据入桶
for(int i = 0; i < length; i++){
//当前数除以区间得出存放桶的位置 减1后得出桶的下标
int num = (int) (arr[i] / section) - 1;
if(num < 0){
num = 0;
}
bucketList.get(num).add(arr[i]);
}
//桶内排序
for(int i = 0; i < bucketList.size(); i++){
//jdk的排序速度当然信得过
Collections.sort(bucketList.get(i));
}
//写入原数组
int index = 0;
for(ArrayList<Integer> arrayList : bucketList){
for(int value : arrayList){
arr[index] = value;
index++;
}
}
}}We assume that there is an array to be sorted [53, 3, 542, 748, 14, 214], then how What about sorting it using radix sort?
First we have ten one-dimensional arrays like this, also called buckets in radix sorting. Implemented using bucket sort. 
In the first round, distinguish by the single digit of the element: [542, 53, 3, 14, 214,748]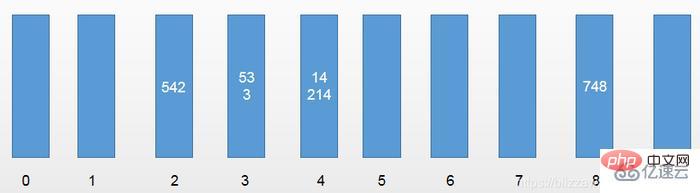
Second Round, distinguished by the tens digit of the element: [3, 14, 214, 542, 748, 53]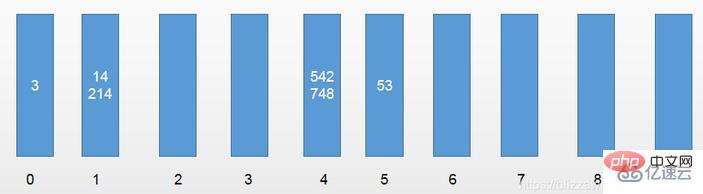 
The third round, distinguished by the hundreds digit of the element: [3, 14 , 53, 214, 542, 748]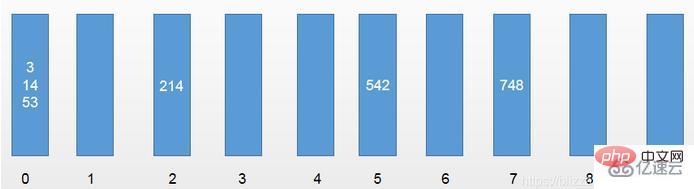
import java.util.Arrays;public class RaixSort_10 {
public static void main(String[] args) {
int[] arr = { 53, 3, 542, 748, 14, 214 };
// 得到数组中最大的数
int max = arr[0];// 假设第一个数就是数组中的最大数
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
// 得到最大数是几位数
// 通过拼接一个空串将其变为字符串进而求得字符串的长度，即为位数
int maxLength = (max + "").length();
// 定义一个二维数组，模拟桶，每个桶就是一个一维数组
// 为了防止放入数据的时候桶溢出，我们应该尽量将桶的容量设置得大一些
int[][] bucket = new int[10][arr.length];
// 记录每个桶中实际存放的元素个数
// 定义一个一维数组来记录每个桶中每次放入的元素个数
int[] bucketElementCounts = new int[10];
// 通过变量n帮助取出元素位数上的数
for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {
for (int j = 0; j < arr.length; j++) {
// 针对每个元素的位数进行处理
int digitOfElement = arr[j] / n % 10;
// 将元素放入对应的桶中
// bucketElementCounts[digitOfElement]就是桶中的元素个数，初始为0，放在第一位
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
// 将桶中的元素个数++
// 这样接下来的元素就可以排在前面的元素后面
bucketElementCounts[digitOfElement]++;
}
// 按照桶的顺序取出数据并放回原数组
int index = 0;
for (int k = 0; k < bucket.length; k++) {
// 如果桶中有数据，才取出放回原数组
if (bucketElementCounts[k] != 0) {
// 说明桶中有数据，对该桶进行遍历
for (int l = 0; l < bucketElementCounts[k]; l++) {
// 取出元素放回原数组
arr[index++] = bucket[k][l];
}
}
// 每轮处理后，需要将每个bucketElementCounts[k]置0
bucketElementCounts[k] = 0;
}
}
System.out.println(Arrays.toString(arr));//[3, 14, 53, 214, 542, 748]
}}Radix sorting is a classic algorithm that trades space for time. When there is enough data, the memory space may reach tens of millions. Not enough, heap memory overflow occurred
The above is the detailed content of What are the sorting algorithms in java. For more information, please follow other related articles on the PHP Chinese website!
![[Web front-end] Node.js quick start](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
