How to implement graph traversal in Java

1. Graph traversal

Start from a certain vertex in the graph and visit the remaining vertices in the graph, and each vertex is only visited once

There are two types of depth-first traversal in graph traversal DFS, breadth-first traversal BFS

2. Depth-first traversal

Depth-first traversal traverses with depth first, which simply means going to the end every time. Similar to the pre-order traversal of a binary tree

Ideas:

1. Perform a depth-first traversal starting from a certain vertex, and mark the vertex as visited

2. Take the With the vertex as the starting point, select any path and traverse to the end, and mark the visited vertices

3. In step 2, traverse to the end and go back to the previous vertex, and repeat step 2

4. End of traversing all vertices

According to the traversal idea, this is a recursive process. In fact, DFS is basically the same as backtracking.

Traversal:

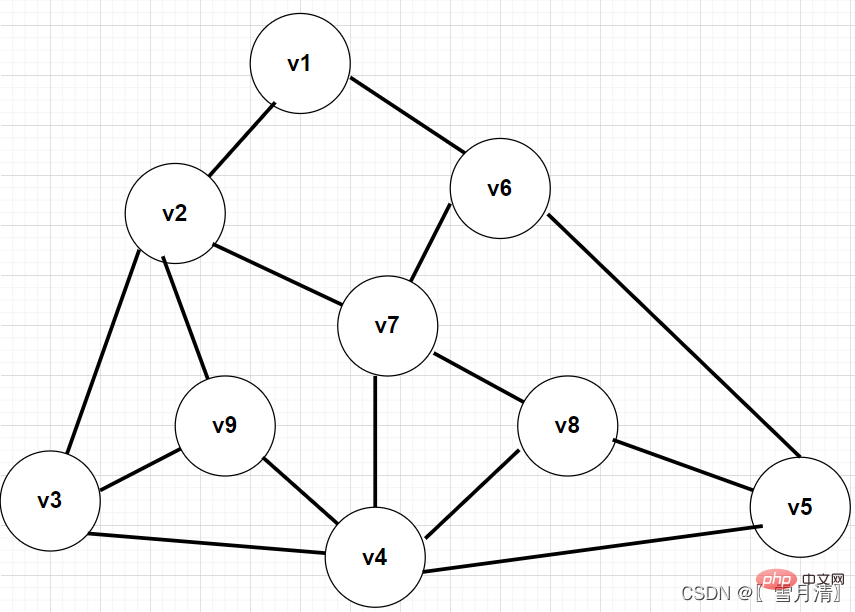
Take this picture as an example to perform depth-first traversal

	static void dfs(int[][] graph,int idx,boolean[]visit) {
		int len = graph.length;
		//访问过
	 if(visit[idx]) return;
	 //访问该顶点
	 System.out.println("V"+idx);
	 //标志顶点
	 visit[idx] = true;
	 for(int i = 1;i < len;i++) {
	 //访问该顶点相连的所有边
		 if(graph[idx][i] == 1) {
	 //递归进行dfs遍历
		 dfs(graph, i, visit);
		 }
	 }
			
	}

Traversal result:

V1

V2

V3

#V4

V5

V6

V7

V8

V9

Code to create the graph:

public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();
		
		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			graph[v2][v1] = 1;
		}
		
		//标记数组 false表示未访问过 
		boolean[] visit = new boolean[n+1];
		dfs(graph, 1, visit);
		
	}

3. Use DFS to determine whether there is a cycle in the directed graph

Idea: Traverse a certain A vertex, if in addition to the previous vertex, there are other connected vertices that have been visited, then there must be a cycle

	//默认无环
   static boolean flag = false;
	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();
		
		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			
		}
	 //标记数组 true为访问过
		boolean[] visit = new boolean[n+1];
		dfs(graph, 1, visit,1);
		if(flag) 
			System.out.println("有环");
		
	}
	
	static void dfs(int[][] graph,int idx,boolean[]visit,int parent) {
		int len = graph.length;
	
	 System.out.println("V"+idx);
	 //标记顶点
	 visit[idx] = true;
	 for(int i = 1;i < len;i++) {
		 //访问该顶点相连的所有边
		 if(graph[idx][i] == 1) {
		 if( !visit[i] ) {
		 dfs(graph, i, visit,idx);
		 }
		 else if(idx != i) {
			 flag = true;
		 }
		 }
	 }
	
	 
	}

Note: It is a directed graph to determine whether there is a cycle, and an undirected graph to determine whether there is a cycle Whether there is a cycle is meaningless, because the vertices of any two existing paths can be cycles

4. Breadth-first traversal

Breadth-first traversal is performed with breadth (width) as priority traverse. Similar to the level-order traversal of a binary tree

Ideas:

1. Take a certain vertex as the starting point for breadth-first traversal, and mark the vertex as visited

2.Visit all Vertices that are connected to the vertex and have not been visited, and mark the visited vertices

3. Repeat steps 1 and 2 starting from the vertices visited in step 2

4.Traverse all Vertex end

The traversal is assisted by the queue, and the queue queuing order is the breadth-first traversal result

Traversal

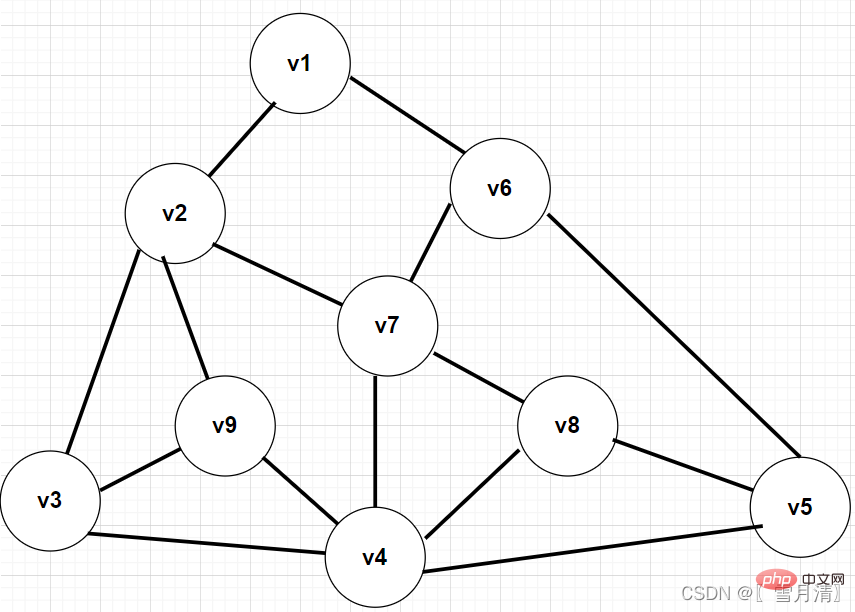
Take this picture as an example, use the adjacency matrix method to create the graph, and perform BFS traversal

	static void bfs(int[][] graph) {		
		int len = graph.length;
		//标记数组 false表示未访问过 
		boolean[] visit = new boolean[len];
		//辅助队列
		Queue<Integer> queue = new LinkedList<>();
		
		queue.offer(1);
		visit[1] = true;
		
		while(!queue.isEmpty()) {
			int num = queue.poll();
			System.out.println("V"+num);
					
			//遍历该顶点所有相连顶点
			for(int i = 1;i < len;i++) {
				//相连并且没有被访问过
				if(graph[num][i] == 1 && !visit[i]) {
					queue.offer(i);
					visit[i] = true;				
				}
			}
		}	
	}

Traversal results:

V1

V2

V6

V3

V7

V9

V5

V4

V8

Code to create graph

public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		//顶点数 以1开始
		int n = scanner.nextInt();
		int[][] graph = new int[n+1][n+1];
		//边数
		int m = scanner.nextInt();
		
		for(int i = 1;i <= m;i++) {
			int v1 = scanner.nextInt();
			int v2 = scanner.nextInt();
			graph[v1][v2] = 1;
			graph[v2][v1] = 1;
		}
		bfs(graph);
	}

The above is the detailed content of How to implement graph traversal in Java. For more information, please follow other related articles on the PHP Chinese website!