Example analysis of hash table in Java
1, concept
In the sequential structure and balanced tree, there is no corresponding relationship between the element key code and its storage location, so when searching for an element , must go through multiple comparisons of key codes. The time complexity of sequential search is O(N). In a balanced tree, it is the height of the tree, that is, O( ). The efficiency of the search depends on the number of comparisons of elements during the search process.
Ideal search method: you can get the elements to be searched directly from the table at one time without any comparison. If you construct a storage structure and use a certain function (hashFunc) to establish a one-to-one mapping relationship between the storage location of the element and its key code, then the element can be found quickly through this function during search.
When inserting an element into this structure:
According to the key code of the element to be inserted, this function calculates the storage location of the element and stores it according to this location.
Search for elements
Perform the same calculation on the key code of the element, treat the obtained function value as the storage location of the element, and compare the elements according to this location in the structure. If the key codes are equal , the search is successful
For example: data set {1, 7, 6, 4, 5, 9};
The hash function is set to: hash(key) = key % capacity; capacity It is the total size of the underlying space for storing elements.
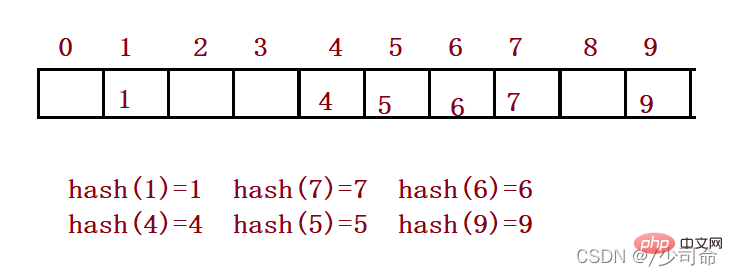 2, conflict-avoidance
2, conflict-avoidance
First of all, we need to make it clear that because the capacity of the underlying array of our hash table is often smaller than the actual key to be stored The number of words causes a problem. The occurrence of conflicts is inevitable, but what we can do is to reduce the conflict rate as much as possible.
3, conflict-avoidance-hash function design
Common hash functions
Direct customization method--(commonly used)
take keywords A certain linear function is a hash address: Hash (Key) = A*Key B Advantages: Simple and uniform Disadvantages: Need to know the distribution of keywords in advance Usage scenario: Suitable for finding relatively small and continuous situations
Division with remainder method--(commonly used)
Suppose the number of addresses allowed in the hash table is m, take a prime number p that is not greater than m, but is closest to or equal to m as the divisor, according to the hash function: Hash (key) = key% p(p
Squaring the middle method--(understand)
Assume the key is 1234, for Its square is 1522756, and the middle three digits 227 are extracted as the hash address; another example is the keyword 4321, and its square is 18671041, and the middle three digits 671 (or 710) are extracted as the hash address. The square method is more suitable: The distribution of keywords is not known, and the number of bits is not very large
4, conflict-avoidance-load factor adjustment
 Load factor and conflict Rough demonstration of the relationship between rates
Load factor and conflict Rough demonstration of the relationship between rates
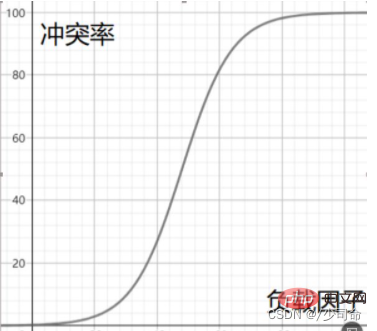 #So when the conflict rate reaches an intolerable level, we need to reduce the conflict rate in disguise by reducing the load factor. , It is known that the number of keywords in the hash table is immutable, then all we can adjust is the size of the array in the hash table.
#So when the conflict rate reaches an intolerable level, we need to reduce the conflict rate in disguise by reducing the load factor. , It is known that the number of keywords in the hash table is immutable, then all we can adjust is the size of the array in the hash table.
5, Conflict-Resolution-Closed Hash
Closed hash: also called open addressing method. When a hash conflict occurs, if the hash table is not full, it means that the hash table is not full. There must be an empty position in the Greek table, so the key can be stored in the "next" empty position in the conflicting position.
①Linear Detection
For example, in the above scenario, you now need to insert element 44. First, calculate the hash address through the hash function. The subscript is 4, so 44 should theoretically be inserted at this position. , but an element with a value of 4 is already placed at this position, that is, a hash conflict occurs. Linear detection: Starting from the position where the conflict occurs, detect backwards until the next empty position is found.
Insert
Get the position of the element to be inserted in the hash table through the hash function. If there is no element in the position, insert the new element directly. If there is an element in the position, a hash conflict occurs. , use linear detection to find the next empty position, and insert new elements
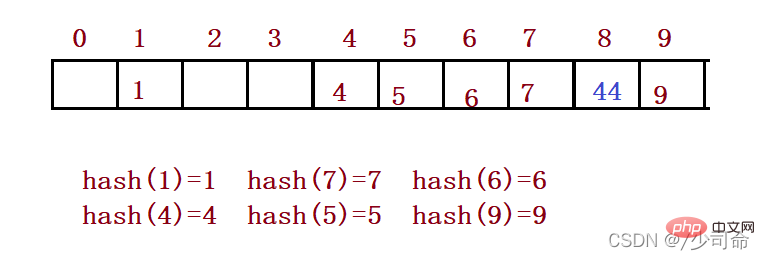 When using closed hashing to handle hash conflicts, you cannot physically delete existing elements in the hash table. , if you delete the element directly, it will affect the search of other elements. For example, if you delete element 4 directly, the search for 44 may be affected. Therefore linear probing uses marked pseudo-deletion to delete an element.
When using closed hashing to handle hash conflicts, you cannot physically delete existing elements in the hash table. , if you delete the element directly, it will affect the search of other elements. For example, if you delete element 4 directly, the search for 44 may be affected. Therefore linear probing uses marked pseudo-deletion to delete an element.
②Second Detection
The flaw of linear detection is that conflicting data accumulates together, which is related to finding the next empty position, because the way to find empty positions is to find them one by one. , so in order to avoid this problem in secondary detection, the method to find the next empty position is: = ( )% m, or: = ( - )% m. Among them: i = 1,2,3..., is the position calculated by the hash function Hash(x) on the key code of the element, and m is the size of the table. For 2.1, if you want to insert 44, a conflict occurs. The situation after using the solution is:

Research shows that when the length of the table is a prime number and the table loading factor a does not exceed 0.5 , new entries will definitely be inserted, and no position will be probed twice. Therefore, as long as there are half empty positions in the table, there will be no table full problem. When searching, you do not need to consider that the table is full, but when inserting, you must ensure that the load factor a of the table does not exceed 0.5. If it exceeds, you must consider increasing the capacity.
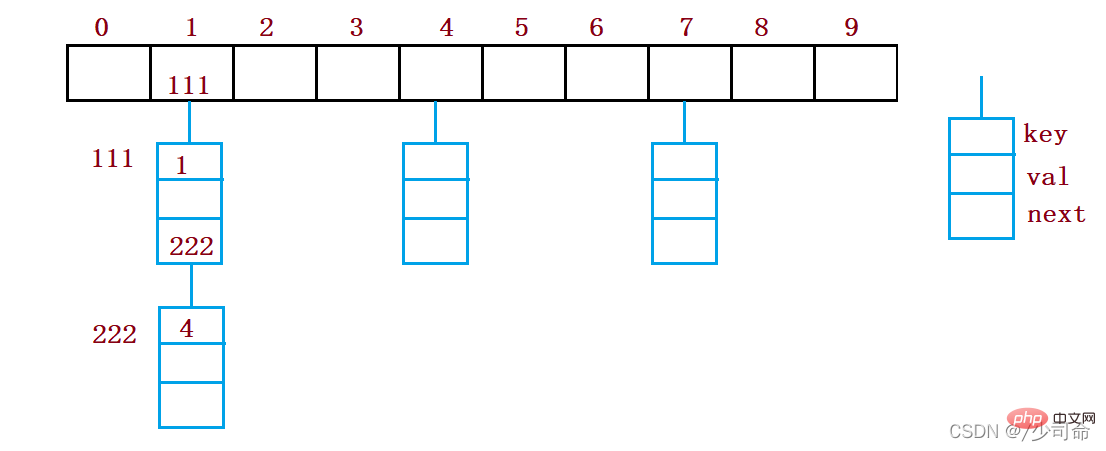
6, Conflict-Resolution-Open Hash/Hash Bucket
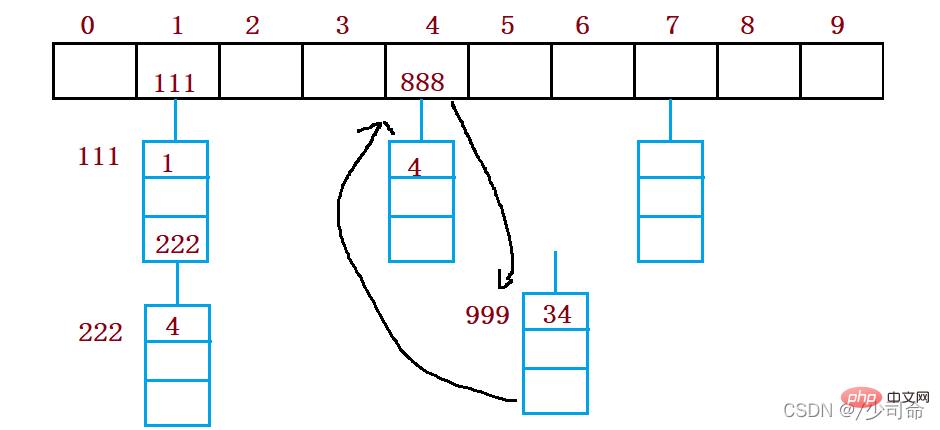
The open hash method is also called the chain address method (open chain method). First, the hash function is used to calculate the key code set. Hash address. Key codes with the same address belong to the same sub-set. Each sub-set is called a bucket. The elements in each bucket are linked through a singly linked list. The head node of each linked list is stored in the hash table.

static class Node {
public int key;
public int val;
public Node next;
public Node(int key, int val) {
this.key = key;
this.val = val;
}
}
private Node[] array;
public int usedSize;
public HashBucket() {
this.array = new Node[10];
this.usedSize = 0;
}
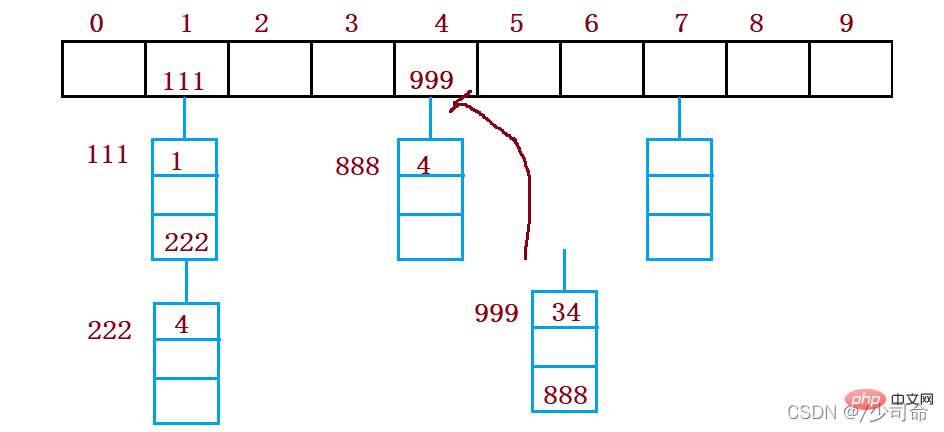 ##
##
public void put(int key,int val){
int index = key % this.array.length;
Node cur = array[index];
while (cur != null){
if(cur.val == key){
cur.val = val;
return;
}
cur = cur.next;
}
//头插法
Node node = new Node(key,val);
node.next = array[index];
array[index] = node;
this.usedSize++;
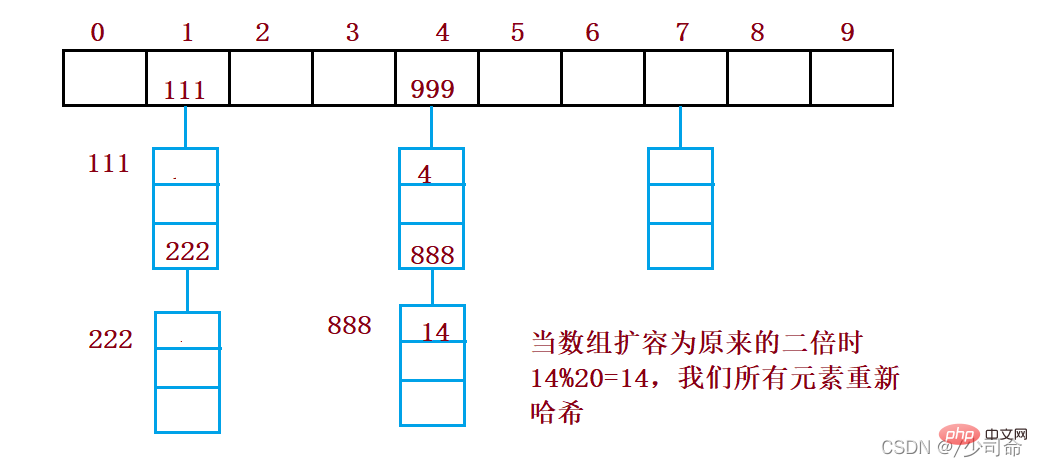
if(loadFactor() >= 0.75){
resize();
}
}
public int get(int key) {
//以什么方式存储的 那就以什么方式取
int index = key % this.array.length;
Node cur = array[index];
while (cur != null) {
if(cur.key == key) {
return cur.val;
}
cur = cur.next;
}
return -1;//
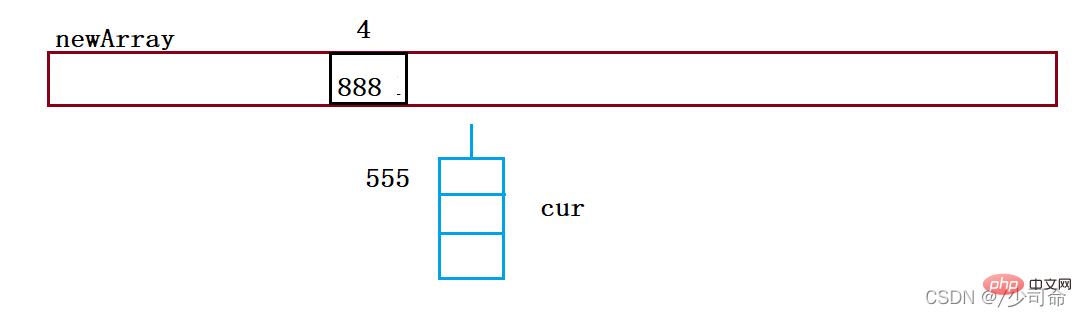
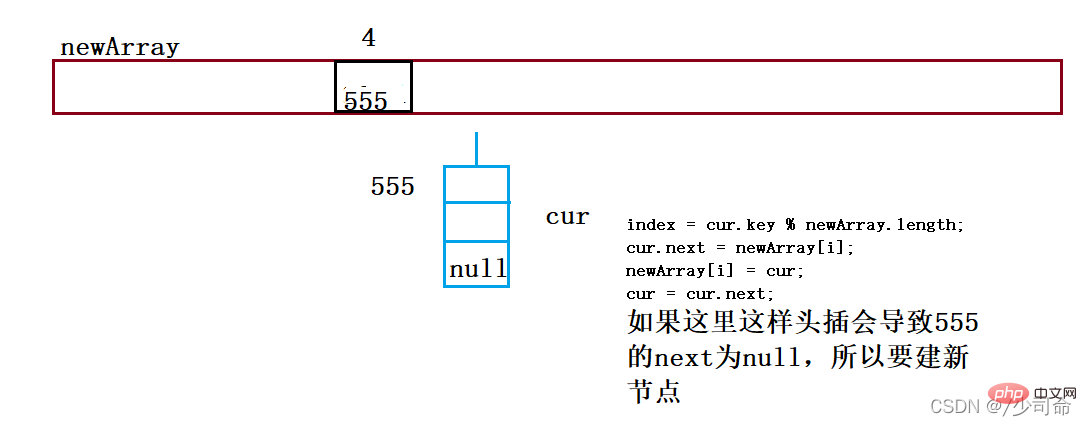
}public void resize(){
Node[] newArray = new Node[2*this.array.length];
for (int i = 0; i < this.array.length; i++){
Node cur = array[i];
Node curNext = null;
while (cur != null){
curNext = cur.next;
int index = cur.key % newArray.length;
cur.next = newArray[i];
newArray[i] = cur;
cur = curNext.next;
cur = curNext;
}
}
this.array = newArray;
}Copy after login
public void resize(){
Node[] newArray = new Node[2*this.array.length];
for (int i = 0; i < this.array.length; i++){
Node cur = array[i];
Node curNext = null;
while (cur != null){
curNext = cur.next;
int index = cur.key % newArray.length;
cur.next = newArray[i];
newArray[i] = cur;
cur = curNext.next;
cur = curNext;
}
}
this.array = newArray;
}The above is the detailed content of Example analysis of hash table in Java. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1392
1392
 52
52
 Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Perfect Number in Java. Here we discuss the Definition, How to check Perfect number in Java?, examples with code implementation.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Guide to Weka in Java. Here we discuss the Introduction, how to use weka java, the type of platform, and advantages with examples.
 Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Smith Number in Java. Here we discuss the Definition, How to check smith number in Java? example with code implementation.
 Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
In this article, we have kept the most asked Java Spring Interview Questions with their detailed answers. So that you can crack the interview.
 Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Java 8 introduces the Stream API, providing a powerful and expressive way to process data collections. However, a common question when using Stream is: How to break or return from a forEach operation? Traditional loops allow for early interruption or return, but Stream's forEach method does not directly support this method. This article will explain the reasons and explore alternative methods for implementing premature termination in Stream processing systems. Further reading: Java Stream API improvements Understand Stream forEach The forEach method is a terminal operation that performs one operation on each element in the Stream. Its design intention is
 TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
Guide to TimeStamp to Date in Java. Here we also discuss the introduction and how to convert timestamp to date in java along with examples.
 Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Capsules are three-dimensional geometric figures, composed of a cylinder and a hemisphere at both ends. The volume of the capsule can be calculated by adding the volume of the cylinder and the volume of the hemisphere at both ends. This tutorial will discuss how to calculate the volume of a given capsule in Java using different methods. Capsule volume formula The formula for capsule volume is as follows: Capsule volume = Cylindrical volume Volume Two hemisphere volume in, r: The radius of the hemisphere. h: The height of the cylinder (excluding the hemisphere). Example 1 enter Radius = 5 units Height = 10 units Output Volume = 1570.8 cubic units explain Calculate volume using formula: Volume = π × r2 × h (4
 Create the Future: Java Programming for Absolute Beginners
Oct 13, 2024 pm 01:32 PM
Create the Future: Java Programming for Absolute Beginners
Oct 13, 2024 pm 01:32 PM
Java is a popular programming language that can be learned by both beginners and experienced developers. This tutorial starts with basic concepts and progresses through advanced topics. After installing the Java Development Kit, you can practice programming by creating a simple "Hello, World!" program. After you understand the code, use the command prompt to compile and run the program, and "Hello, World!" will be output on the console. Learning Java starts your programming journey, and as your mastery deepens, you can create more complex applications.




