Java binary search tree example analysis
Concept
Binary search tree is also called binary sorting tree. It is either an empty tree or has the following properties Binary tree:
1. If its left subtree is not empty, then the values of all nodes on the left subtree are less than the value of the root node.
2. If its right subtree is not empty, the values of all nodes on the right subtree are greater than the value of the root node.
3. Its left and right subtrees are also binary search trees respectively
Direct practice
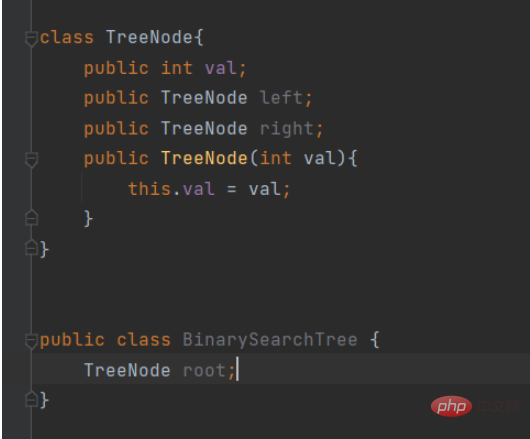
Preparation work: define a class of tree nodes, and binary search tree classes.
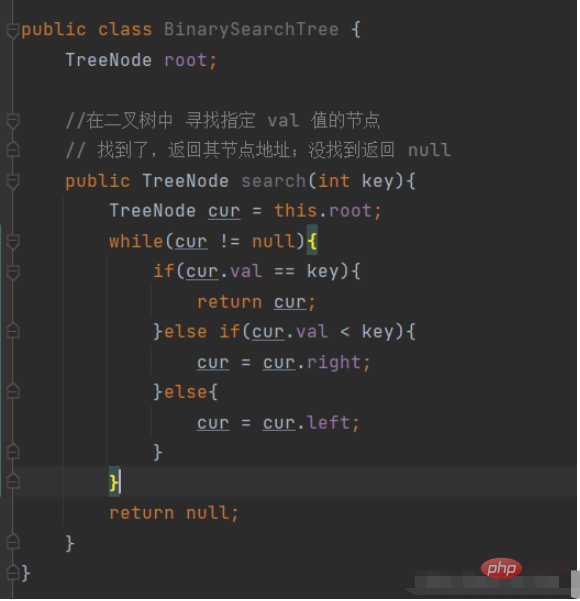
Search function of binary tree
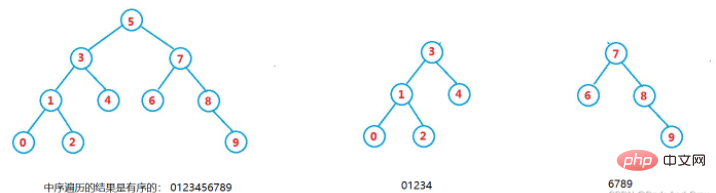
Assume that we have constructed such a binary tree, as shown below
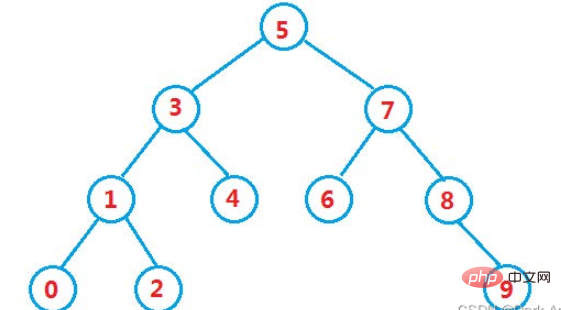
The first question we have to think about is how to find whether a certain value is in the binary tree?
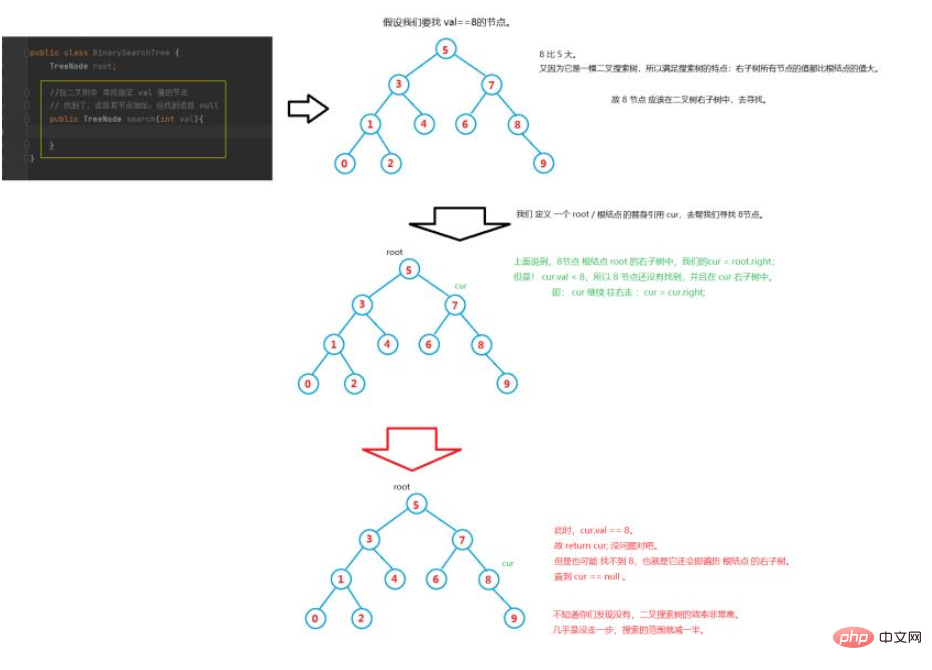
According to the above logic, let’s search method Make improvements.
Insertion operation of searching binary tree
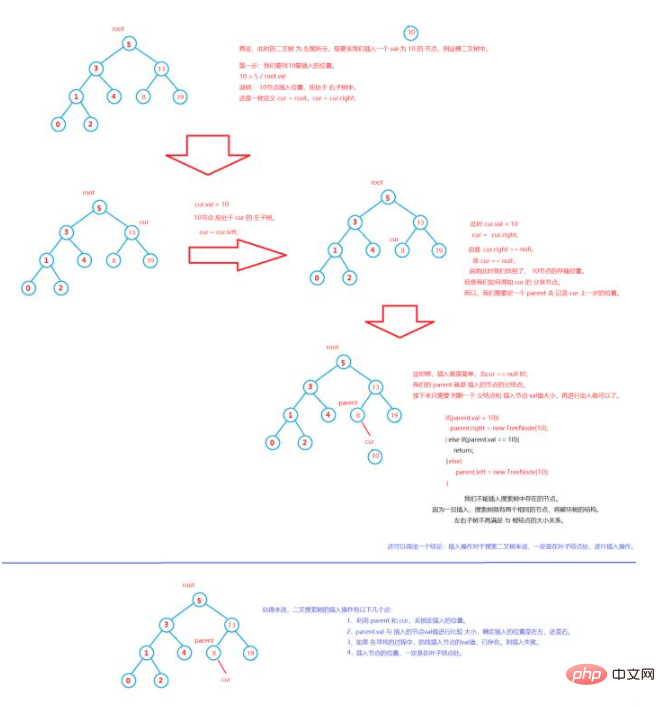
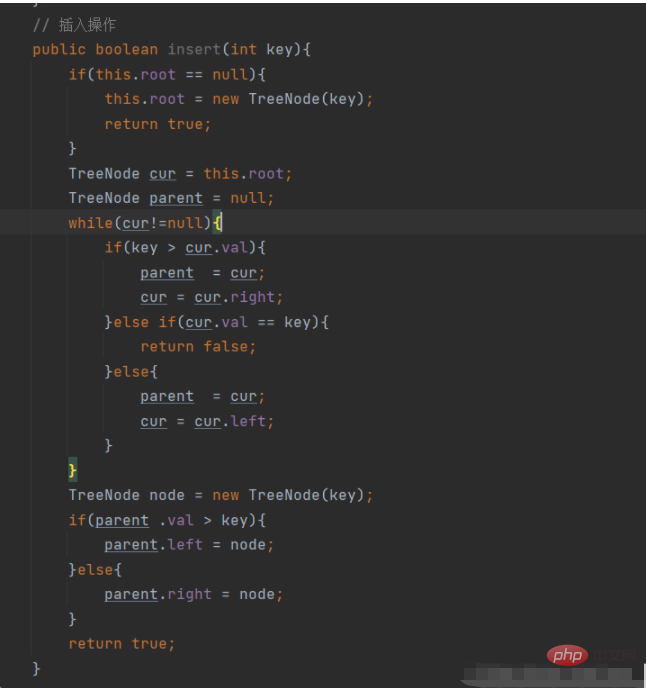
Based on the above logic, let’s write a code to insert a node.
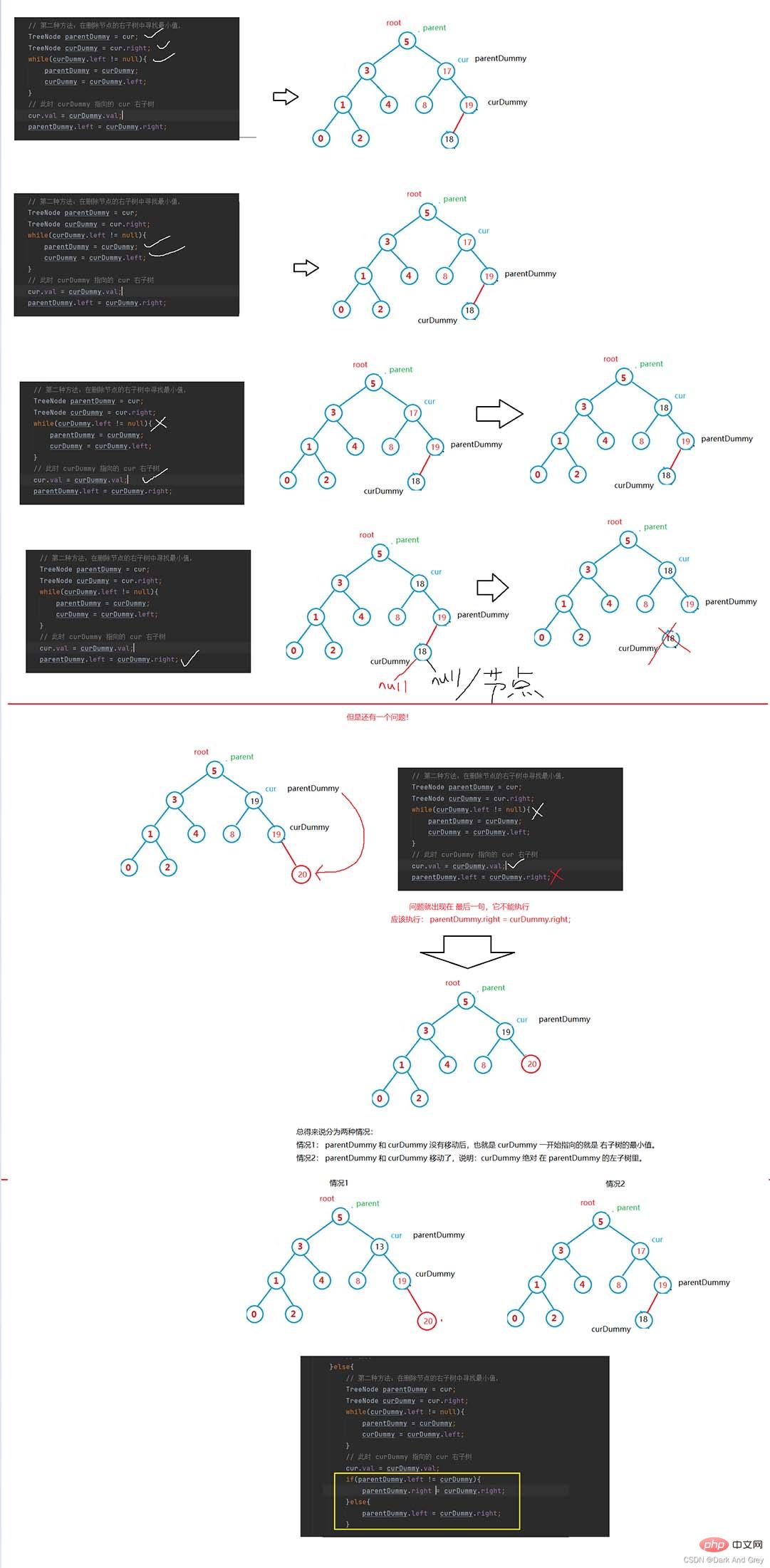
Operation of searching binary tree to delete nodes-difficulty
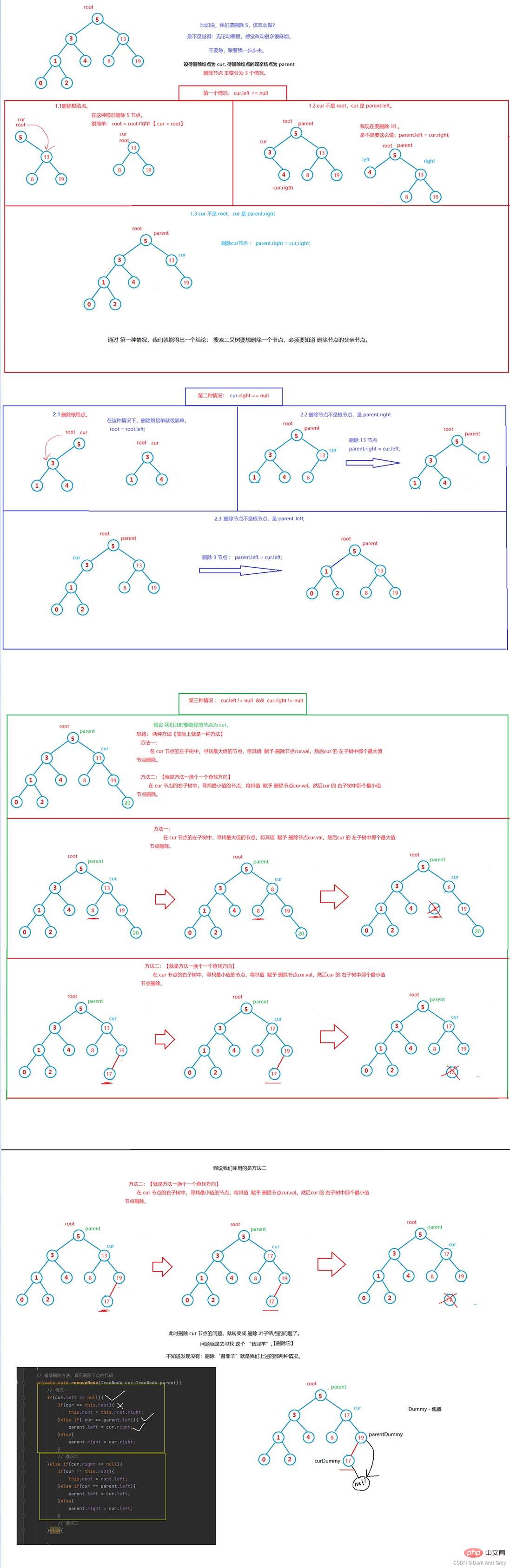
Let’s analyze again: how curDummy and parentDummy find the “scapegoat” "of.
Total Program - Simulation to Implement Binary Search Tree
class TreeNode{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val){
this.val = val;
}
}
public class BinarySearchTree {
TreeNode root;
//在二叉树中 寻找指定 val 值的节点
// 找到了,返回其节点地址;没找到返回 null
public TreeNode search(int key){
TreeNode cur = this.root;
while(cur != null){
if(cur.val == key){
return cur;
}else if(cur.val < key){
cur = cur.right;
}else{
cur = cur.left;
}
}
return null;
}
// 插入操作
public boolean insert(int key){
if(this.root == null){
this.root = new TreeNode(key);
return true;
}
TreeNode cur = this.root;
TreeNode parent = null;
while(cur!=null){
if(key > cur.val){
parent = cur;
cur = cur.right;
}else if(cur.val == key){
return false;
}else{
parent = cur;
cur = cur.left;
}
}
TreeNode node = new TreeNode(key);
if(parent .val > key){
parent.left = node;
}else{
parent.right = node;
}
return true;
}
// 删除操作
public void remove(int key){
TreeNode cur = root;
TreeNode parent = null;
// 寻找 删除节点位置。
while(cur!=null){
if(cur.val == key){
removeNode(cur,parent);// 真正删除节点的代码
break;
}else if(cur.val < key){
parent = cur;
cur = cur.right;
}else{
parent = cur;
cur = cur.left;
}
}
}
// 辅助删除方法:真正删除节点的代码
private void removeNode(TreeNode cur,TreeNode parent){
// 情况一
if(cur.left == null){
if(cur == this.root){
this.root = this.root.right;
}else if( cur == parent.left){
parent.left = cur.right;
}else{
parent.right = cur.right;
}
// 情况二
}else if(cur.right == null){
if(cur == this.root){
this.root = root.left;
}else if(cur == parent.left){
parent.left = cur.left;
}else{
parent.right = cur.left;
}
// 情况三
}else{
// 第二种方法:在删除节点的右子树中寻找最小值,
TreeNode parentDummy = cur;
TreeNode curDummy = cur.right;
while(curDummy.left != null){
parentDummy = curDummy;
curDummy = curDummy.left;
}
// 此时 curDummy 指向的 cur 右子树
cur.val = curDummy.val;
if(parentDummy.left != curDummy){
parentDummy.right = curDummy.right;
}else{
parentDummy.left = curDummy.right;
}
}
}
// 中序遍历
public void inorder(TreeNode root){
if(root == null){
return;
}
inorder(root.left);
System.out.print(root.val+" ");
inorder(root.right);
}
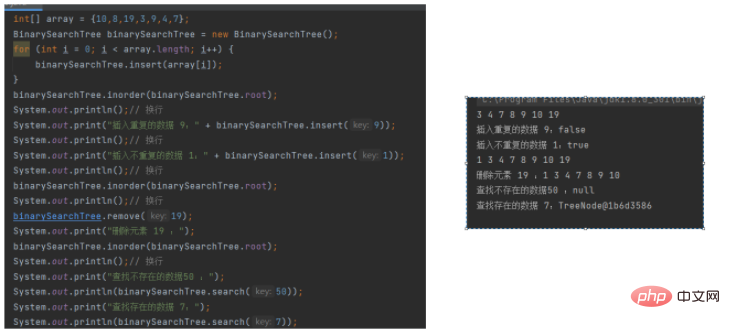
public static void main(String[] args) {
int[] array = {10,8,19,3,9,4,7};
BinarySearchTree binarySearchTree = new BinarySearchTree();
for (int i = 0; i < array.length; i++) {
binarySearchTree.insert(array[i]);
}
binarySearchTree.inorder(binarySearchTree.root);
System.out.println();// 换行
System.out.print("插入重复的数据 9:" + binarySearchTree.insert(9));
System.out.println();// 换行
System.out.print("插入不重复的数据 1:" + binarySearchTree.insert(1));
System.out.println();// 换行
binarySearchTree.inorder(binarySearchTree.root);
System.out.println();// 换行
binarySearchTree.remove(19);
System.out.print("删除元素 19 :");
binarySearchTree.inorder(binarySearchTree.root);
System.out.println();// 换行
System.out.print("查找不存在的数据50 :");
System.out.println(binarySearchTree.search(50));
System.out.print("查找存在的数据 7:");
System.out.println(binarySearchTree.search(7));
}
}
Performance Analysis
Insertion and deletion operations must be searched first. Search efficiency represents the performance of each operation in the binary search tree.
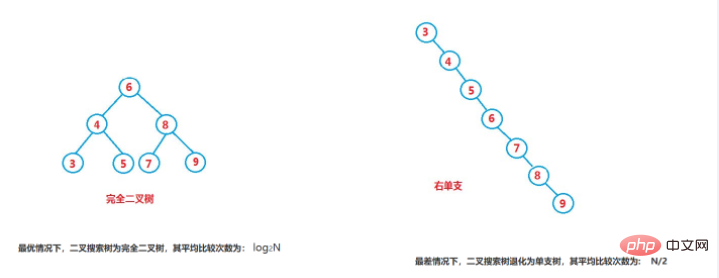
For a binary search tree with n nodes, if the probability of searching for each element is equal, the average search length of the binary search tree is the number of nodes in the binary search tree A function of depth, that is, the deeper the node, the more comparisons it takes.
But for the same key code set, if the key codes are inserted in a different order, binary search trees with different structures may be obtained:If we can ensure that the height difference between the left and right subtrees of the binary search tree does not exceed 1. Try to meet the high balance conditions.
This becomes an AVL tree (highly balanced binary search tree). The AVL tree also has disadvantages: it requires frequent rotation. A lot of wasted efficiency.
At this point, the red-black tree is born to avoid more rotations.
Relationship with java class sets
TreeMap and TreeSet are Map and Set implemented using search trees in java; in fact, red-black trees are used, and red The black tree is an approximately balanced binary search tree, that is, based on the binary search tree, the color and red-black tree properties are verified. Regarding the content of the red-black tree, bloggers will write blogs after learning it.
The above is the detailed content of Java binary search tree example analysis. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
 Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Perfect Number in Java. Here we discuss the Definition, How to check Perfect number in Java?, examples with code implementation.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Guide to Weka in Java. Here we discuss the Introduction, how to use weka java, the type of platform, and advantages with examples.
 Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Smith Number in Java. Here we discuss the Definition, How to check smith number in Java? example with code implementation.
 Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
In this article, we have kept the most asked Java Spring Interview Questions with their detailed answers. So that you can crack the interview.
 Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Java 8 introduces the Stream API, providing a powerful and expressive way to process data collections. However, a common question when using Stream is: How to break or return from a forEach operation? Traditional loops allow for early interruption or return, but Stream's forEach method does not directly support this method. This article will explain the reasons and explore alternative methods for implementing premature termination in Stream processing systems. Further reading: Java Stream API improvements Understand Stream forEach The forEach method is a terminal operation that performs one operation on each element in the Stream. Its design intention is
 TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
Guide to TimeStamp to Date in Java. Here we also discuss the introduction and how to convert timestamp to date in java along with examples.
 Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Capsules are three-dimensional geometric figures, composed of a cylinder and a hemisphere at both ends. The volume of the capsule can be calculated by adding the volume of the cylinder and the volume of the hemisphere at both ends. This tutorial will discuss how to calculate the volume of a given capsule in Java using different methods. Capsule volume formula The formula for capsule volume is as follows: Capsule volume = Cylindrical volume Volume Two hemisphere volume in, r: The radius of the hemisphere. h: The height of the cylinder (excluding the hemisphere). Example 1 enter Radius = 5 units Height = 10 units Output Volume = 1570.8 cubic units explain Calculate volume using formula: Volume = π × r2 × h (4
 Create the Future: Java Programming for Absolute Beginners
Oct 13, 2024 pm 01:32 PM
Create the Future: Java Programming for Absolute Beginners
Oct 13, 2024 pm 01:32 PM
Java is a popular programming language that can be learned by both beginners and experienced developers. This tutorial starts with basic concepts and progresses through advanced topics. After installing the Java Development Kit, you can practice programming by creating a simple "Hello, World!" program. After you understand the code, use the command prompt to compile and run the program, and "Hello, World!" will be output on the console. Learning Java starts your programming journey, and as your mastery deepens, you can create more complex applications.