How to implement softmax backpropagation in Python.

Backpropagation derivation

As you can see, softmax calculates the inputs of multiple neurons. When deriving backpropagation, you need to consider deriving the parameters of different neurons.

Consider two situations:

• When the parameter for derivation is located in the numerator

• When the parameter for derivation is located at When the denominator is

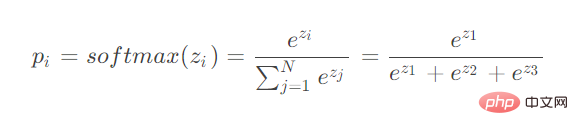
When the parameter for derivation is in the numerator:

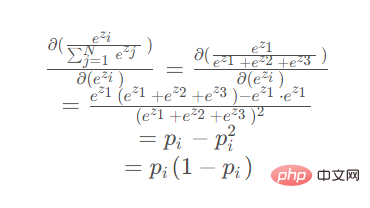
When derivation When the parameter is in the denominator (e^z2 or e^z3 are symmetrical, the derivation results are the same):

code

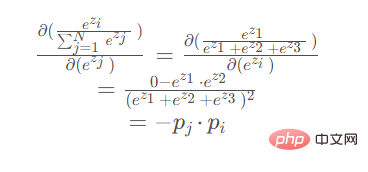
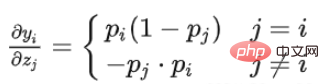
import torch
import math

def my_softmax(features):
    _sum = 0
    for i in features:
        _sum += math.e ** i
    return torch.Tensor([ math.e ** i / _sum for i in features ])

def my_softmax_grad(outputs):    
    n = len(outputs)
    grad = []
    for i in range(n):
        temp = []
        for j in range(n):
            if i == j:
                temp.append(outputs[i] * (1- outputs[i]))
            else:
                temp.append(-outputs[j] * outputs[i])
        grad.append(torch.Tensor(temp))
    return grad

if __name__ == '__main__':

    features = torch.randn(10)
    features.requires_grad_()

    torch_softmax = torch.nn.functional.softmax
    p1 = torch_softmax(features,dim=0)
    p2 = my_softmax(features)
    print(torch.allclose(p1,p2))
    
    n = len(p1)
    p2_grad = my_softmax_grad(p2)
    for i in range(n):
        p1_grad = torch.autograd.grad(p1[i],features, retain_graph=True)
        print(torch.allclose(p1_grad[0], p2_grad[i]))

The above is the detailed content of How to implement softmax backpropagation in Python.. For more information, please follow other related articles on the PHP Chinese website!