How to use Python to find the norm and determinant of a matrix

In the function of scipy.linalg, two parameters are often provided. One is check_finite. When it is True, a limited check will be performed. The other type is overwrite_xxxx, which indicates whether xxxx can be overwritten during the calculation process. For the sake of simplicity, it will be said later that a provides an overwrite switch, which means there is a parameter overwrite_a. When it is True, a is allowed to be overwritten during the calculation process; If a limited check switch is provided, it means that the check_finite parameter is provided.

Norm

The function norm is provided in scipy.linalg to find the norm, which is defined as

norm(a, ord=None, axis=None, keepdims=False, check_finite=True)

Whereord is used to declare the order of the norm

##ordMatrix normVector norm #None'fro' ##'nuc'-##max(sum(abs(a), axis=1))max ⁡ ( ∣ a ∣ ) -infmin(sum(abs(a), axis=1)) min ⁡ ( ∣ a ∣ ) 0-##sum(a!= 0)max(sum(abs(a), axis=0))-1min(sum(abs(a), axis=0))2-2## If ord is a non-zero integer, recorded as n nn. Let a i a_iai be the elements in matrix a aa, then the n nn norm of the matrix is ​​

Frobenius norm	2-Norm
Frobenius norm	-
Nuclear norm		##inf
		1
		2-Norm (maximum singular value)
		Minimum singular value
		a is a vector, if

nuclear norm The number is also called the "trace norm" and represents the sum of all singular values ​​of the matrix. Frobenius norm can be defined as

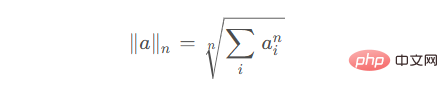
The essence is the natural generalization of the 2-norm of vectors in matrices.

In addition to

scipy.linalg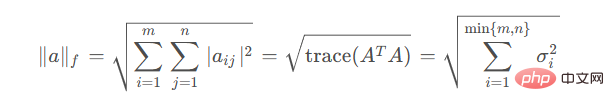

, norm

is also provided in

numpy.linalg

, and its parameters are

norm(x, ord=None, axis=None, keepdims=False)

The optional parameters of order are the same as the norm function in scipy.linalg

.

DeterminantIn scipy.linalg, the determinant function is det

, and its definition is very simple, except for the matrix to be found

Apart from a

, there are only override switches and limited checks of

a. The example is as follows

import numpy as np
from scipy import linalg
a = np.array([[1,2,3], [4,5,6], [7,8,9]])
linalg.det(a)
# 0.0
a = np.array([[0,2,3], [4,5,6], [7,8,9]])
linalg.det(a)
# 3.0

tracescipy.linalg

does not provide the

trace

function, but

numpy

Provided, it is defined as

umpy.trace(a, offset=0, axis1=0, axis2=1, dtype=None, out=None)

whereoffset

is the offset, indicating the offset relative to the main diagonal

• axis1, axis2 represents the coordinate axis

• ##dtype

  The data type used to adjust the output value

  >>> x = np.random.rand(3,3)
  >>> print(x)
  [[0.26832187 0.64615363 0.09006217]
   [0.63106319 0.65573765 0.35842304]
   [0.66629322 0.16999836 0.92357658]]
  >>> np.trace(x)
  1.8476361016546932

  The above is the detailed content of How to use Python to find the norm and determinant of a matrix. For more information, please follow other related articles on the PHP Chinese website!