How to implement Kruskal algorithm in Java

Introduction

There is another algorithm for constructing a minimum spanning tree, namely the Kruskal algorithm: Let the graph G=(V, E) be an undirected connected weighted graph, V={1,2,... n}; Suppose the minimum spanning tree T=(V, TE). The initial state of the tree has only n nodes and a non-connected graph with no edges T=(V, {}). Kruskal's algorithm treats these n nodes as n Isolated connected branches. It first sorts all the edges according to their weights from small to large, and then if the number of edges to be selected in T is less than n-1, it makes a greedy selection like this: select the edge (i,j) with the smallest weight in the edge set E ), if adding edge (i, j) to the set TE does not produce a cycle, then add edge (i, j) to the edge set TE, that is, use edge (i, j) to merge the two branches into a connected branch ; Otherwise, continue to select the next shortest edge. Delete the edge (i, j) from the set E and continue the greedy selection above until all nodes in T are on the same connected branch. At this time, the selected n-1 edges exactly constitute a minimum spanning tree T of the graph G.

Kruskal's algorithm uses a very smart method, which is to use sets to avoid circles; if the starting point and end point of the selected edge to join are both in the T set, it can be concluded that a loop will be formed, and the two changed nodes cannot Belong to the same collection.

Algorithm steps

1 Initialization. Sort all edges in ascending order of weight, and initialize each node set number to its own number.

2 Select the edge (u, v) with the smallest weight in the sorted order.

3 If nodes u and v belong to two different connected branches, add edge (u, v) to the edge set TE and merge the two connected branches.

4 If the number of selected edges is less than n-1, go to step 2, otherwise the algorithm ends.

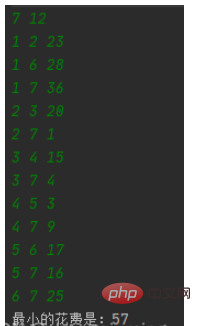
1. Picture after construction

2. Code

package graph.kruskal;
 
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;
 
public class Kruskal {
    static final int N = 100;
    static int fa[] = new int[N];
    static int n;
    static int m;
 
    static Edge e[] = new Edge[N * N];
    static List<Edge> edgeList = new ArrayList();
 
    static {
        for (int i = 0; i < e.length; i++) {
            e[i] = new Edge();
        }
    }
 
    // 初始化集合号为自身
    static void Init(int n) {
        for (int i = 1; i <= n; i++)
            fa[i] = i;
    }
 
    // 合并
    static int Merge(int a, int b) {
        int p = fa[a];
        int q = fa[b];
        if (p == q) return 0;
        for (int i = 1; i <= n; i++) { // 检查所有结点，把集合号是 q 的改为 p
            if (fa[i] == q)
                fa[i] = p; // a 的集合号赋值给 b 集合号
        }
        return 1;
    }
 
    // 求最小生成树
    static int Kruskal(int n) {
        int ans = 0;
        Collections.sort(edgeList);
        for (int i = 0; i < m; i++)
            if (Merge(edgeList.get(i).u, edgeList.get(i).v) == 1) {
                ans += edgeList.get(i).w;
                n--;
                if (n == 1)//n-1次合并算法结束
                    return ans;
            }
        return 0;
    }
 
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        m = scanner.nextInt();
        Init(n);
        for (int i = 1; i <= m; i++) {
            e[i].u = scanner.nextInt();
            e[i].v = scanner.nextInt();
            e[i].w = scanner.nextInt();
            edgeList.add(e[i]);
        }
        System.out.println("最小的花费是：" + Kruskal(n));
    }
}
 
class Edge implements Comparable {
    int u;
    int w;
    int v;
 
    @Override
    public int compareTo(Object o) {
        if (this.w > ((Edge) o).w) {
            return 1;
        } else if (this.w == ((Edge) o).w) {
            return 0;
        } else {
            return -1;
        }
    }
}

3. Test

Green is input, White is the output.

The above is the detailed content of How to implement Kruskal algorithm in Java. For more information, please follow other related articles on the PHP Chinese website!