 Technology peripherals
Technology peripherals
 AI
AI
 AI is once again involved in the world of mathematics, and new DSP methods double the success rate of machine proofs
AI is once again involved in the world of mathematics, and new DSP methods double the success rate of machine proofs
AI is once again involved in the world of mathematics, and new DSP methods double the success rate of machine proofs
Automatically proving mathematical theorems is an original intention of artificial intelligence and has always been a difficult problem. So far, human mathematicians have used two different ways of writing mathematics.
#The first is a method that everyone is familiar with, which is to use natural language to describe mathematical proofs. Most mathematics is written in this way, including mathematics textbooks, mathematics papers, etc.
#The second type is called formal mathematics. This is a tool created by computer scientists over the past half century to check mathematical proofs.
It seems today that computers can be used to verify mathematical proofs, but they can only do so using specially designed proof languages that cannot handle mathematical symbols. and a mixture of written texts used by mathematicians. Converting mathematical problems written in natural language into formal code so that computers can more easily solve them may help build machines that can explore new discoveries in mathematics. This process is called formalisation, and autoformalization refers to the task of automatically translating mathematics from natural language into a formal language.
Automation of formal proofs is a challenging task, and deep learning methods have not yet achieved great success in this field, mainly due to the scarcity of formal data. In fact, formal proof itself is very difficult and only a few experts can do it, which makes large-scale annotation efforts unrealistic. The largest corpus of formal proofs is written in Isabelle code (Paulson, 1994) and is less than 0.6GB in size, orders of magnitude smaller than commonly used datasets in vision or natural language processing. To address the scarcity of formal proofs, previous studies have proposed using synthetic data, self-supervised or reinforcement learning to synthesize additional formal training data. Although these methods alleviate the lack of data to a certain extent, they are unable to fully utilize the large number of manually written mathematical proofs.
Let’s take the language model Minerva as an example. After training with enough data, we found that its math ability is very strong and it can get higher than average scores in high school math tests. However, such a language model also has shortcomings. It can only imitate, but cannot train independently to improve mathematics. Formal proof systems provide a training environment, but there is very little data for formal mathematics.
Unlike formal mathematics, informal mathematical data is abundant and widely available. Recently, large language models trained on informal mathematical data have demonstrated impressive quantitative reasoning capabilities. However, they often produce faulty proofs, and automatically detecting faulty reasoning in these proofs is challenging.
In a recent work, researchers such as Yuhuai Tony Wu of Google designed a new method called DSP (Draft, Sketch, and Prove). Convert informal mathematical proofs into formal proofs, thus possessing both the logical rigor provided by formal systems and a large amount of informal data.

Paper link: https://arxiv.org/pdf/2210.12283.pdf
Earlier this year, Wu Yuhuai and several collaborators used the neural network of OpenAI Codex to perform automatic formalization work, demonstrating that a large language model can be used to automatically translate informal statements into Feasibility of formal statements. DSP goes a step further and uses large language models to generate formal proof sketches from informal proofs. Proof sketches consist of high-level reasoning steps that can be interpreted by a formal system like an interactive theorem prover. They differ from complete formal proofs in that they contain sequences of unjustified intermediate conjectures. In the final step of the DSP, the formal proof sketch is elaborated into a complete formal proof, using an automatic verifier to prove all intermediate conjectures.
Wu Yuhuai said: Now, we have shown that LLM can convert the informal proofs it generates into verified formal proofs!
Method
The Method section describes the DSP method for formal proof automation, which utilizes informal proofs to guide automatic formal theorem proving. Proof sketch of the device. It is assumed here that each problem has an informal proposition and a formal proposition describing the problem. The overall pipeline consists of three stages (shown in Figure 1).
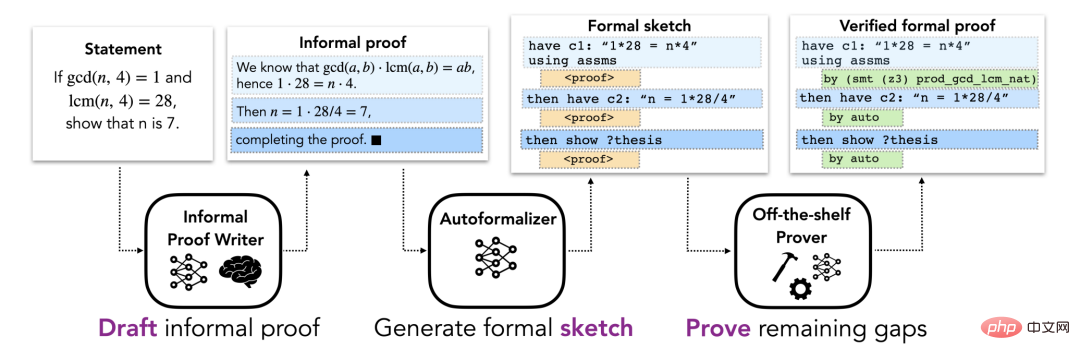
##Figure 1.
Informal proof The initial stage of drafting aDSP approach involves finding an informal proof for the problem based on its description in a natural mathematical language (possibly in LATEX). The resulting informal proof is treated as a rough draft for subsequent stages. In mathematics textbooks, proofs of theorems are generally provided, but sometimes they are missing or incomplete. Therefore, the researchers considered two situations corresponding to the presence or absence of informal proofs.
In the first case, the researcher assumes that there is a "real" informal proof (that is, a proof written by a human), which is the formal practice of existing mathematical theory typical situations. In the second case, the researchers make a more general assumption that no real informal proof is given, and use a large language model trained on informal mathematical data to draft proof candidates. The language model eliminates the dependence on human proofs and can generate multiple alternative solutions to each problem. While there is no easy way to automatically verify the correctness of these proofs, informal proofs only need to be useful at the next stage in generating a good formal proof sketch.
Mapping informal proofs into formal sketchesFormal proof sketches encode the structure of a solution and leave aside low-level details. Intuitively, it is a partial proof that outlines a high-level conjectural statement. Figure 2 is a concrete example of a proof sketch. Although informal proofs often leave aside low-level details, these details cannot be excluded in formal proofs, making the direct conversion of informal to formal proofs difficult. Instead, this paper proposes mapping informal proofs onto formal proof sketches that share the same high-level structure. Low-level details missing from the proof sketch can be filled in by the automatic prover. Since large informal-formal parallel corpora do not exist, standard machine translation methods are not suitable for this task. Instead, the few-shot learning capabilities of a large language model are used here. Specifically, some example pairs containing informal proofs and their corresponding formal sketches are used to prompt the model, followed by an informal proof to be converted, and then let the model generate subsequent tokens to obtain the required formal sketch. This model is called an "automatic formalizer".

##Figure 2.Proof of Disclosure in Sketch Guess
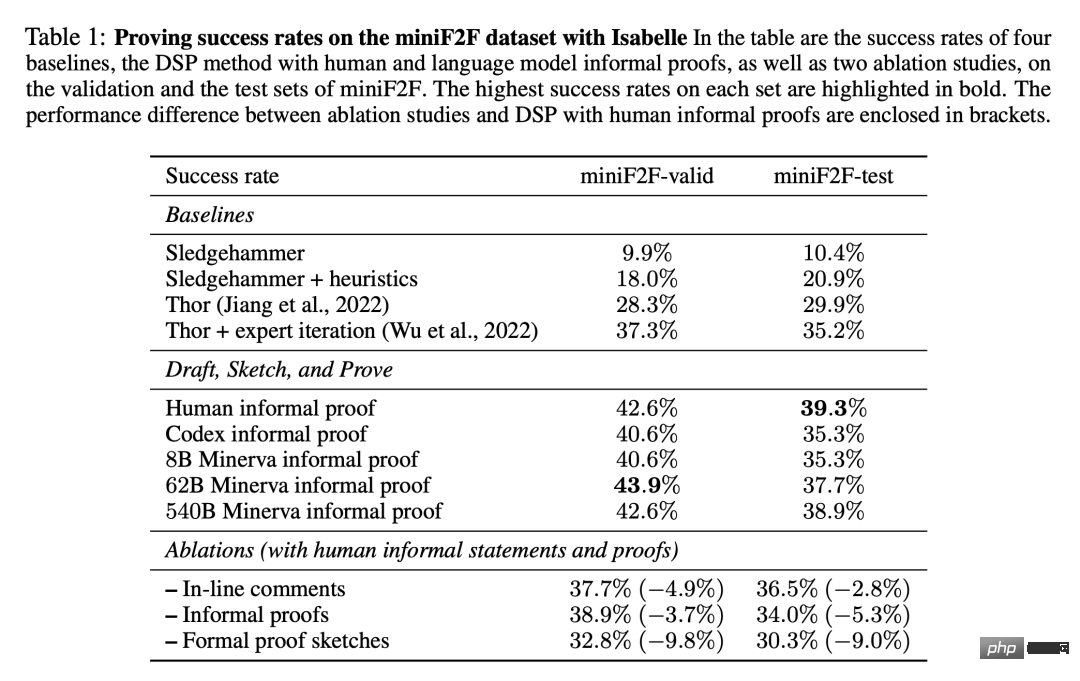
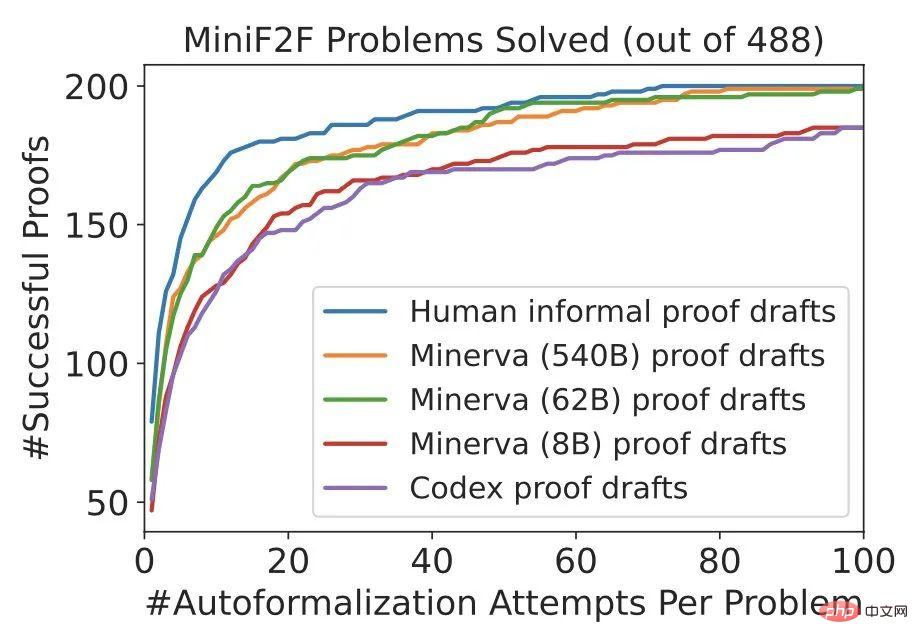
As the last part of this process, the researcher implements an off-the-shelf automatic prover to fill in the missing details in the proof sketch. The "automatic prover" here refers to one that can produce a formally verifiable proof. Proven system. The framework is agnostic to the specific choice of the automatic prover: it can be a symbolic prover (such as a heuristic proof automation tool), a neural network-based prover, or a hybrid approach. If the automatic prover successfully fills in all the gaps in the proof sketch, it returns a final formal proof that can be checked against the specification of the problem. If the automatic prover fails (for example, it exceeds the allocated time limit), the evaluation is considered unsuccessful.The researchers conducted a series of experiments, including formal proofs of problems generated from the miniF2F dataset, and showed that a large proportion of theorems can be automatically proved using this method. Two environments are studied here, where informal proofs are written by humans or drafted by a large language model trained on mathematical text. These two settings correspond to situations that often occur in the formalization of existing theories, that is, there are often informal proofs, but they are sometimes left as an exercise to the reader, or are missing due to constraints in the margins. Table 1 shows the proportion of successful formal proofs found on the miniF2F dataset. The results include four baselines from our experiments, as well as the DSP method with human-written proofs and model-generated proofs. It can be seen that the automatic prover with 11 heuristic strategies has greatly increased the performance of Sledgehammer. miniF2F improves its success rate from 9.9% to 18.0% on the validation set and from 10.4% to 20.9% on the test set. Two baselines using language models and proof search achieved success rates of 29.9% and 35.2% respectively on the test set of miniF2F. Based on human-written informal proofs, the DSP approach achieves success rates of 42.6% and 39.3% on the validation and test sets of miniF2F. A total of 200 of the 488 problems can be proved in this way. The Codex model and the Minerva (8B) model gave very similar results when solving problems on miniF2F: they both guided the automatic verifier to solve 40.6% and 35.3% of the problems on the validation and test sets respectively. When switching to the Minerva (62B) model, the success rates increased to 43.9% and 37.7% respectively. Compared to human-written informal proofs, its success rate is 1.3% higher on the validation set and 1.6% lower on the test set. Overall, the Minerva (62B) model is able to solve 199 problems on miniF2F, one less than a human-written proof. The Minerva (540B) model solved 42.6% and 38.9% of the problems in miniF2F's validation set and test set, respectively, and also generated 199 successful proofs. The DSP approach effectively guides automated provers in both cases: informal proofs using humans or informal proofs generated by language models. DSP nearly doubles the prover success rate and produces SOTA performance on miniF2F using Isabelle. Furthermore, larger Minerva models are almost as helpful as humans in guiding automated formal provers. As shown in the figure below, the DSP method significantly improves the performance of the Sledgehammer heuristic prover (~20% -> ~40%), achieving a new SOTA on miniF2F. The 62B and 540B versions of Minerva generate proofs that are very similar to human proofs. For more information, please refer to the original paper. Experiments
The above is the detailed content of AI is once again involved in the world of mathematics, and new DSP methods double the success rate of machine proofs. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
 How to solve the complexity of WordPress installation and update using Composer
Apr 17, 2025 pm 10:54 PM
How to solve the complexity of WordPress installation and update using Composer
Apr 17, 2025 pm 10:54 PM
When managing WordPress websites, you often encounter complex operations such as installation, update, and multi-site conversion. These operations are not only time-consuming, but also prone to errors, causing the website to be paralyzed. Combining the WP-CLI core command with Composer can greatly simplify these tasks, improve efficiency and reliability. This article will introduce how to use Composer to solve these problems and improve the convenience of WordPress management.
 How to solve SQL parsing problem? Use greenlion/php-sql-parser!
Apr 17, 2025 pm 09:15 PM
How to solve SQL parsing problem? Use greenlion/php-sql-parser!
Apr 17, 2025 pm 09:15 PM
When developing a project that requires parsing SQL statements, I encountered a tricky problem: how to efficiently parse MySQL's SQL statements and extract the key information. After trying many methods, I found that the greenlion/php-sql-parser library can perfectly solve my needs.
 How to solve complex BelongsToThrough relationship problem in Laravel? Use Composer!
Apr 17, 2025 pm 09:54 PM
How to solve complex BelongsToThrough relationship problem in Laravel? Use Composer!
Apr 17, 2025 pm 09:54 PM
In Laravel development, dealing with complex model relationships has always been a challenge, especially when it comes to multi-level BelongsToThrough relationships. Recently, I encountered this problem in a project dealing with a multi-level model relationship, where traditional HasManyThrough relationships fail to meet the needs, resulting in data queries becoming complex and inefficient. After some exploration, I found the library staudenmeir/belongs-to-through, which easily installed and solved my troubles through Composer.
 Solve CSS prefix problem using Composer: Practice of padaliyajay/php-autoprefixer library
Apr 17, 2025 pm 11:27 PM
Solve CSS prefix problem using Composer: Practice of padaliyajay/php-autoprefixer library
Apr 17, 2025 pm 11:27 PM
I'm having a tricky problem when developing a front-end project: I need to manually add a browser prefix to the CSS properties to ensure compatibility. This is not only time consuming, but also error-prone. After some exploration, I discovered the padaliyajay/php-autoprefixer library, which easily solved my troubles with Composer.
 How to solve the problem of PHP project code coverage reporting? Using php-coveralls is OK!
Apr 17, 2025 pm 08:03 PM
How to solve the problem of PHP project code coverage reporting? Using php-coveralls is OK!
Apr 17, 2025 pm 08:03 PM
When developing PHP projects, ensuring code coverage is an important part of ensuring code quality. However, when I was using TravisCI for continuous integration, I encountered a problem: the test coverage report was not uploaded to the Coveralls platform, resulting in the inability to monitor and improve code coverage. After some exploration, I found the tool php-coveralls, which not only solved my problem, but also greatly simplified the configuration process.
 How to solve the complex problem of PHP geodata processing? Use Composer and GeoPHP!
Apr 17, 2025 pm 08:30 PM
How to solve the complex problem of PHP geodata processing? Use Composer and GeoPHP!
Apr 17, 2025 pm 08:30 PM
When developing a Geographic Information System (GIS), I encountered a difficult problem: how to efficiently handle various geographic data formats such as WKT, WKB, GeoJSON, etc. in PHP. I've tried multiple methods, but none of them can effectively solve the conversion and operational issues between these formats. Finally, I found the GeoPHP library, which easily integrates through Composer, and it completely solved my troubles.
 git software installation tutorial
Apr 17, 2025 pm 12:06 PM
git software installation tutorial
Apr 17, 2025 pm 12:06 PM
Git Software Installation Guide: Visit the official Git website to download the installer for Windows, MacOS, or Linux. Run the installer and follow the prompts. Configure Git: Set username, email, and select a text editor. For Windows users, configure the Git Bash environment.
 The latest tutorial on how to read the key of git software
Apr 17, 2025 pm 12:12 PM
The latest tutorial on how to read the key of git software
Apr 17, 2025 pm 12:12 PM
This article will explain in detail how to view keys in Git software. It is crucial to master this because Git keys are secure credentials for authentication and secure transfer of code. The article will guide readers step by step how to display and manage their Git keys, including SSH and GPG keys, using different commands and options. By following the steps in this guide, users can easily ensure their Git repository is secure and collaboratively smoothly with others.



