How to use adjacency list to store graph in Java

1. The finishing touch

The adjacency list is a chain storage method for graphs. Its data structure consists of two parts: nodes and adjacency points.

Adjacency lists can be used to represent undirected graphs, directed graphs and networks. This is explained using an undirected graph.

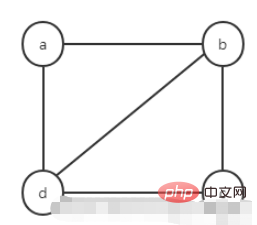
1. Undirected graph

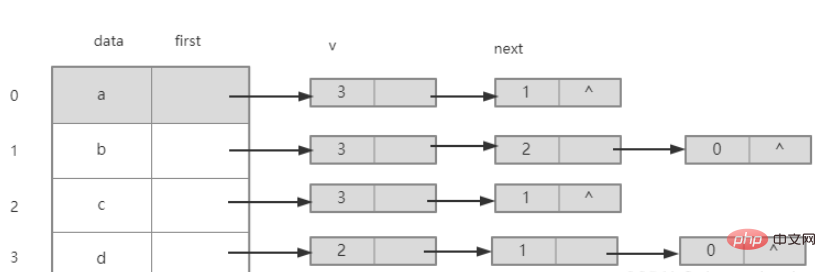
2. Linked table of undirected graph

3 .Explanation

The adjacent points of node a are nodes b and d, and the storage subscripts of their adjacent points are 1 and 3. Put them into the singly linked list behind node a according to the head interpolation method (reverse order).

The adjacent points of node b are nodes a, c, and d. The storage subscripts of their adjacent points are 0, 2, and 3. Put them into the singly linked list behind node b according to the head interpolation method (reverse order). middle.

The adjacent points of node c are nodes b and d, and the storage subscripts of their adjacent points are 1 and 3. They are put into the singly linked list behind node c according to the head insertion method (reverse order).

The adjacent points of node d are nodes a, b, and c. The storage subscripts of their adjacent points are 0, 1, and 2. They are put into the singly linked list behind node d according to the head interpolation method (reverse order). middle.

4. Undirected graph

The characteristics of the adjacency list are as follows. If there are n nodes and e edges in the undirected graph, then there are n nodes in the node table and 2e in the neighbor node table. nodes.

The degree of a node is the number of nodes in the singly linked list behind the node.

2. Data structure of adjacency list

1. Node

includes node information data and a pointer to the first adjacent point first.

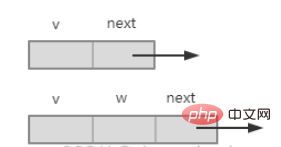
2. Adjacency point

Includes the storage subscript v of the adjacent point and the pointer to the next adjacent point next, if it is an adjacent point of the network , then a weight domain w needs to be added, as shown in the figure below.

3. Algorithm steps

1 Enter the number of nodes and edges.

2 Enter the node information in turn, store it in the data field of the node array Vex[], and leave the Vex[] first field blank.

3 Enter the two nodes attached to each edge in turn. If it is a network, you also need to enter the weight of the edge.

If it is an undirected graph, enter a b, query nodes a, b, store the subscripts i, j in the node array Vex[], create a new adjacent point s, let s.v = j;s .next=null;Then insert node s before the first adjacent point of the i-th node (head interpolation method). In an undirected graph, there is an edge from node a to node b, and there is an edge from node b to node a, so a new adjacency point s2 needs to be created, let s2.v = i;s2.next=null; and then let The s2 node is inserted before the first adjacent point of the j-th node (head interpolation method).

If it is an undirected graph, enter a b, query nodes a, b, store the subscripts i, j in the node array Vex[], create a new adjacent point s, let s.v = j;s .next=null;Then insert node s before the first adjacent point of the i-th node (head interpolation method).

If it is an undirected network or a directed network, it is processed in the same way as an undirected graph or a directed graph, except that the neighboring nodes have an additional weight domain.

4. Implementation

package graph;
 
import java.util.Scanner;
 
public class CreateALGraph {
    static final int MaxVnum = 100;  // 顶点数最大值
 
    public static void main(String[] args) {
        ALGraph G = new ALGraph();
        for (int i = 0; i < G.Vex.length; i++) {
            G.Vex[i] = new VexNode();
        }
        CreateALGraph(G); // 创建有向图邻接表
        printg(G); // 输出邻接表
    }
 
    static int locatevex(ALGraph G, char x) {
        for (int i = 0; i < G.vexnum; i++) // 查找顶点信息的下标
            if (x == G.Vex[i].data)
                return i;
        return -1; // 没找到
    }
 
    // 插入一条边
    static void insertedge(ALGraph G, int i, int j) {
        AdjNode s = new AdjNode();
        s.v = j;
        s.next = G.Vex[i].first;
        G.Vex[i].first = s;
    }
 
    // 输出邻接表
    static void printg(ALGraph G) {
        System.out.println("----------邻接表如下：----------");
 
        for (int i = 0; i < G.vexnum; i++) {
            AdjNode t = G.Vex[i].first;
            System.out.print(G.Vex[i].data + "：  ");
            while (t != null) {
                System.out.print("[" + t.v + "]\t");
                t = t.next;
            }
            System.out.println();
        }
    }
 
    // 创建有向图邻接表
    static void CreateALGraph(ALGraph G) {
        int i, j;
        char u, v;
 
        System.out.println("请输入顶点数和边数:");
        Scanner scanner = new Scanner(System.in);
        G.vexnum = scanner.nextInt();
        G.edgenum = scanner.nextInt();
        System.out.println("请输入顶点信息:");
 
        for (i = 0; i < G.vexnum; i++)//输入顶点信息，存入顶点信息数组
            G.Vex[i].data = scanner.next().charAt(0);
        for (i = 0; i < G.vexnum; i++)
            G.Vex[i].first = null;
        System.out.println("请依次输入每条边的两个顶点u,v");
 
        while (G.edgenum-- > 0) {
            u = scanner.next().charAt(0);
            v = scanner.next().charAt(0);
            i = locatevex(G, u); // 查找顶点 u 的存储下标
            j = locatevex(G, v); // 查找顶点 v 的存储下标
            if (i != -1 && j != -1)
                insertedge(G, i, j);
            else {
                System.out.println("输入顶点信息错！请重新输入！");
                G.edgenum++; // 本次输入不算
            }
        }
    }
}
 
// 定义邻接点类型
class AdjNode {
    int v; // 邻接点下标
    AdjNode next; // 指向下一个邻接点
}
 
// 定义顶点类型
class VexNode {
    char data; // VexType为顶点的数据类型，根据需要定义
    AdjNode first; // 指向第一个邻接点
}
 
// 定义邻接表类型
class ALGraph {
    VexNode Vex[] = new VexNode[CreateALGraph.MaxVnum];
    int vexnum; // 顶点数
    int edgenum; // 边数
}

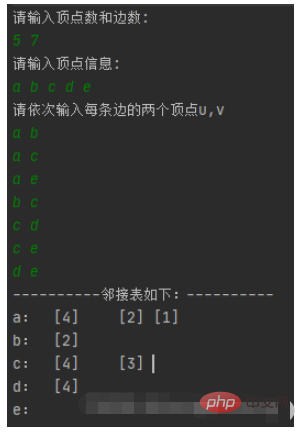
5. Test

White is output, green is input

The above is the detailed content of How to use adjacency list to store graph in Java. For more information, please follow other related articles on the PHP Chinese website!