How to analyze the Tower of Hanoi problem using Java
1. Source of the Tower of Hanoi problem
The Tower of Hanoi, also known as the Tower of Hanoi, is an educational toy originating from ancient Indian legends. When Brahma created the world, he made three diamond pillars. On one pillar, 64 gold discs were stacked in order of size from bottom to top. Brahma ordered the Brahmin to rearrange the disks on another pillar in order of size from the bottom. And it is stipulated that the disk cannot be enlarged on the small disk, and only one disk can be moved between the three pillars at a time

 ## 1. A -> C
## 1. A -> C
##2. A -> B
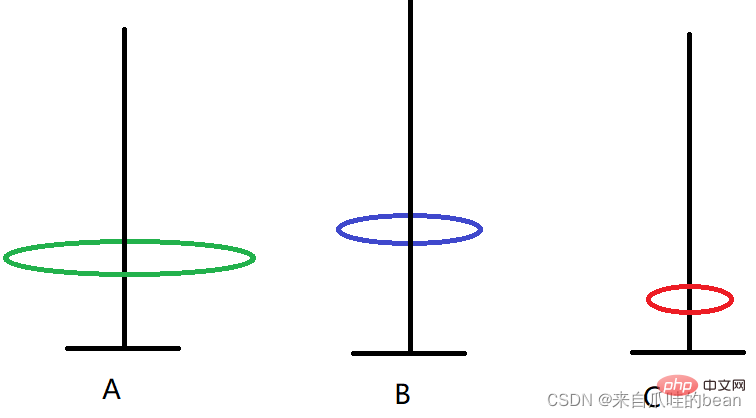
##4. A -> C
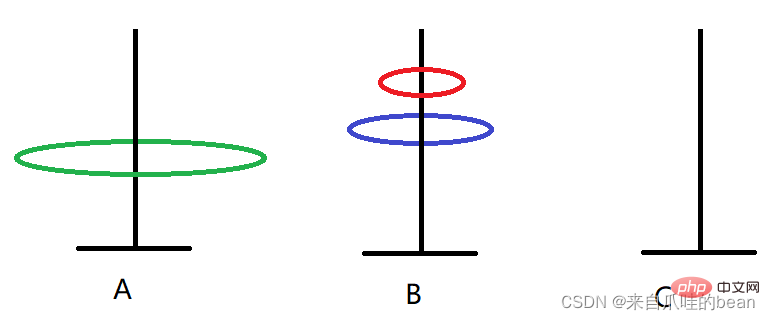
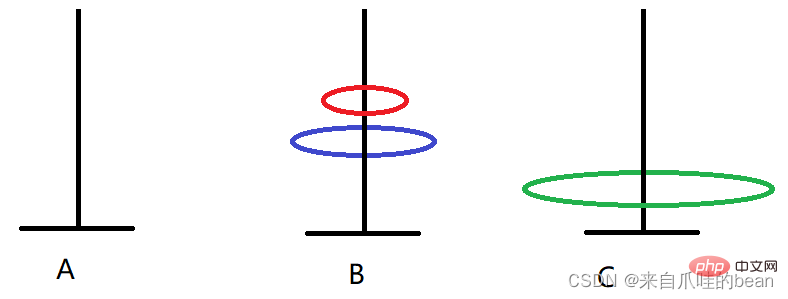
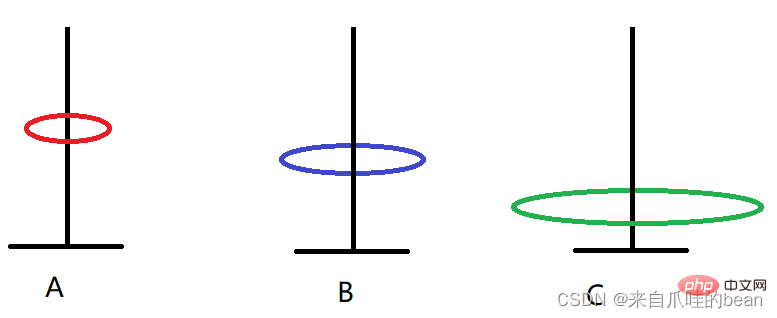
 Rule derivation
Rule derivation
1 plate Move 1 time
2 plates Move 3 times
3 plates Move 7 times
......
N plates move 2^N - 1 time
Then 64 plates need to be moved 2^64 - 1 time
3. Solve the problem
We can solve this problem through recursion and obtain the correct way of moving
How to move if there are N plates?
Overall idea
We can first move N - 1 plates from column A to column B with the help of column C, then move the remaining plate from column A to column C, and then move N - 1 plates on pillar B are moved to pillar C with the help of pillar A, thus completing the movement of all pillars (the specific moving process in the middle will not be discussed for now)
上码
public static void hanoi(int num, String src, String help, String dest) {
if (num == 1) { // 只有一个盘子的时候直接移动
System.out.print(src + "->" + dest + " "); // 将一个盘子从源柱子挪到目标柱子
} else {
hanoi(num - 1, src, dest, help); // 将n - 1个盘子从源柱子借助目标柱子挪到辅助柱子
System.out.print(src + "->" + dest + " "); // 将一个盘子从源柱子挪到目标柱子
hanoi(num - 1, help, src, dest); // 将辅助柱子上n - 1个盘子借助源柱子挪到目标柱子
}
}
public static void main(String[] args) {
hanoi(3, "A", "B", "C");
}this paragraph In the code, src is the source pillar, help is the auxiliary pillar, and dest is the target pillar.
This is a two-way recursion.
Running results:
This successfully completed the movement of the plates4. Can Brahman complete the task of Brahma? How long does it take to move 64 plates
How long does it take to move 64 plates
Here we assume Brahmins are very smart and can directly know the correct way to move without thinking. It takes one second to move a plate, and they keep moving
Converting 2^64 - 1 second into years is about 5849 4241 7355 years (584.942 billion years). The earth has only existed for 4.5 billion years, and the expected lifespan of the solar system is said to be tens of billions of years. It has really been 584.942 billion years. Not to mention the solar system and the Milky Way, at least all life on the earth, including the Vatican Towers, temples, etc., have long been wiped out.
Related prophecies
There is a prophecy that when this thing is completed, the universe will be destroyed in a flash. Some people also believe that Brahmins are still moving the disks all the time.
How long does it take for a computer to move 64 plates?
The core frequency of my computer is 2.90GHz, which is 2.9 billion operations per second, so the time required to move 2^64 - 1 time is about 201 years
The above is the detailed content of How to analyze the Tower of Hanoi problem using Java. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1387
1387
 52
52
 Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Perfect Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Perfect Number in Java. Here we discuss the Definition, How to check Perfect number in Java?, examples with code implementation.
 Weka in Java
Aug 30, 2024 pm 04:28 PM
Weka in Java
Aug 30, 2024 pm 04:28 PM
Guide to Weka in Java. Here we discuss the Introduction, how to use weka java, the type of platform, and advantages with examples.
 Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Smith Number in Java
Aug 30, 2024 pm 04:28 PM
Guide to Smith Number in Java. Here we discuss the Definition, How to check smith number in Java? example with code implementation.
 Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
Java Spring Interview Questions
Aug 30, 2024 pm 04:29 PM
In this article, we have kept the most asked Java Spring Interview Questions with their detailed answers. So that you can crack the interview.
 Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Break or return from Java 8 stream forEach?
Feb 07, 2025 pm 12:09 PM
Java 8 introduces the Stream API, providing a powerful and expressive way to process data collections. However, a common question when using Stream is: How to break or return from a forEach operation? Traditional loops allow for early interruption or return, but Stream's forEach method does not directly support this method. This article will explain the reasons and explore alternative methods for implementing premature termination in Stream processing systems. Further reading: Java Stream API improvements Understand Stream forEach The forEach method is a terminal operation that performs one operation on each element in the Stream. Its design intention is
 TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
TimeStamp to Date in Java
Aug 30, 2024 pm 04:28 PM
Guide to TimeStamp to Date in Java. Here we also discuss the introduction and how to convert timestamp to date in java along with examples.
 Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Java Program to Find the Volume of Capsule
Feb 07, 2025 am 11:37 AM
Capsules are three-dimensional geometric figures, composed of a cylinder and a hemisphere at both ends. The volume of the capsule can be calculated by adding the volume of the cylinder and the volume of the hemisphere at both ends. This tutorial will discuss how to calculate the volume of a given capsule in Java using different methods. Capsule volume formula The formula for capsule volume is as follows: Capsule volume = Cylindrical volume Volume Two hemisphere volume in, r: The radius of the hemisphere. h: The height of the cylinder (excluding the hemisphere). Example 1 enter Radius = 5 units Height = 10 units Output Volume = 1570.8 cubic units explain Calculate volume using formula: Volume = π × r2 × h (4
 Create the Future: Java Programming for Absolute Beginners
Oct 13, 2024 pm 01:32 PM
Create the Future: Java Programming for Absolute Beginners
Oct 13, 2024 pm 01:32 PM
Java is a popular programming language that can be learned by both beginners and experienced developers. This tutorial starts with basic concepts and progresses through advanced topics. After installing the Java Development Kit, you can practice programming by creating a simple "Hello, World!" program. After you understand the code, use the command prompt to compile and run the program, and "Hello, World!" will be output on the console. Learning Java starts your programming journey, and as your mastery deepens, you can create more complex applications.




