A quantum problem that required 100,000 equations to be solved was compressed by AI into just four without sacrificing accuracy.

Interacting electrons exhibit a variety of unique phenomena at different energies and temperatures. If we change their surrounding environment, they will exhibit new collective behaviors, such as spin, pairing fluctuations, etc. However, There are still many difficulties in dealing with these phenomena between electrons. Many researchers use Renormalization Group (RG) to solve this problem.

In the context of high-dimensional data, the emergence of machine learning (ML) technology and data-driven methods has aroused great interest among researchers in quantum physics. So far, ML ideas have used in the interaction of electronic systems.

In this article, physicists from the University of Bologna and other institutions use artificial intelligence to compress a quantum problem that has so far required 100,000 equations into one with only 4 equations. small tasks, all without sacrificing accuracy, the research was published today in Physical Review Letters.

##Paper address: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.136402

Domenico Di Sante, the first author of the study and assistant professor at the University of Bologna, said: We coupled this huge project together and then used machine learning to condense it into something that can be counted on one finger. task.

This study dealt with the question of how electrons behave as they move across a grid-like lattice. According to existing experience, when two electrons occupy the same lattice lattice, they will interact. This phenomenon, known as the Hubbard model, is an idealized setup of some materials that allows scientists to understand how electrons behave to create phases of matter, such as superconductivity, where electrons flow through the material without resistance. The model can also serve as a testing ground for new methods before they are applied to more complex quantum systems.

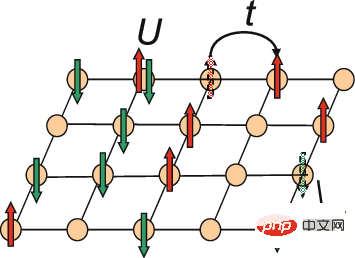
Schematic diagram of the two-dimensional Hubbard model

The Hubbard model seems simple. But even using cutting-edge computing methods to process small numbers of electrons requires a lot of computing power. This is because when electrons interact, they become quantum mechanically entangled: even if the electrons are located far apart in the lattice, the two electrons cannot be dealt with independently, so physicists must deal with them all simultaneously. electrons, rather than working with one electron at a time. The more electrons there are, the more quantum mechanical entanglement there will be, and the computational difficulty will increase exponentially.

A common method to study quantum systems is the renormalization group. As a mathematical device, physicists use it to observe the behavior of a system, such as the Hubbard model. Unfortunately, a renormalization group records all possible couplings between electrons, which may contain thousands, hundreds of thousands, or even millions of independent equations that need to be solved. On top of that, the equations are complex: each equation represents a pair of interacting electrons.

The Di Sante team wondered if they could use a machine learning tool called a neural network to make renormalization groups more manageable.

In the case of neural networks, first, researchers use machine learning procedures to establish connections to full-size renormalization groups; then the neural network adjusts the strength of these connections until it finds a small A set of equations that yields the same solution as the original, very large renormalization group. We end up with four equations, and even though there are only four, the program's output captures the physics of Hubbard's model.

Di Sante said: "A neural network is essentially a machine that can discover hidden patterns, and this result exceeded our expectations."

Training machine learning programs requires a lot of computing power, so they took weeks to complete. The good news is that now that their program is up and running, a few tweaks can solve other problems without having to start from scratch.

When talking about future research directions, Di Sante said it is necessary to verify how effective the new method is on more complex quantum systems. In addition, Di Sante says there are great possibilities for using the technique in other fields regarding renormalization groups, such as cosmology and neuroscience.

Paper Overview

We describe the scale-dependent four-dimensional functional renormalization group (fRG) flow characteristics of the widely studied two-dimensional t-t' Hubbard model on square crystals. Vertex function, the researchers performed data-driven dimensionality reduction. They demonstrate that a deep learning architecture based on a neural regular differential equation (NODE) ​​solver in a low-dimensional latent space can efficiently learn the fRG dynamics describing various magnetic and d-wave superconducting states of the Hubbard model.

The researchers further proposed dynamic mode decomposition analysis, which can confirm that a few modes are indeed sufficient to capture fRG dynamics. The research demonstrates the possibility of using artificial intelligence to extract compact representations of relevant electron four-vertex functions, which is the most important goal to successfully implement cutting-edge quantum field theory methods and solve many-electron problems.

The basic object in fRG is the vertex function V(k_1, k_2, k_3), which in principle requires the calculation and storage of a function consisting of three continuous momentum variables. By studying specific theoretical patterns, the two-dimensional Hubbard model is thought to be relevant to cuprates and a wide range of organic conductors. We show that lower dimensional representations can capture the fRG flow of high-dimensional vertex functions.

The fRG ground state of the Hubbard model. The microscopic Hamiltonian considered by the researcher is shown in the following formula (1).

The 2-particle properties of the Hubbard model are studied through a one-loop fRG scheme of temperature flow, where The RG flow of 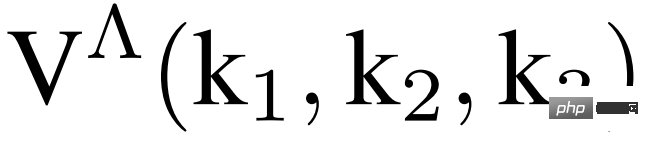is shown in the following formula (2).

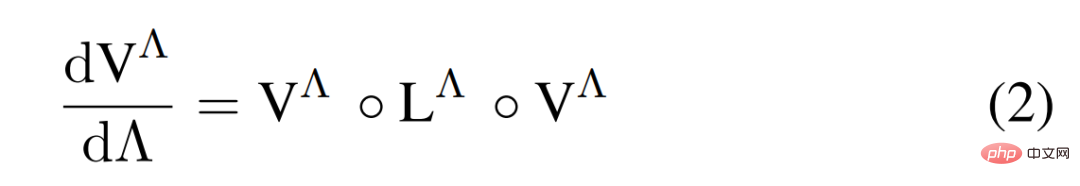
The following figure 1 a) is a graphical representation of the one-ring fRG flow equation of the 2-particle vertex function V^Λ.

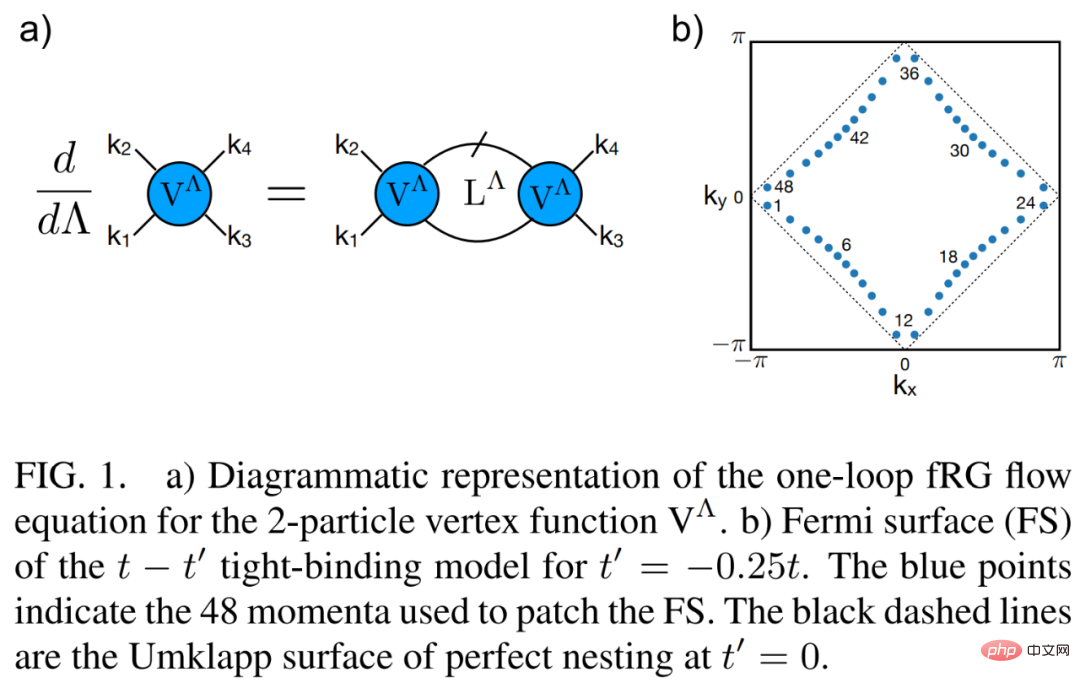
Next let’s look at deep learning fRG. As shown in Figure 2 b) below, by examining the 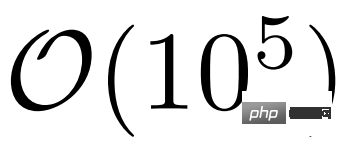coupling of the 2-particle vertex functions before the fRG flow tends to strong coupling and the one-ring approximate decomposition, the researchers realized that many of them either remain in the marginal state Either become irrelevant under RG flow.

The researcher implements a flexible dimensionality reduction scheme based on the parameterized NODE architecture suitable for current high-dimensional problems. This method is shown in Figure 2 a) below, focusing on deep neural networks.

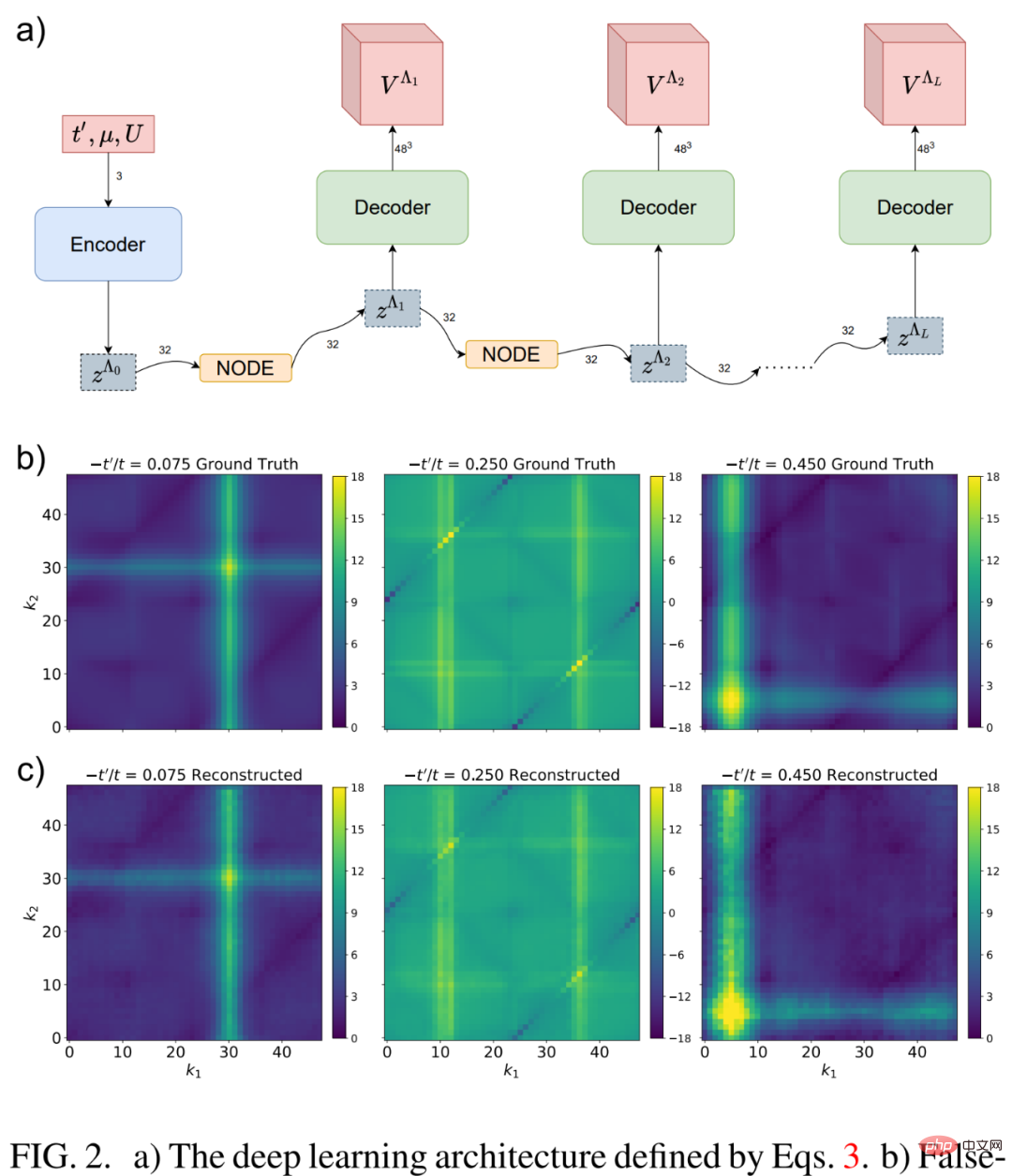
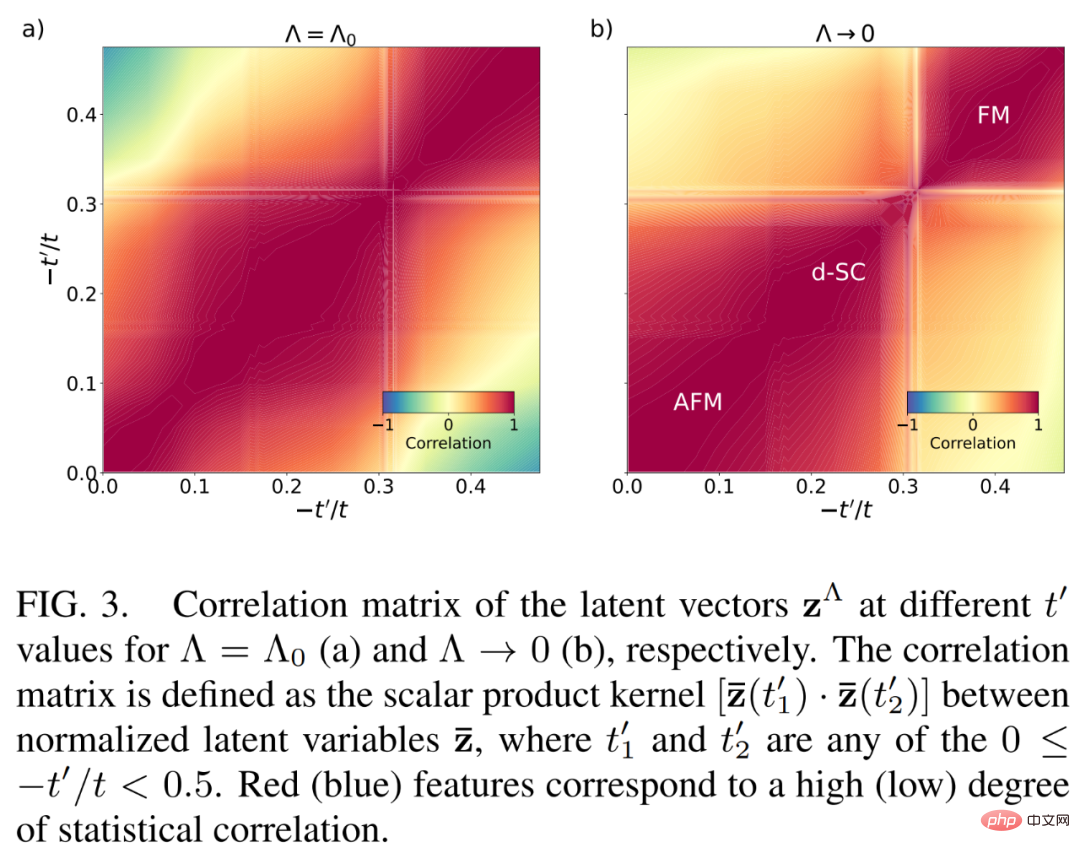
Figure 3 below shows three statistically highly correlated latent space representations z as NODE neural during the fRG dynamics of the latent space Learning characteristics of the Internet.

Please refer to the original paper for more details.

The above is the detailed content of A quantum problem that required 100,000 equations to be solved was compressed by AI into just four without sacrificing accuracy.. For more information, please follow other related articles on the PHP Chinese website!