Can machine learning really produce intelligent decisions?
After three years, we completed in 2022 Judy, winner of the Turing Award, professor of computer science at the University of California, Los Angeles, academician of the National Academy of Sciences, and known as the "Father of Bayesian Networks" A. Perl's masterpiece "Causation: Models, Reasoning, and Inference".
The original first edition of this book was written in 2000. It pioneered new ideas and methods of causal analysis and inference. It received widespread praise as soon as it was published and promoted data science. , artificial intelligence, machine learning, causal analysis and other fields have had a great impact on the academic community.
The second edition was later revised in 2009. The content was significantly changed based on the new developments in causal research at that time. The original English version of the book we are currently translating was published in 2009, so it has been more than ten years ago.
The publication of the Chinese version of this book will help Chinese scholars, students and practitioners in various fields understand and master the content related to causal models, reasoning and inference. Especially in the current era when statistics and machine learning are popular, how to achieve the transformation from "data fitting" to "data understanding"? How to move from the currently dominant assumption that “all knowledge comes from the data itself” to a completely new machine learning paradigm in the next decade? Will it trigger a "second artificial intelligence revolution"?
Just as the Turing Award was awarded to Pearl, his work was evaluated as "a fundamental contribution to the field of artificial intelligence. He proposed probabilistic and causal reasoning algorithms, which completely changed the initial development of artificial intelligence." A direction based on rules and logic." We expect this paradigm to bring new technical directions and forward momentum to machine learning, and ultimately be able to play a role in practical applications.
正 As Pearl said, "Data fitting currently firmly dominates the current fields of statistics and machine learning and is the main focus of most machine learning researchers today. research paradigm, especially those engaged in connectionism, deep learning and neural network technology." This paradigm with "data fitting" as its core has achieved great success in application fields such as computer vision, speech recognition and autonomous driving. An eye-catching success. However, many researchers in the field of data science have also realized that, from current practice, machine learning cannot produce the kind of understanding required for intelligent decision-making. These issues include: robustness, transferability, interpretability, etc. Let's look at an example below.
1. Are the statistics reliable?
In recent years, many people in the self-media think that they are statisticians. Because "data fitting" and "all knowledge comes from the data itself" provide statistical basis for many major decisions. However, we need to be cautious when doing this analysis. After all, things may not always be what they seem at first glance! A case closely related to our lives. Ten years ago, the house price in the city center was 8,000 yuan/square meter, with a total of 10 million square meters sold; in the high-tech zone, it was 4,000 yuan/square meter, with a total of 1 million square meters sold; overall, the city’s average house price was 7,636 yuan/square meter . Now, the price in the city center is 10,000 yuan/square meter, but because the land supply in the city center is less, only 2 million square meters have been sold; the high-tech zone is 6,000 yuan/square meter, but because there is more newly developed land, 20 million square meters have been sold; overall Look, the average house price in the city is now 6,363 yuan/square meter. Therefore, looking at the different areas, house prices have risen individually, but looking at it as a whole, there will be doubts: Why have house prices fallen now?
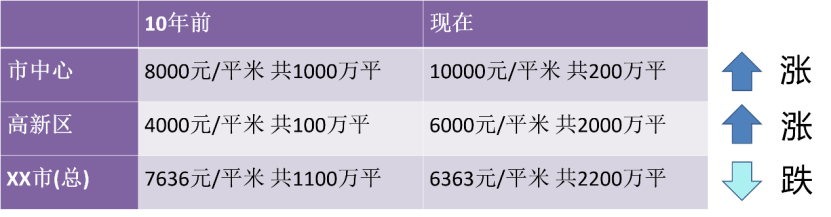
Figure 1 The housing price trend divided by different regions is contrary to the overall conclusion
We know this The phenomenon is called Simpson's Paradox. These cases clearly show how we can get completely wrong models and conclusions from statistical data when we are not given enough observed variables. In the case of this pandemic, we typically get nationwide statistics. If we grouped by region or city or county, we might come to very different conclusions. Across the country, we can observe a decline in the number of COVID-19 cases, although some areas are experiencing an increase in cases (which may signal the beginning of the next wave). This may also occur if there are widely different groups, such as areas with widely different populations. In national data, surges in cases in less densely populated areas may be dwarfed by declines in more densely populated areas.
Similar statistical problems based on "data fitting" abound. Take the following two interesting examples.
If we collect data on the number of movies played by Nicolas Cage and the number of drownings in the United States every year, we will find that these two variables are highly correlated, and the data fit is extremely high.
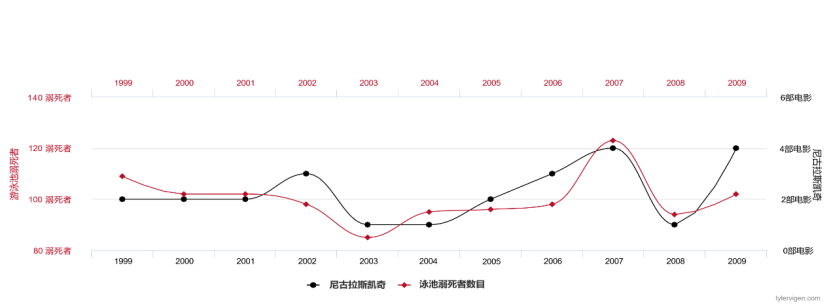
Figure 2 The number of movies played by Nicolas Cage and the number of people who drown in the United States each year
If we collect data on per capita milk sales and the number of Nobel Prize winners in each country, we will find that these two variables are highly correlated.
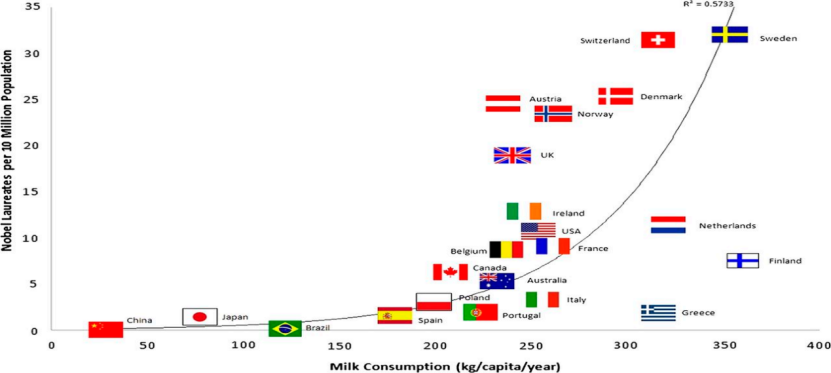
Figure 3 Per capita milk consumption and the number of Nobel Prizes
From our common sense as humans Intellectually speaking, these are spurious correlations, even paradoxes. But from the perspective of mathematics and probability theory, cases that exhibit spurious correlations or paradoxes are not problematic both from a statistical and computational perspective. Anyone with some causal basis knows that this happens because there are so-called lurking variables, unobserved confounders, hidden in the data.
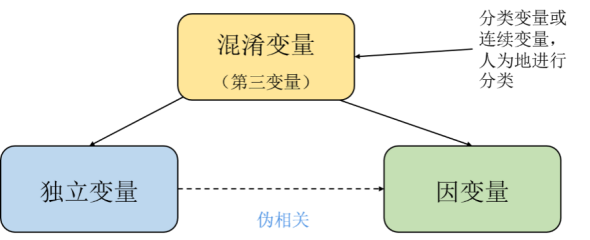
Figure 4 Independent variables lead to spurious correlation between two variables
Perl gave a solution paradigm in "The Theory of Causation", analyzed and derived the above problems in detail, and emphasized the essential difference between causation and statistics, although causal analysis and inference are still based on statistics. In the context of learning. Pearl proposed the basic calculation model of intervention operations (operators), including the backdoor principle and specific calculation formulas. This is currently the most mathematical description of causality. "Causation and related concepts (such as randomization, confounding, intervention, etc.) are not statistical concepts." This is a basic principle that runs through Pearl's causal analysis thinking, which Pearl calls the first principle [2].
So, with the current data-driven machine learning methods, especially those algorithms that rely heavily on statistical methods, the learned models are very likely to be half-true or half-false. Misleading or counterproductive results. This is because these models tend to learn based on the distribution of observed data, rather than the mechanism by which the data is generated.
2. Three issues that need to be solved urgently in machine learning
Robustness:With the popularity of deep learning methods, computers Research in vision, natural language processing, and speech recognition makes extensive use of state-of-the-art deep neural network structures. But there is still a long-term problem of the fact that in the real world, the distribution of the data we collect is usually rarely complete and may be inconsistent with the distribution in the real world. In computer vision applications, the distribution of training set and test set data may be affected by factors such as pixel difference, compression quality, or camera displacement, rotation, or angle. These variables are actually "intervention" issues in the concept of cause and effect. From this, simple algorithms have been proposed to simulate interventions to specifically test the generalization capabilities of classification and recognition models, such as spatial offsets, blurring, changes in brightness or contrast, background control and rotation, and acquisition in multiple environments. images etc. So far, although we have made some progress in robustness using methods such as data augmentation, pre-training, and self-supervised learning, there is no clear consensus on how to solve these problems. It has been argued that these corrections may not be sufficient, and that generalizing beyond the independent and identically distributed assumption requires learning not only statistical associations between variables but also underlying causal models that clarify the mechanisms by which the data were generated and allow simulation through intervening concepts Distribution changes.
Transferability: Infants’ understanding of objects is based on tracking objects that behave consistently over time. Such an approach allows infants to quickly learn new tasks because of their knowledge of the objects and Intuitive understanding can be reused. Similarly, being able to efficiently solve real-world tasks requires reusing learned knowledge and skills in new scenarios. Research has proven that machine learning systems that learn environmental knowledge are more efficient and more versatile. If we model the real world, many modules exhibit similar behavior in different tasks and environments. Therefore, when faced with a new environment or task, humans or machines may only need to adjust a few modules in their internal representation. When learning causal models, since most of the knowledge (i.e., modules) can be reused without further training, fewer samples are required to adapt to new environments or tasks.
Interpretability: Interpretability is a subtle concept that cannot be fully described using just the language of Boolean logic or statistical probability, it requires additional intervening concepts , or even the concept of counterfactuals. The definition of manipulability in causation focuses on the fact that conditional probabilities ("Seeing people open their umbrellas indicates it's raining") cannot reliably predict the outcomes of active interventions ("Putting your umbrellas away does not prevent it from raining" ). Causality is viewed as an integral part of a chain of inference that can provide predictions for situations that are far removed from the observed distribution, and can even provide conclusions for purely hypothetical scenarios. In this sense, discovering causal relationships means obtaining reliable knowledge that is not restricted by the observed data distribution and training tasks, thus providing an unambiguous specification for interpretable learning.
3. Three levels of causal learning modeling
Specifically, machine learning models based on statistical models can only model correlation relationships, while correlation Relationships tend to change with changes in data distribution; while causal models are based on causal relationship modeling, which captures the essence of data generation and reflects the relationship between data generation mechanisms. Such relationships are more robust and have the ability to generalize outside the distribution. ability. In decision theory, for example, the distinction between causation and statistics is clearer. There are two types of problems in decision theory. One is knowing the current environment, planning to intervene, and predicting the outcome. The other type is to know the current environment and results and infer the causes. The former is called the consequential problem, and the latter is called the abduction problem [3].
Predictive ability under independent and identically distributed conditions
Statistical models are only superficial descriptions of the observed real world because they only focus on correlations. For samples and labels, we can use estimates to answer questions like: "What is the probability that there is a dog in this particular photo?" "Given some symptoms, what is the probability of heart failure?". Such questions can be answered by observing enough generated i.i.d. data. Although machine learning algorithms can do these things well, accurate predictions are not enough for our decision-making, and causal learning provides a useful supplement. As for the previous example, the frequency of Nicolas Cage starring in movies is positively correlated with the drowning death rate in the United States. We can indeed train a statistical learning model to predict the drowning death rate in the United States based on the frequency of Nicolas Cage starring in movies, but obviously this There is no direct causal relationship between the two. Statistical models are only accurate when they are independently and identically distributed. If we make any intervention to change the data distribution, it will cause errors in the statistical learning model.
Predictive ability under distribution shift/intervention
We further discuss the intervention problem, which is more challenging because intervention (operation) will take us out of the independent and identically distributed in statistical learning. Assumption. Continuing with the Nicolas Cage example, “Will increasing the number of Nicolas Cage movies this year increase the drowning rate in the United States?” is an intervention question. Obviously, human intervention will cause the data distribution to change, and the conditions for statistical learning to survive will be broken, so it will fail. On the other hand, if we can learn a predictive model in the presence of an intervention, then this potentially allows us to get a model that is more robust to distributional changes in real-world settings. In fact, the so-called intervention here is nothing new. Many things themselves change over time, such as people's interest preferences, or there is a mismatch in the distribution of the model's training set and test set itself. As we have mentioned before, the robustness of neural networks has received more and more attention and has become a research topic closely connected with causal inference. Prediction in the case of distribution shift cannot be limited to achieving high accuracy on the test set. If we hope to use machine learning algorithms in practical applications, then we must believe that the prediction results of the model will also change when environmental conditions change. precise. The categories of distribution shifts in practical applications may be diverse. A model only achieves good results on some test sets does not mean that we can trust this model in any situation. These test sets may just fit these test sets. The distribution of the sample. In order for us to be able to trust predictive models in as many situations as possible, we must employ models that have the ability to answer intervention questions, at least not just using statistical learning models.
The ability to answer counterfactual questions
Counterfactual questions involve reasoning about why things happened, imagining the consequences of performing different actions, and from this, you can decide to take actions to achieve the desired results. Answering counterfactual questions is more difficult than intervention, but it is also a critical challenge for AI. If an intervention question is "What would happen to a patient's risk of heart failure if we started exercising regularly now?", the corresponding counterfactual question is "What if this patient who already had heart failure started exercising a year ago?" If he exercises, will he still get heart failure?" Obviously answering such counterfactual questions is very important for reinforcement learning. They can reflect on their own decisions, formulate counterfactual hypotheses, and then verify them through practice, just like our science Research is the same.
4. Causal Learning Application
Finally, let’s take a look at how to apply causal learning in various fields. The 2021 Nobel Prize in Economic Sciences was awarded to Joshua D. Angrist and Guido W. Imbens for their "methodological contributions to the analysis of causal relationships." They study the application of causal inference in empirical labor economics. The Nobel Prize in Economics selection committee believes that "natural experiments (randomized trials or controlled trials) can help answer important questions", but how to "use observational data to answer causal relationships" is more challenging. An important question in economics is the question of causation. For example, how do immigrants affect the labor market prospects of locals? Can studying for graduate school increase income? What impact does the minimum wage have on the employment prospects of skilled workers? These questions are difficult to answer because we lack the right means of interpreting counterfactuals.
Since the 1970s, statisticians have invented a framework for calculating “counterfactuals” to reveal the causal effect between two variables. On this basis, economists have further developed methods such as discontinuity regression, difference-in-differences, and propensity score, and have applied them extensively in causal research on various economic policy issues. From religious texts from the 6th century to causal machine learning in 2021, including causal natural language processing, we can use machine learning, statistics, and econometrics to model causal effects. Analysis in economics and other social sciences mainly revolves around the estimation of causal effects, that is, the intervention effect of a characteristic variable on the outcome variable. Actually, in most cases, the thing we're interested in is what's called the intervention effect. Intervention effect refers to the causal impact of an intervention or treatment on the outcome variable. For example, in economics, one of the most analyzed intervention effects is the causal impact of subsidies to companies on corporate income. To this end, Rubin proposed the potential outcome framework.
Although economists and other social scientists are better able to accurately estimate causal effects than to predict them, they are also interested in the predictive advantages of machine learning methods. For example, accurate sample prediction capabilities or the ability to handle large numbers of features. But as we have seen, classical machine learning models are not designed to estimate causal effects, and using off-the-shelf predictive methods from machine learning can lead to biased estimates of causal effects. Then, we must improve existing machine learning techniques to take advantage of machine learning to continuously and effectively estimate causal effects, which led to the birth of causal machine learning!
Currently, causal machine learning can be roughly divided into two research directions according to the type of causal effects to be estimated. An important direction is to improve machine learning methods for unbiased and consistent estimates of average intervention effects. Models in this area of research attempt to answer the following questions: What is the average customer response to a marketing campaign? What is the average impact of a price change on sales? Furthermore, another line of development in causal machine learning research is focused on improving machine learning methods to reveal the specificity of intervention effects, i.e., identifying subpopulations of individuals with greater or smaller than average intervention effects. This type of model aims to answer the following question: Which customers respond most to marketing campaigns? How does the impact of price changes on sales vary with customer age?
In addition to these living examples, we can also feel that a deeper reason why causal machine learning has attracted the interest of data scientists is the generalization ability of the model. Machine learning models that describe causal relationships between data can generalize to new environments, but this remains one of the biggest challenges in machine learning today.
Perl analyzes these issues at a deeper level and believes that if machines cannot reason causally, we will never achieve true human-level artificial intelligence, because causality is something we humans process and Understand the key mechanisms of the complex world around you. Pearl writes in the preface to the Chinese version of "On Causality" that "in the next decade, this framework will be combined with existing machine learning systems, potentially triggering a 'second causal revolution.' I hope this book It can also enable Chinese readers to actively participate in this upcoming revolution."
The above is the detailed content of Can machine learning really produce intelligent decisions?. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Bytedance Cutting launches SVIP super membership: 499 yuan for continuous annual subscription, providing a variety of AI functions
Jun 28, 2024 am 03:51 AM
Bytedance Cutting launches SVIP super membership: 499 yuan for continuous annual subscription, providing a variety of AI functions
Jun 28, 2024 am 03:51 AM
This site reported on June 27 that Jianying is a video editing software developed by FaceMeng Technology, a subsidiary of ByteDance. It relies on the Douyin platform and basically produces short video content for users of the platform. It is compatible with iOS, Android, and Windows. , MacOS and other operating systems. Jianying officially announced the upgrade of its membership system and launched a new SVIP, which includes a variety of AI black technologies, such as intelligent translation, intelligent highlighting, intelligent packaging, digital human synthesis, etc. In terms of price, the monthly fee for clipping SVIP is 79 yuan, the annual fee is 599 yuan (note on this site: equivalent to 49.9 yuan per month), the continuous monthly subscription is 59 yuan per month, and the continuous annual subscription is 499 yuan per year (equivalent to 41.6 yuan per month) . In addition, the cut official also stated that in order to improve the user experience, those who have subscribed to the original VIP
 Context-augmented AI coding assistant using Rag and Sem-Rag
Jun 10, 2024 am 11:08 AM
Context-augmented AI coding assistant using Rag and Sem-Rag
Jun 10, 2024 am 11:08 AM
Improve developer productivity, efficiency, and accuracy by incorporating retrieval-enhanced generation and semantic memory into AI coding assistants. Translated from EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG, author JanakiramMSV. While basic AI programming assistants are naturally helpful, they often fail to provide the most relevant and correct code suggestions because they rely on a general understanding of the software language and the most common patterns of writing software. The code generated by these coding assistants is suitable for solving the problems they are responsible for solving, but often does not conform to the coding standards, conventions and styles of the individual teams. This often results in suggestions that need to be modified or refined in order for the code to be accepted into the application
 Seven Cool GenAI & LLM Technical Interview Questions
Jun 07, 2024 am 10:06 AM
Seven Cool GenAI & LLM Technical Interview Questions
Jun 07, 2024 am 10:06 AM
To learn more about AIGC, please visit: 51CTOAI.x Community https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou is different from the traditional question bank that can be seen everywhere on the Internet. These questions It requires thinking outside the box. Large Language Models (LLMs) are increasingly important in the fields of data science, generative artificial intelligence (GenAI), and artificial intelligence. These complex algorithms enhance human skills and drive efficiency and innovation in many industries, becoming the key for companies to remain competitive. LLM has a wide range of applications. It can be used in fields such as natural language processing, text generation, speech recognition and recommendation systems. By learning from large amounts of data, LLM is able to generate text
 Can fine-tuning really allow LLM to learn new things: introducing new knowledge may make the model produce more hallucinations
Jun 11, 2024 pm 03:57 PM
Can fine-tuning really allow LLM to learn new things: introducing new knowledge may make the model produce more hallucinations
Jun 11, 2024 pm 03:57 PM
Large Language Models (LLMs) are trained on huge text databases, where they acquire large amounts of real-world knowledge. This knowledge is embedded into their parameters and can then be used when needed. The knowledge of these models is "reified" at the end of training. At the end of pre-training, the model actually stops learning. Align or fine-tune the model to learn how to leverage this knowledge and respond more naturally to user questions. But sometimes model knowledge is not enough, and although the model can access external content through RAG, it is considered beneficial to adapt the model to new domains through fine-tuning. This fine-tuning is performed using input from human annotators or other LLM creations, where the model encounters additional real-world knowledge and integrates it
 To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
Editor |ScienceAI Question Answering (QA) data set plays a vital role in promoting natural language processing (NLP) research. High-quality QA data sets can not only be used to fine-tune models, but also effectively evaluate the capabilities of large language models (LLM), especially the ability to understand and reason about scientific knowledge. Although there are currently many scientific QA data sets covering medicine, chemistry, biology and other fields, these data sets still have some shortcomings. First, the data form is relatively simple, most of which are multiple-choice questions. They are easy to evaluate, but limit the model's answer selection range and cannot fully test the model's ability to answer scientific questions. In contrast, open-ended Q&A
 SOTA performance, Xiamen multi-modal protein-ligand affinity prediction AI method, combines molecular surface information for the first time
Jul 17, 2024 pm 06:37 PM
SOTA performance, Xiamen multi-modal protein-ligand affinity prediction AI method, combines molecular surface information for the first time
Jul 17, 2024 pm 06:37 PM
Editor | KX In the field of drug research and development, accurately and effectively predicting the binding affinity of proteins and ligands is crucial for drug screening and optimization. However, current studies do not take into account the important role of molecular surface information in protein-ligand interactions. Based on this, researchers from Xiamen University proposed a novel multi-modal feature extraction (MFE) framework, which for the first time combines information on protein surface, 3D structure and sequence, and uses a cross-attention mechanism to compare different modalities. feature alignment. Experimental results demonstrate that this method achieves state-of-the-art performance in predicting protein-ligand binding affinities. Furthermore, ablation studies demonstrate the effectiveness and necessity of protein surface information and multimodal feature alignment within this framework. Related research begins with "S
 Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Machine learning is an important branch of artificial intelligence that gives computers the ability to learn from data and improve their capabilities without being explicitly programmed. Machine learning has a wide range of applications in various fields, from image recognition and natural language processing to recommendation systems and fraud detection, and it is changing the way we live. There are many different methods and theories in the field of machine learning, among which the five most influential methods are called the "Five Schools of Machine Learning". The five major schools are the symbolic school, the connectionist school, the evolutionary school, the Bayesian school and the analogy school. 1. Symbolism, also known as symbolism, emphasizes the use of symbols for logical reasoning and expression of knowledge. This school of thought believes that learning is a process of reverse deduction, through existing
 Laying out markets such as AI, GlobalFoundries acquires Tagore Technology's gallium nitride technology and related teams
Jul 15, 2024 pm 12:21 PM
Laying out markets such as AI, GlobalFoundries acquires Tagore Technology's gallium nitride technology and related teams
Jul 15, 2024 pm 12:21 PM
According to news from this website on July 5, GlobalFoundries issued a press release on July 1 this year, announcing the acquisition of Tagore Technology’s power gallium nitride (GaN) technology and intellectual property portfolio, hoping to expand its market share in automobiles and the Internet of Things. and artificial intelligence data center application areas to explore higher efficiency and better performance. As technologies such as generative AI continue to develop in the digital world, gallium nitride (GaN) has become a key solution for sustainable and efficient power management, especially in data centers. This website quoted the official announcement that during this acquisition, Tagore Technology’s engineering team will join GLOBALFOUNDRIES to further develop gallium nitride technology. G






