
Showing the Power of Neuro-Symbolic Programming
Over the past few years, we have seen Transformer-based models have emerged and have been successfully applied in many fields such as natural language processing or computer vision. In this article, we will explore a concise, interpretable and scalable way to express deep learning models, specifically Transformer, as a hybrid architecture, i.e. by combining deep learning with symbolic artificial intelligence. Therefore, we will implement the model in a Python neurosymbolic framework called PyNeuraLogic.
By combining symbolic representations with deep learning, we fill gaps in current deep learning models, such as out-of-the-box interpretability and missing inference techniques. Perhaps, increasing the number of parameters is not the most reasonable way to achieve these desired results, just as increasing the number of megapixels in a camera does not necessarily produce better photos.
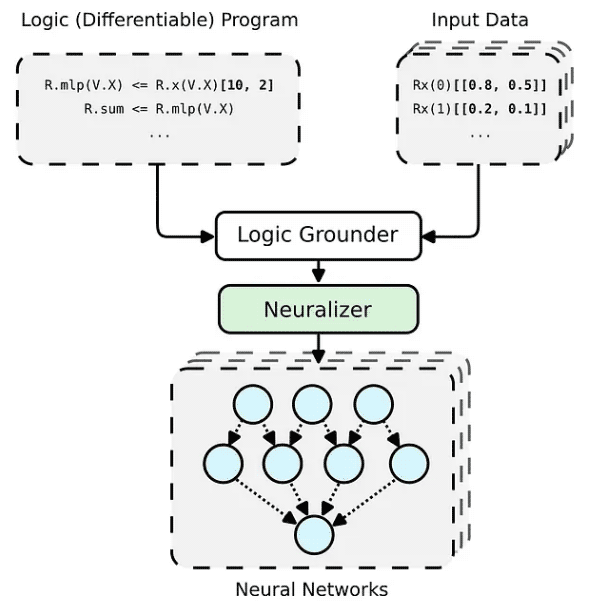
The PyNeuraLogic framework is based on logic programming - logic programs contain differentiable parameters. The framework is well suited for smaller structured data (such as molecules) and complex models (such as Transformers and graph neural networks). PyNeuraLogic is not the best choice for non-relational and large tensor data..
The key component of the framework is a differentiable logic program, which we call a template. A template consists of logical rules that define the structure of a neural network in an abstract way - we can think of a template as a blueprint for the model's architecture. The template is then applied to each input data instance to generate (through base and neuralization) a neural network that is unique to the input sample. Completely different from other predefined architectures, this process cannot adjust itself to different input samples.
#Normally, we will implement the deep learning model as tensor processing of batches of input tokens into a large tensor operate. This makes sense because deep learning frameworks and hardware (such as GPUs) are generally optimized for processing larger tensors rather than multiple tensors of different shapes and sizes. Transformers are no exception, typically batching a single token vector representation into a large matrix and representing the model as operations on such a matrix. However, such an implementation hides how individual input tokens relate to each other, as evidenced by the Transformer’s attention mechanism.
The attention mechanism forms the core of all Transformer models. Specifically, its classic version uses what is called multi-head scaling dot product attention. Let's use a header (for clarity) to decompose the scaled dot product attention into a simple logic program.
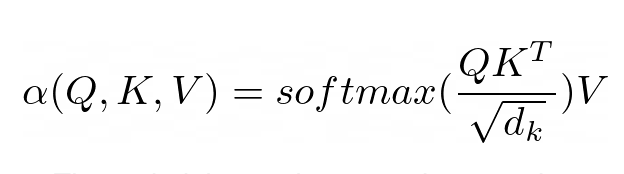
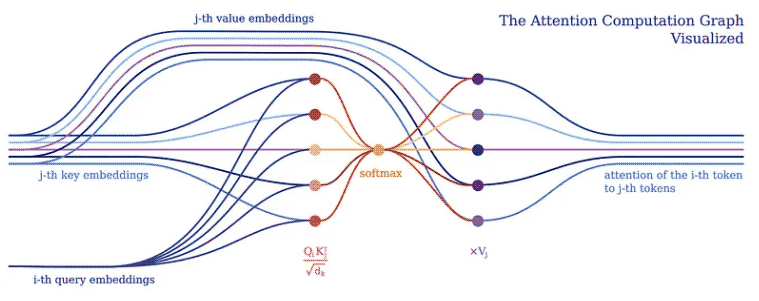
The purpose of attention is to decide which parts of the input the network should focus on. When implementing, attention should be paid to the weighted calculated value V. The weight represents the compatibility of the input key K and the query Q. In this particular version, the weights are calculated by the softmax function of the dot product of query Q and query key K, divided by the square root of the input feature vector dimension d_k.
(R.weights(V.I, V.J) <= (R.d_k, R.k(V.J).T, R.q(V.I))) | [F.product, F.softmax_agg(agg_terms=[V.J])], (R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.J)) | [F.product]
In PyNeuraLogic, we can fully capture the attention mechanism through the above logical rules. The first rule represents the calculation of the weight - it calculates the product of the inverse square root of the dimension and the transposed j-th key vector and i-th query vector. Next, we use the softmax function to aggregate the results of i with all possible j.
The second rule then computes the product between this weight vector and the corresponding j-th value vector, and sums the results for different j's for each i-th token.
During training and evaluation, we often limit what the input token can participate in. For example, we want to limit markers to look ahead and focus on upcoming words. Popular frameworks, such as PyTorch, achieve this by masking, i.e. setting a subset of elements of the scaled dot product result to some very low negative number. These numbers specify that the softmax function is forced to set the weight of the corresponding tag pair to zero.
(R.weights(V.I, V.J) <= (
R.d_k, R.k(V.J).T, R.q(V.I), R.special.leq(V.J, V.I)
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],We can easily achieve this by adding body relationship constraints to our symbols. We constrain the i-th indicator to be greater than or equal to the j-th indicator to calculate the weight. In contrast to masks, we only compute the required scaled dot product.
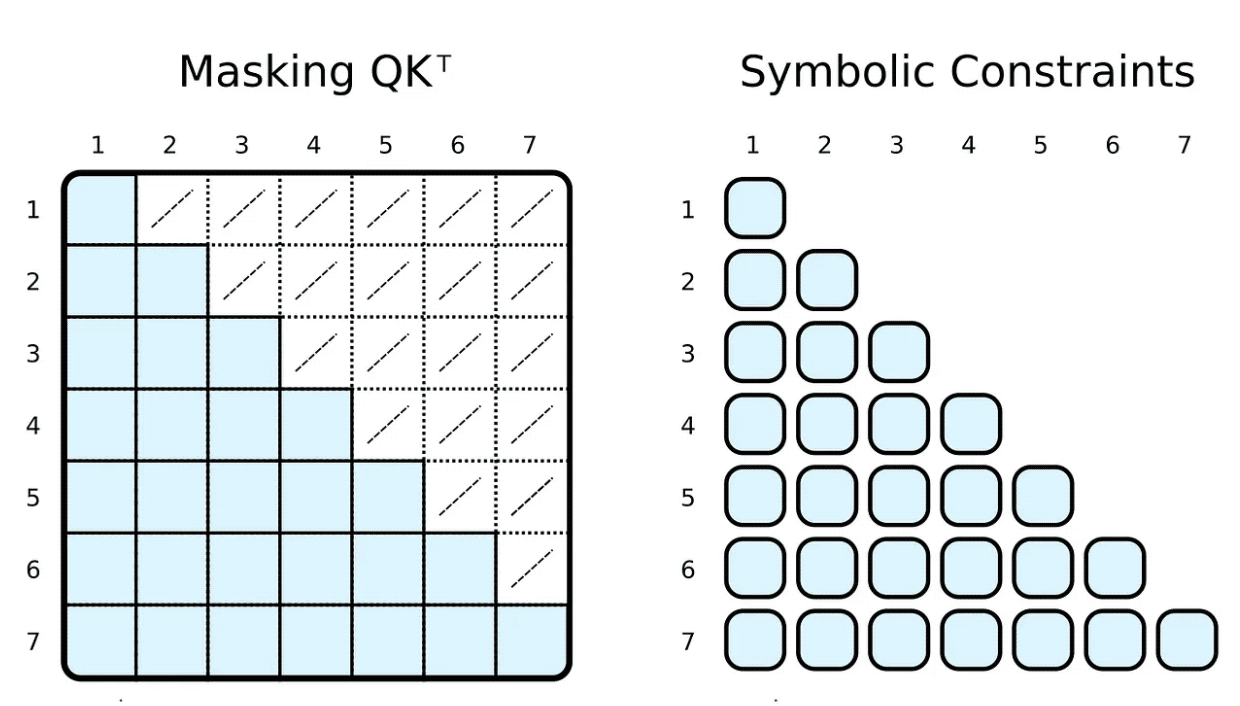
Of course, the symbolic "masking" can be completely arbitrary. Most people have heard of the sparse transformer-based GPT-3⁴, or its applications such as ChatGPT. ⁵ Attention (stride version) of the sparse transformer has two types of attention heads:
一个只关注前 n 个标记 (0 ≤ i − j ≤ n)
一个只关注每第 n 个前一个标记 ((i − j) % n = 0)
两种类型的头的实现都只需要微小的改变(例如,对于 n = 5)。
(R.weights(V.I, V.J) <= (
R.d_k, R.k(V.J).T, R.q(V.I),
R.special.leq(V.D, 5), R.special.sub(V.I, V.J, V.D),
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],(R.weights(V.I, V.J) <= (
R.d_k, R.k(V.J).T, R.q(V.I),
R.special.mod(V.D, 5, 0), R.special.sub(V.I, V.J, V.D),
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],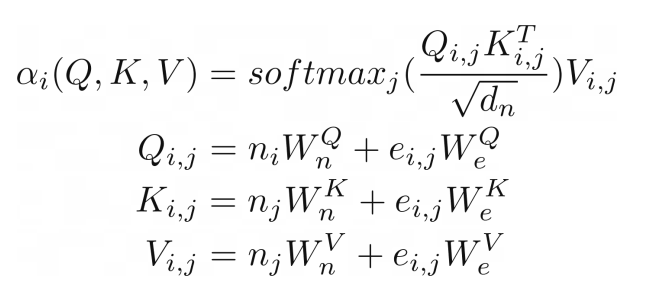
我们可以进一步推进,将类似图形输入的注意力概括到关系注意力的程度。⁶ 这种类型的注意力在图形上运行,其中节点只关注它们的邻居(由边连接的节点)。结果是节点向量嵌入和边嵌入的键 K、查询 Q 和值 V 相加。
(R.weights(V.I, V.J) <= (R.d_k, R.k(V.I, V.J).T, R.q(V.I, V.J))) | [F.product, F.softmax_agg(agg_terms=[V.J])], (R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.I, V.J)) | [F.product], R.q(V.I, V.J) <= (R.n(V.I)[W_qn], R.e(V.I, V.J)[W_qe]), R.k(V.I, V.J) <= (R.n(V.J)[W_kn], R.e(V.I, V.J)[W_ke]), R.v(V.I, V.J) <= (R.n(V.J)[W_vn], R.e(V.I, V.J)[W_ve]),
在我们的示例中,这种类型的注意力与之前展示的点积缩放注意力几乎相同。唯一的区别是添加了额外的术语来捕获边缘。将图作为注意力机制的输入似乎很自然,这并不奇怪,因为 Transformer 是一种图神经网络,作用于完全连接的图(未应用掩码时)。在传统的张量表示中,这并不是那么明显。
现在,当我们展示 Attention 机制的实现时,构建整个 transformer 编码器块的缺失部分相对简单。
如何在 Relational Attention 中实现嵌入已经为我们所展现。对于传统的 Transformer,嵌入将非常相似。我们将输入向量投影到三个嵌入向量中——键、查询和值。
R.q(V.I) <= R.input(V.I)[W_q], R.k(V.I) <= R.input(V.I)[W_k], R.v(V.I) <= R.input(V.I)[W_v],
查询嵌入通过跳过连接与注意力的输出相加。然后将生成的向量归一化并传递到多层感知器 (MLP)。
(R.norm1(V.I) <= (R.attention(V.I), R.q(V.I))) | [F.norm],
对于 MLP,我们将实现一个具有两个隐藏层的全连接神经网络,它可以优雅地表达为一个逻辑规则。
(R.mlp(V.I)[W_2] <= (R.norm(V.I)[W_1])) | [F.relu],
最后一个带有规范化的跳过连接与前一个相同。
(R.norm2(V.I) <= (R.mlp(V.I), R.norm1(V.I))) | [F.norm],
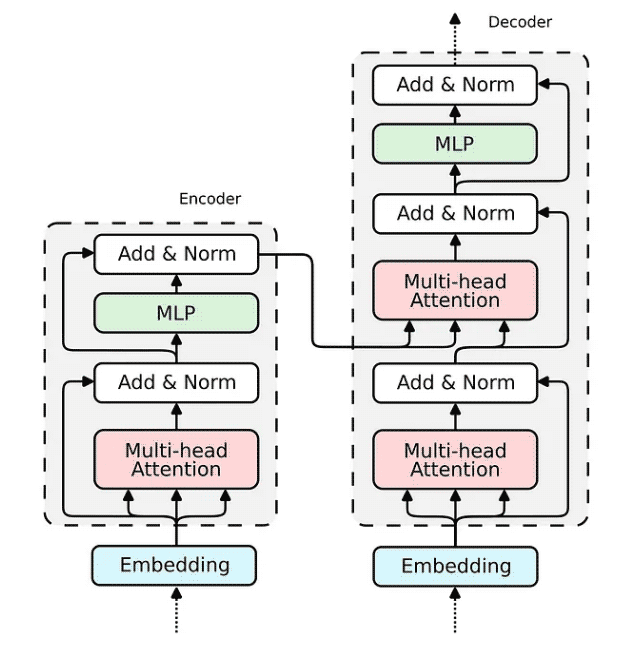
所有构建 Transformer 编码器所需的组件都已经被构建完成。解码器使用相同的组件;因此,其实施将是类似的。让我们将所有块组合成一个可微分逻辑程序,该程序可以嵌入到 Python 脚本中并使用 PyNeuraLogic 编译到神经网络中。
R.q(V.I) <= R.input(V.I)[W_q], R.k(V.I) <= R.input(V.I)[W_k], R.v(V.I) <= R.input(V.I)[W_v], R.d_k[1 / math.sqrt(embed_dim)], (R.weights(V.I, V.J) <= (R.d_k, R.k(V.J).T, R.q(V.I))) | [F.product, F.softmax_agg(agg_terms=[V.J])], (R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.J)) | [F.product], (R.norm1(V.I) <= (R.attention(V.I), R.q(V.I))) | [F.norm], (R.mlp(V.I)[W_2] <= (R.norm(V.I)[W_1])) | [F.relu], (R.norm2(V.I) <= (R.mlp(V.I), R.norm1(V.I))) | [F.norm],
The above is the detailed content of Python architecture PyNeuraLogic source code analysis. For more information, please follow other related articles on the PHP Chinese website!




