Implementation method of backtracking algorithm in PHP
Backtracking algorithm implementation method in PHP
Backtracking algorithm is a commonly used method to solve problems. Its core idea is to try all possible solutions recursively, and then proceed according to the requirements of the problem. Filter to find the optimal solution that meets the conditions.
In PHP, we can use the backtracking algorithm to solve a series of problems such as combination problems, permutation problems, mazes, etc. Below we will introduce how to implement the backtracking algorithm in PHP and give code examples.
- Backtracking algorithm implementation of combinatorial problem
The combinatorial problem refers to selecting several elements from a given set so that the selected elements meet specific conditions. Take the combination C(n, k) as an example, where n represents the size of the given set and k represents the number of elements to be selected. The following is an example of backtracking algorithm implementation in PHP to solve combinatorial problems:
function backtrack($nums, $k, $start, $track, &$res) {
if (count($track) == $k) {
$res[] = $track;
return;
}
for ($i = $start; $i < count($nums); $i++) {
$track[] = $nums[$i];
backtrack($nums, $k, $i + 1, $track, $res);
array_pop($track);
}
}
function combine($n, $k) {
$nums = [];
for ($i = 1; $i <= $n; $i++) {
$nums[] = $i;
}
$res = [];
backtrack($nums, $k, 0, [], $res);
return $res;
}
$n = 4;
$k = 2;
$result = combine($n, $k);
print_r($result);In the above code, the backtrack function is used to perform backtracking searches. When the number of selected elements is equal to k, we record the current track into the result array $res. Then make a recursive call in the for loop. The parameters passed in are the given set $nums, the number of elements to be selected $k, the currently selected starting position $start, the currently selected element array $track, and Result array $res.
- Backtracking algorithm implementation of permutation problem
The permutation problem refers to selecting a corresponding number of elements from a given set so that the selected elements are arranged in the order Meet certain conditions. Take the arrangement P(n, k) as an example, where n represents the size of the given set and k represents the number of elements to be selected. The following is an example of the implementation of the backtracking algorithm in PHP to solve the permutation problem:
function backtrack($nums, $k, &$visited, $track, &$res) {
if (count($track) == $k) {
$res[] = $track;
return;
}
for ($i = 0; $i < count($nums); $i++) {
if (!$visited[$i]) {
$visited[$i] = true;
$track[] = $nums[$i];
backtrack($nums, $k, $visited, $track, $res);
array_pop($track);
$visited[$i] = false;
}
}
}
function permute($nums, $k) {
$res = [];
$visited = array_fill(0, count($nums), false);
backtrack($nums, $k, $visited, [], $res);
return $res;
}
$nums = [1, 2, 3];
$k = 2;
$result = permute($nums, $k);
print_r($result);In the above code, the backtrack function is used to perform backtracking searches. When the number of selected elements is equal to k, we record the current track into the result array $res. In the for loop, we select an unvisited element each time and add it to the track. Then make a recursive call. The parameters passed in are the given set $nums, the number of elements to be selected $k, the array $visited that records whether the current element has been visited, the currently selected element array $track, and the result array. $res.
- Backtracking algorithm implementation of the maze problem
The maze problem refers to finding the path from the starting point to the end point in a given maze. A maze can be represented by a two-dimensional array, where 0 represents a passable grid and 1 represents an obstacle. The following is an example of the implementation of the backtracking algorithm to solve the maze problem in PHP:
function backtrack($maze, $i, $j, $path, &$res) {
if ($i == count($maze) - 1 && $j == count($maze[0]) - 1) {
$res[] = $path;
return;
}
$maze[$i][$j] = -1;
$dirs = [[0, 1], [1, 0], [0, -1], [-1, 0]];
$dirNames = ['right', 'down', 'left', 'up'];
for ($k = 0; $k < 4; $k++) {
$ni = $i + $dirs[$k][0];
$nj = $j + $dirs[$k][1];
if ($ni >= 0 && $ni < count($maze) && $nj >= 0 && $nj < count($maze[0]) && $maze[$ni][$nj] == 0) {
backtrack($maze, $ni, $nj, $path . ' -> ' . $dirNames[$k], $res);
}
}
$maze[$i][$j] = 0;
}
function solveMaze($maze) {
$res = [];
backtrack($maze, 0, 0, '(0, 0)', $res);
return $res;
}
$maze = [
[0, 1, 0, 0],
[0, 0, 0, 1],
[1, 1, 0, 0],
[0, 0, 0, 0]
];
$result = solveMaze($maze);
print_r($result);In the above code, the backtrack function is used to perform backtracking searches. When we reach the end point, we record the current path path into the result array $res. In the for loop, we try to move forward in four directions: right, down, left, and up, and make recursive calls. Before the recursive call, we need to determine whether the current grid is a passable grid and mark it as inaccessible to avoid repeated visits.
The above is the detailed content of Implementation method of backtracking algorithm in PHP. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 CakePHP Project Configuration
Sep 10, 2024 pm 05:25 PM
CakePHP Project Configuration
Sep 10, 2024 pm 05:25 PM
In this chapter, we will understand the Environment Variables, General Configuration, Database Configuration and Email Configuration in CakePHP.
 PHP 8.4 Installation and Upgrade guide for Ubuntu and Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 Installation and Upgrade guide for Ubuntu and Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 brings several new features, security improvements, and performance improvements with healthy amounts of feature deprecations and removals. This guide explains how to install PHP 8.4 or upgrade to PHP 8.4 on Ubuntu, Debian, or their derivati
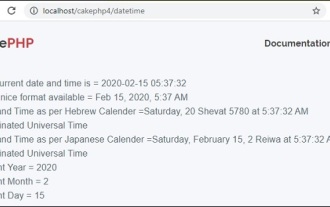 CakePHP Date and Time
Sep 10, 2024 pm 05:27 PM
CakePHP Date and Time
Sep 10, 2024 pm 05:27 PM
To work with date and time in cakephp4, we are going to make use of the available FrozenTime class.
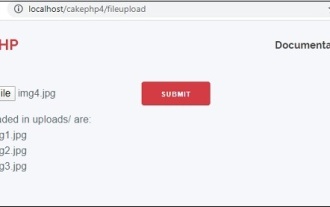 CakePHP File upload
Sep 10, 2024 pm 05:27 PM
CakePHP File upload
Sep 10, 2024 pm 05:27 PM
To work on file upload we are going to use the form helper. Here, is an example for file upload.
 Discuss CakePHP
Sep 10, 2024 pm 05:28 PM
Discuss CakePHP
Sep 10, 2024 pm 05:28 PM
CakePHP is an open-source framework for PHP. It is intended to make developing, deploying and maintaining applications much easier. CakePHP is based on a MVC-like architecture that is both powerful and easy to grasp. Models, Views, and Controllers gu
 CakePHP Routing
Sep 10, 2024 pm 05:25 PM
CakePHP Routing
Sep 10, 2024 pm 05:25 PM
In this chapter, we are going to learn the following topics related to routing ?
 CakePHP Working with Database
Sep 10, 2024 pm 05:25 PM
CakePHP Working with Database
Sep 10, 2024 pm 05:25 PM
Working with database in CakePHP is very easy. We will understand the CRUD (Create, Read, Update, Delete) operations in this chapter.
 CakePHP Creating Validators
Sep 10, 2024 pm 05:26 PM
CakePHP Creating Validators
Sep 10, 2024 pm 05:26 PM
Validator can be created by adding the following two lines in the controller.






